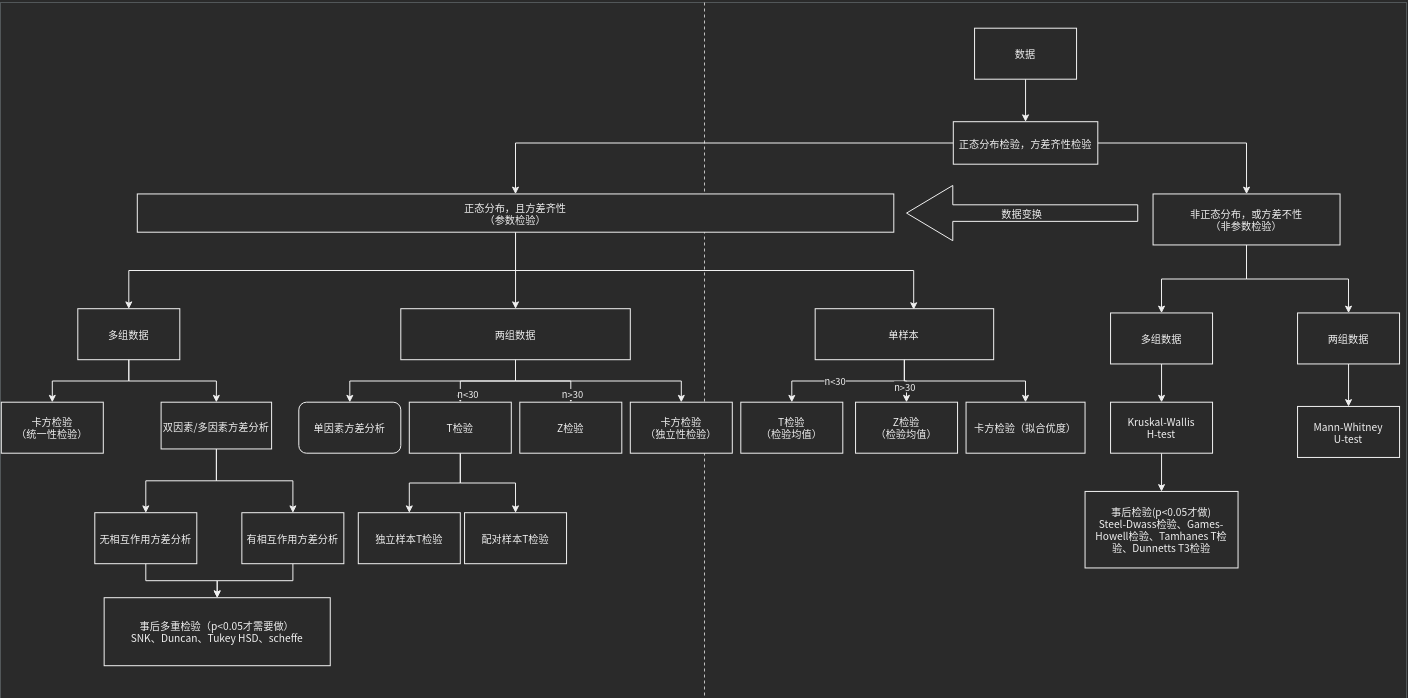
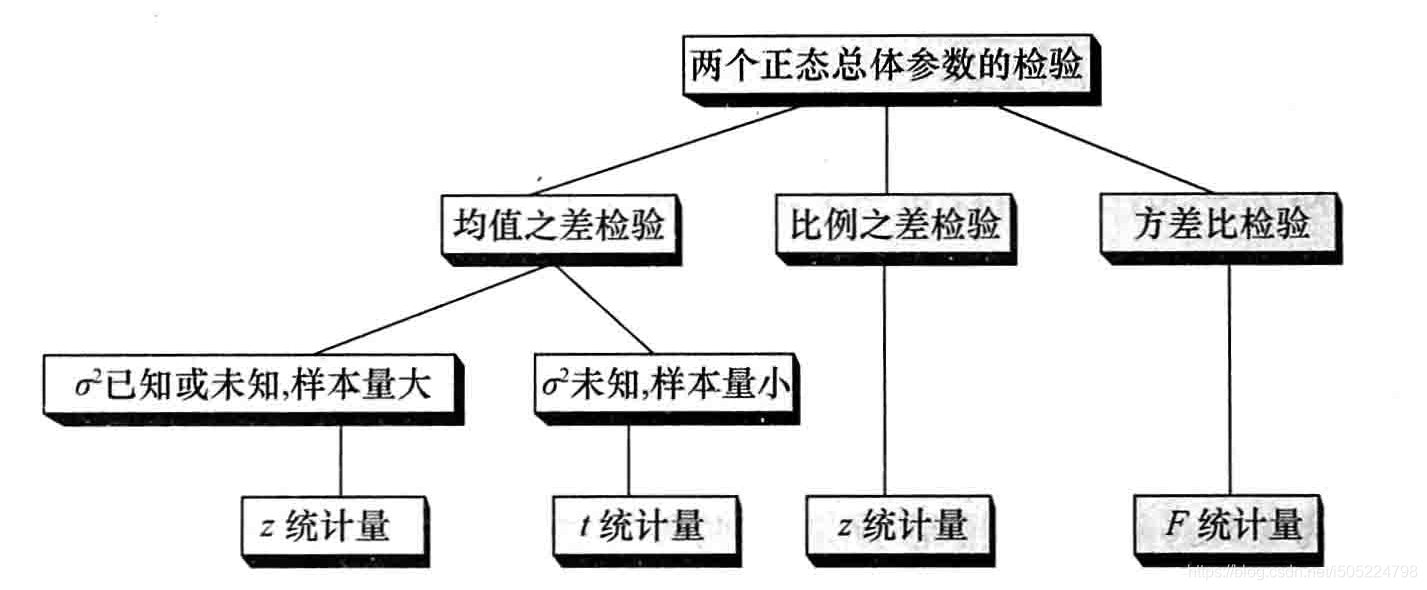
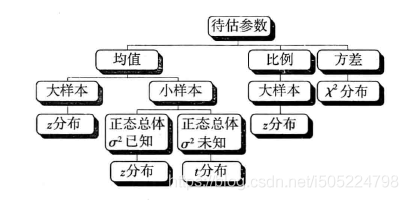
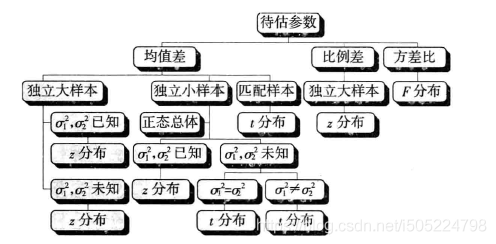
这里只将应用,不讲具体原理。原理查看前面假设检验的章节。
- 参数检验的集中趋势的衡量为均值,而非参数检验为中位数。
- 参数检验需要关于总体分布的信息;非参数检验不需要关于总体的信息。
- 参数检验只适用于变量,而非参数检验同时适用于变量和属性。
简而言之,若可以假定样本数据来自具有特定分布的总体,则使用参数检验。如果不能对数据集作出必要的假设,则使用非参数检验。
| F检验(方差齐性检验) | 研究X(定类)对于Y(定量)的差异 | |
|---|---|---|
测试数据
数据贯穿全文
from sklearn.datasets import load_irisiris = load_iris()#查看数据iris.data# 查看类别iris.target# Iris也称鸢尾花卉数据集,是一种多重变量分析的数据集。数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
正态性检验
决定了使用参数检验还是非参数检验。
检验方法(本文有):
| K-S检验 | Kolmogorov-Smirnov正态性检验法是检验单一样本是否来自某一特定分布 |
|---|---|
| S-W检验 | 大样本选择K-S检验;小样本选择S-W检验。 4000为阈值。 |
| AD检验 | |
| W检验 |
参数检验
F检验(又称方差齐性检验、方差比率检验)
方差齐性检验是对两组样本的方差是否相同进行检验。
研究X(定类)对于Y(定量)的差异时,方差齐用于判断X不同组别时Y的波动是否一致;
第一:分析方差齐检验是否呈现出显著性(p值小于0.05或0.01);
第二:如果没有呈现出显著性(p>0.05);直接使用方差分析对比差异;
第三:如果呈现出显著性(p<0.05);可考虑使用Welch anova,Brown-Forsythe anova,或者非参数检验研究差异关系;
第四:对分析进行总结。
应用:
- 方差齐性检验(F-test of equality of variances)
- 方差分析(Analysis of Variance, ANOVA)
- 线性回归方程整体的显著性检验
要点:
- 两组样本来自两个不同的正态分布总体
- 分别求出两组样本的样本均值和样本方差
- 原假设为两总体方差相等(这样引入F统计量后可以约掉总体方差)
引入F分布
约定较大的样本方差作分子,较小的样本方差做分母,这样计算出来 F>1,容易查表。
检验类型:
| 方差比 | 要求总体是正态分布 |
|---|---|
| Hartley检验 | 要求总体是正态分布 |
| Bartlett检验 | 要求总体是正态分布,适用于适用于多组方差 |
| Levene检验 | 不要求总体是正态分布,且适用于适用于多组方差 |
| BF法 | 不要求总体是正态分布 |
方差齐性检验案例:
from scipy.stats import bartlett,levenex = iris.data[:50,0]y = iris.data[50:100,0]z = iris.data[100:,0]# Bartlett检验# Bartlett检验的核心思想是通过求取不同组之间的卡方统计量,然后根据卡方统计量的值来判断组间方差是否相等。该方法极度依赖于数据是正态分布,如果数据非正态分布,则的出来的结果偏差很大。stat, p = bartlett(x,y,z)print(stat, p)# levene是一种特殊的方差分析(F检验),不过是用来进行方差齐性检验的。# Levene检验是将每个值先转换为为该值与其组内均值的偏离程度,然后再用转换后的偏离程度去做方差分析,即组间方差/组内方差。# 组内均值有多种计算方式:平均数、中位数、截取平均数(去掉最大和最小值后求平均)。stat, p = levene(x,y,z,center='median', proportiontocut=0.05)print(stat, p)>> 6.35272002048269 0.0022585277836218586stat是检验统计量,这里是F检验统计量p值小于0.05、0.001,说明出现显著性
方差分析
方差分析用于两个或两个以上样本均数差别的显著性检验。必须满足正态性检验和方差齐性检验。不满足则换成非参数检验。
方差分析是一种假设检验,它把观测总变异的平方和与自由度分解为对应不同变异来源的平方和与自由度,将某种控制性因素所导致的系统性误差和其他随机性误差进行对比,从而推断各组样本之间是否存在显著性差异,以分析该因素是否对总体存在显著性影响。
方差齐性是指不同组间的总体方差是一样的。而方差分析是用来比较多组之间均值是否存在显著差异。
如果组间方差不一致,也就意味着值的波动程度是不一样的,如果此时均值之间存在显著差异,不能够说明一定是不同组间处理带来的,有可能是大方差带来大的波动;如果方差一样,也就意味着值的波动程度是一样的,在相同波动程度下,直接去比较均值,如果均值之间存在显著差异,那么可以认为是不同组间处理带来的。
从理论上讲,方差分析有两个前提条件,一是因变量Y需要满足正态性要求,二是满足方差齐检验。如果不满足,此时可使用非参数检验进行研究差异性。也有文献提及可将数据进行转换后使其更加接近或符合正态性,然后继续使用方差分析,可尝试进行数据转换,一般是对数据进行比如求对数,开根号等处理。理论上的正态分布并不存在,数据接近于正态分布更符合实际情况,因此接近正态分布的数据直接使用方差分析即可。
单因素方差分析(one-way ANOVA)
单因素方差分析,用于分析定类数据(X)与定量数据(Y)之间的差异关系情况,比如不同学历人群对满意度差异关系。
在使用单因素方差分析时,需要每个选项的样本量大于30,比如男性和女性样本量分别是100和120,如果出现某个选项样本量过少时应该首先进行组别合并处理,比如研究不同年龄组样本对于研究变量的差异性态度时,年龄小于20岁的样本量仅为20个,那么需要将小于20岁的选项与另外一组(比如20~25岁)的组别合并为一组,然后再进行单因素方差分析。
如果选项无法进行合并处理,比如研究不同专业样本对于变量的态度差异,研究样本的专业共分为市场营销、心理学、教育学和管理学四个专业,这四个专业之间为彼此独立无法进行合并组别,但是市场营销专业样本量仅为20并没有代表意义,因此可以考虑首先筛选出市场营销专业,即仅比较心理学,教育学和管理学这三个专业对某变量的差异性态度,当对比的组别超过三个,并且呈现出显著性差异时,可以考虑使用事后检验进一步对比具体两两组别间的差异情况。
案例:
鸢尾花卉数据集中,研究不同种类的花卉(定类)对花萼长度(定量)差异关系。那么,花萼长度就是试验指标,影响试验指标的条件称为因素。现在只有一个因素,因此为单因素。单因素有3个不同种类,称为3个不同水平。在每个水平下,要考察的指标可以看成一个总体,那么就有3个不同总体。
前置条件:
- 每个总体均服从正态分布(此处要用正态性检验,每个总体各做一次,共三次)
- 每个总体的方差相同(此处要用方差齐性检验)
这里实现时,为了节省空间,直接跳过正态性检验和方差齐性检验,假设都满足。
这里的实现用了线性回归,原因参考单因素方差分析与线性回归的关系
原假设:总体均值都相等
import pandas as pdimport statsmodels.api as smfrom statsmodels.formula.api import olscalyxLength = [float(i) for i in iris.data[:,0]]labels = [str(i) for i in iris.target]df = pd.DataFrame({'labels':labels,"calyxLength":calyxLength})mod = ols('calyxLength ~ labels', data=df).fit()ano_table = sm.stats.anova_lm(mod, typ=1)print(ano_table)>>df sum_sq mean_sq F PR(>F)labels 2.0 63.212133 31.606067 119.264502 1.669669e-31Residual 147.0 38.956200 0.265008 NaN NaN# 首列是误差来源,依次为组间因素影响、组间随机影响# df 是自由度:依次为k-1、n-k# sum_sq:平方和,依次为SSA(因素误差平方和)、SSE(随机误差平方和),它们的和为SST(总误差平方和)# mean_sq:sum_sq的均方,依次记为MSA、MSE# F:F统计量, F=MSA/MSE~F(k-1,n-k)#PR(>F): p值
参数解释:
- ano_table = sm.stats.anova_lm(mod, typ=1) 中的typ=1为I 型单因素方差分析(type I ANOVA),是日常所需要的,此外还有II 型和III 型,可以参考什么是I,II,III型单因素方差分析
# 查看回归的报告print(mod.summary())
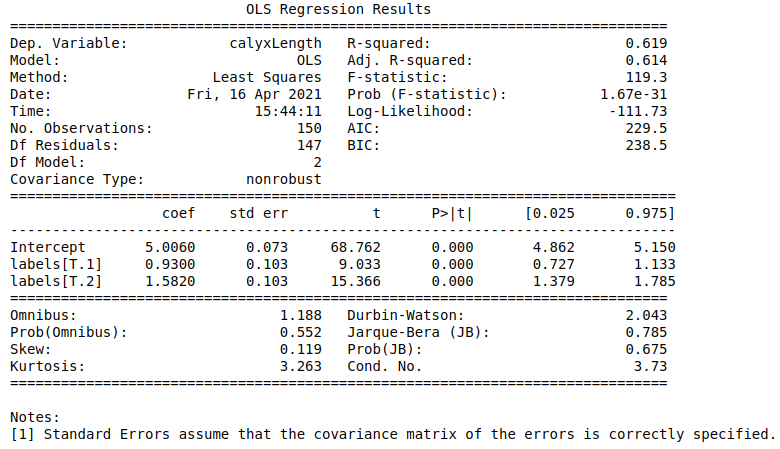
从报告中可以看出,p<0.05,拒绝原假设。说明不同类别间的数据存在显著差异。但是,具体哪个类别之间存在差异还需要通过多重检验。可能会得到某几个类别对未通过多重检验的类别,根据均值分布图直观看出相近的类别是否就是未通过多重检验的类别对,此时可以大胆按照类别对合并两个类别为一个类别,再做一次单因素方差分析。双因素方差分析(Two-way ANOVA)
对应到机器学习类似多类分类。
在现实中,常常会遇到两个因素同时影响结果的情况。这就需要检验究竟一个因素起作用,还是两个因素都起作用,或者两个因素的影响都不显著。
双因素方差分析有两种类型:一个是无交互作用的双因素方差分析,它假定因素A和因素B的效应之间是相互独立的,不存在相互关系;另一个是有交互作用的双因素方差分析,它假定因素A和因素B的结合会产生出一种新的效应。这种效应的最典型的例子是, 耕地深度和施肥量都会影响产量,但同时深耕和适当的施肥可能使产量成倍增加,这时,耕地深度和施肥量就存在交互作用。两个因素结合后就会产生出一个新的效应,属于有交互作用的方差分析问题。否则,就是无交互作用的背景。这里介绍无交互作用的双因素方差分析。
无交互作用的双因素方差分析
无交互作用的双因素方差分析,用于分析定类数据(2个)与定量数据之间的关系情况,例如研究人员性别,学历对于网购满意度的差异性;以及男性或者女性时,不同学历是否有着网购满意度差异性;或者同一学历时,不同性别是否有着网购满意度差异性。
案例:
考虑三种不同形式的广告和五种不同的价格对某种商品销量的影响。
我们先来看看无交互作用的双因素方差分析具体做法,所谓的无交互也就是假设价格和广告之间是没有交互作用的,相互不影响,只是彼此单独对销量产生影响。
在单因素方差分析中,我们是用F值去检验显著性的,多因素方差分析也同样是用F值。
| B1 | B2 | B3 | B4 | B5 | |
|---|---|---|---|---|---|
| A1 | 276 | 352 | 178 | 295 | 273 |
| A2 | 114 | 176 | 102 | 155 | 128 |
| A3 | 364 | 547 | 288 | 382 | 378 |
因素A为广告,因素B为价格,观测值为销量。直接上代码:
import numpy as npimport pandas as pdfrom statsmodels.formula.api import olsfrom statsmodels.stats.anova import anova_lmd = np.array([[276, 352, 178, 295, 273],[114, 176, 102, 155, 128],[364, 547, 288, 392, 378]])df = pd.DataFrame(d)df.index=pd.Index(['A1','A2','A3'],name='ad')df.columns=pd.Index(['B1','B2','B3','B4','B5'], name='price')df1 = df.stack().reset_index().rename(columns={0:'value'}) # 很重要,可以打印出来看,表达了A和B的位置关系mod = ols('value~C(ad) + C(price)', df1).fit()ano_table = anova_lm(mod,typ=1)print(ano_table)>>df sum_sq mean_sq F PR(>F)C(ad) 2.0 167804.133333 83902.066667 63.089004 0.000013C(price) 4.0 44568.400000 11142.100000 8.378149 0.005833Residual 8.0 10639.200000 1329.900000 NaN NaN
由于广告的p值 = 0.000 < 0.05,价格的 值 = 0.006 < 0.05,即可认为不同的广告形式、不同的价格均造成商品销量的显著差异。
有交互作用的双因素方差分析
直接对比交互作用的双因素方差分析的表格,可以发现同一个单元格中会含有多个值:
| B1 | B2 | B3 | |
|---|---|---|---|
| A1 | 58.2, 52.6 | 56.2, 41.2 | 65.3, 60.8 |
| A2 | 49.1, 42.8 | 54.1, 50.5 | 51.6, 48.4 |
| A3 | 60.1, 58.3 | 70.9, 73.2 | 39.2, 40.7 |
| A4 | 75.8, 71.5 | 58.2, 51.0 | 48.7, 41.4 |
火箭的射程与燃料的种类和推进器的型号有关,现对四种不同的燃料与三种不同型号的推进器进行试验,每种组合各发射火箭两次,测得火箭的射程结果如下(设显著性水平为0.01),这里火箭的射程不仅受到燃料类型和推进器型号的影响,同时还受到二者交互作用。直接上代码:
import numpy as npimport pandas as pdfrom statsmodels.formula.api import olsfrom statsmodels.stats.anova import anova_lmd = np.array([[58.2, 52.6, 56.2, 41.2, 65.3, 60.8],[49.1, 42.8, 54.1, 50.5, 51.6, 48.4],[60.1, 58.3, 70.9, 73.2, 39.2, 40.7],[75.8, 71.5, 58.2, 51.0, 48.7,41.4]])df = pd.DataFrame(d)df.index=pd.Index(['A1','A2','A3','A4'],name='燃料')df.columns=pd.Index(['B1','B1','B2','B2','B3','B3'],name='推进器')df1 = df.stack().reset_index().rename(columns={0:'射程'})mod = ols('射程~C(燃料) + C(推进器)+C(燃料):C(推进器)', df1).fit() # 关键点ano_table=anova_lm(mod)print(ano_table)>>df sum_sq mean_sq F PR(>F)C(燃料) 3.0 261.675000 87.225000 4.417388 0.025969C(推进器) 2.0 370.980833 185.490417 9.393902 0.003506C(燃料):C(推进器) 6.0 1768.692500 294.782083 14.928825 0.000062Residual 12.0 236.950000 19.745833 NaN NaN
对燃料因素来说,其p = 0.025大于显著性水平α = 0.01. 所以其对射程没有影响;
对推进器因素来说,其p = 0.003506小于显著水平α = 0.01, 所以其对射程影响显著。
对燃料和推进器的交互因素来说,其p = 0.000062小于显著水平α = 0.01,所以其对射程影响显著。
多因素方差分析
多因素方差分析通常用于类实验式问卷研究。比如研究者测试某新药对于胆固醇水平是否有疗效;研究者共招募72名被试,男女分别为36名,以及男女分别再细分使用新药和普通药物;同时高血压患者对于新药可能有干扰,因而研究者将被试是否患高血压也纳入考虑范畴中。因而最终,X共分为三个,分别是药物(旧药和新药)、性别,是否患高血压;Y为胆固醇水平。因而需要进行三因素方差分析即多因素方差分析。
事后多重检验/比较方法(有各种相近的描述。。。)
为什么方差分析一定要进行事后多重比较呢?直接用独立样本T检验进行多次两两比较不是也可以吗?我们可以用一个例子说明这个原因:以方差分析为例,假如有5个样本,如果要进行多次均值的两两比较,那么两两比较的次数多达10次。设每次比较的显著性水平等于0.05,那么10次比较都不犯“弃真”错误的概率为(1-0.05)的十次方,也就是0.60左右,也就是说犯“弃真”错误的概率高达0.40,这远远大于原先设定的显著性水平0.05。不仅如此,随着比较组数的增多,犯“弃真”错误的概率也会越来越大。
引用单因素方差分析的例子,进一步说明。
可用方法很多,但还是分为参数事后检验和非参数事后检验。
这里结合单因素方差分析的例子用一个参数事后检验(Tukey)来实验:
from statsmodels.stats.multicomp import MultiComparisonmc = MultiComparison(df['calyxLength'], df['labels'])tukey_result = mc.tukeyhsd(alpha = 0.5)print(tukey_result)>>Multiple Comparison of Means - Tukey HSD, FWER=0.50=================================================group1 group2 meandiff p-adj lower upper reject-------------------------------------------------0 1 0.93 0.001 0.8139 1.0461 True0 2 1.582 0.001 1.4659 1.6981 True1 2 0.652 0.001 0.5359 0.7681 True-------------------------------------------------
多重检验结果表明各个组间均存在显著差异(reject这一列为True的话则说明两个处理间存在差异)
其他检验类型(前提要求方差齐性):
| LSD | 最小显著性差异法(Least Significance Difference),是最简单的比较方法之一。它是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误(注意不是标准差)的计算上充分考虑了所有总体水平的样本信息,估计出了一个更为稳健的标准误。因为单次比较的显著性水平a保持不变,所以LSD法是最灵敏的事后多重比较法。 |
|---|---|
| Sidak | Sidak校正在LSD法上的应用。通过Sidak校正降低每次两两比较的“弃真”错误概率,以使最终整个比较的“弃真”错误概率保持为显著性水平a。这也就是说每次比较的显著性水平a会随着比较次数的增多而减小。显然,Sidak法比LSD法的灵敏度低。 |
| Bonferroni | 与Sidak法类似,它的每一次比较实际上是Bonferroni校正在LSD法上的应用。Bonferroni法修正后每次比较的显著性水平比Sidak法的更小,也就是说Bonferroni法比Sidak法的灵敏度更低。 |
| Scheffe | Scheffe法的实质是对多个总体均值间的线性组合是否为0进行假设检验。多用在两组样本含量不同的情况。 |
| Dunnett | 常用于多个试验组与一个对照组间的比较。因此在指定Dunnett法时,还应当指定对照组。 |
| SNK | 全称为Student-Newman-Keuls法。它实质上是根据预先指定的准则将各组均值分为多个亚组,利用Studentized Range分布来进行假设检验,并根据所要检验的均值个数调整总的“弃真”错误概率不超过设定的显著性水平a。 |
| Tukey | 全称为Tukey’ s Honestly Significant Difference法。应用这种方法要求各组样本含量相同。它也是利用Studentized Range分布来进行各组均数间的比较,与SNK法不同地是,它控制所有比较中最大的“弃真”错误概率不超过设定的显著性水平a。 |
| Duncan | 其思路与SNK法相类似,只不过检验统计量服从的是Duncan’ s Multiple Range分布。 |
前5个是两两比较的方法,按照灵敏度从高到低排列的,LSD法>Sidak法>Bonferroni法>Scheffe法>Dunnett法。
后三个是形成同质亚组的方法。
除此之外,在各组样本方差不齐时,尽量不要在方差不齐时进行方差分析甚至两两比较,采用变量变换或者非参数检验往往更可靠。
Z检验
Z检验需要满足以下几个条件:
1.总体是正态分布
2.样本数量足够大(一般大于30即可)
3.总体方差(或标准差)已知
其中,条件1和条件3只需满足一个即可
以下实验默认数据满足正态分布。数据每类50个样本。
实现参考 :https://www.statsmodels.org/stable/generated/statsmodels.stats.weightstats.ztest.html
statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative=’two-sided’, usevar=’pooled’, ddof=1.0)
单样本Z检验
检测一种花的花萼长度均值是否等于 5, 该问题显然是一个双侧检验,由于样本个数大于 30,则使用 z 检验
from statsmodels.stats.weightstats import ztestztest(iris.data[:50,0], value=5)>> (0.12036212238318056, 0.9041962951772449)统计量为 0.12036212238318056, p值为 0.9041962951772449
在置信度 α = 0.05 时,由于 p 值大于 α,接受原假设,认为该样本的均值是 5。
若要检测该样本均值是否大于 5,即原假设 H0:μ > 5,备选假设为:μ ≤ 5 ,则我们需要在代码中增加一个参数 alternative=”smaller”:
from statsmodels.stats.weightstats import ztestztest(iris.data[:50,0], value=5,alternative="smaller")>> (0.12036212238318056, 0.5479018524113776)
检测结果的 p 值为 0.547,大于置信度 0.05,则接受原假设,认为样本均值大于5。
独立样本Z检验
检测两种不同的花的花萼长度均值是否相等。
from statsmodels.stats.weightstats import ztestztest(iris.data[:50,0], iris.data[50:100,0])>> (-10.52098626754911, 6.914595261207391e-26)显然两种花萼长度均值不相等。
T检验
相比于Z检验,适合用于小样本数据集(<30),模块都是双侧检验,如果要单侧检验则要自己做换算
应用条件
- 正态性:(单样本、独立样本、配对样本T检验都需要)
- 连续变量:(单样本、独立样本、配对样本T检验都需要)
- 独立性:(独立样本T检验要求)
- 方差齐性:(独立样本T检验要求)
单样本T检验
比如问卷某题项选项表示为1分代表非常不满意,2分代表比较不满意,3分代表一般,4分代表比较满意,5分代表非常满意,当想分析样本对此题项的态度是否有明显的倾向,比如明显高于3分或者明显低于3分时,即可以使用单样本T检验。单样本T检验是比较某个题项的平均得分是否与某数字(例子是与3进行对比)有着明显的差异,如果呈现出显著性差异,即说明明显该题项平均打分明显不等于3分。此分析方法在问卷研究中较少使用,平均得分是否明显不为3分可以很直观的看出,而不需要单独进行检验分析。
案例:
检测一种花的花萼长度均值是否等于 5, 该问题显然是一个双侧检验,由于样本个数小于 30,则使用 t 检验
import scipy.stats as stst.ttest_1samp(iris.data[:20,0], 5)>> Ttest_1sampResult(statistic=0.36650245751349864, pvalue=0.7180397709426043)
从结果可以看出,双侧检验的 p 值为 0.718, 大于置信度 0.05,因此接受原假设,认为样本的均值是5。
若是单侧检验中的左侧检验,则 p 值为0.718 / 2 = 0.359 ,若是右侧检验,则 p 值为 1 − 0.718 / 2 = 0.612。
独立样本T检验
独立样本T检验和单因素方差分析功能上基本一致,但是独立样本T检验只能比较两组选项的差异,比如男性和女性。相对来讲,独立样本T检验在实验比较时使用频率更高,尤其是生物、医学相关领域。针对问卷研究,如果比较的类别为两组,独立样本T检验和单因素方差分析均可实现,研究者自行选择使用即可。
案例:
两个样本相互独立,检测两个样本的均值是否相等,使用 ttest_ind 函数。
检测两种花的花萼长度均值是否相等。
import scipy.stats as stst.ttest_ind(iris.data[:20,0], iris.data[50:70,0], equal_var = False)>> Ttest_indResult(statistic=-5.686672595509077, pvalue=2.153258160674022e-06)
参数:equal_var:若为 true,表示两个样本由相同的方差;若为 false,表示两个样本的方差不同,使用合并方差。
配对样本T检验
独立样本T检验和配对样本T检验功能上都是比较差异,而且均是比较两个组别差异。但二者有着实质性区别,如果是比较不同性别,婚姻状况(已婚和未婚)样本对某变量的差异时,应该使用独立样本T检验。如果比较组别之间有配对关系时,只能使用配对样本T检验,配对关系是指类似实验组和对照组的这类关系。另外独立样本T检验两组样本个数可以不相等,而配对样本T检验的两组样本量需要完全相等。
案例:
若两个样本是匹配样本,使用函数 ttest_rel,它的语法更简单,只需在函数里输入两个样本的数组即可。假设是配对样本。
import scipy.stats as stst.ttest_rel(iris.data[:20,0], iris.data[50:70,0])>> Ttest_relResult(statistic=-5.261687581045428, pvalue=4.446187570285963e-05)
非参数检验
卡方检验
可以参考这个链接
卡方检验需要满足卡方分布(卡方分布并不是指总体的分布,是指卡方值的分布,卡方值是一个理论数;其次,卡方检验是对检验样本是否符合某理论分布,不是对总体的参数进行检验。因此认为卡方检验不是参数检验)
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。它在分类数据统计推断中的应用,包括:两个率或两个构成比比较的卡方检验;多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
卡方检验是以χ2分布为基础的一种常用假设检验方法,它的原假设H0是:观察频数与期望频数没有差别。
该检验的基本思想是:首先假设H0成立,基于此前提计算出χ2值,它表示观察值与理论值之间的偏离程度。
χ2大小含义类似方差值大小。方差表示波动情况,χ2表示差异大小,χ2越大则观察频数与期望频数越接近。
应用条件
适用于四格表应用条件:
1)随机样本数据。两个独立样本比较可以分以下3种情况:
(1)所有的理论数T≥5并且总样本量n≥40,用Pearson卡方进行检验。
(2)如果理论数T<5但T≥1,并且n≥40,用连续性校正的卡方进行检验。
(3)如果有理论数T<1或n<40,则用Fisher’s检验。
2)卡方检验的理论频数不能太小。
R×C表卡方检验应用条件(R×C:多行多列…):
(1)R×C表中理论数小于5的格子不能超过1/5;
(2)不能有小于1的理论数。如果实验中有不符合R×C表的卡方检验,可以通过增加样本数、列合并来实现。
拟合优度检验
实际执行多项式试验而得到的观察次数,与虚无假设的期望次数相比较,称为卡方拟合优度检验,即在于检验二者接近的程度,利用样本数据以检验总体分布是否为某一特定分布的统计方法。这里以掷骰子为例介绍拟合优度检验的方法。
假设掷一骰子120次,各点数共出现次数为a,b为各点数出现的期望值120×1/6=20
设置零假设H0:观察分布等于期望分布。
投掷结果如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 18 | 19 | 23 | 20 | 16 | 24 |
import scipy.stats as ssobs=[18,19,23,20,16,24] # 点数1~6exp=[20]*6#拒绝域 1%的显著水平,自由度5jjy=ss.chi2.isf(0.01,5)#卡方ss.chisquare(obs,f_exp=exp)>> Power_divergenceResult(statistic=2.3, pvalue=0.8062668698851285)p值>0.05,原假设成立
独立性检验
卡方独立性检验是用来检验两个属性间是否独立。一个变量作为行,另一个变量作为列。下面一例便是介绍卡方独立性检验的方法。
案例:某机构欲了解现在性别与收入是否有关,他们随机抽样500人,询问对此的看法,结果分为“有关、无关、不好说”三种答案,下表为数据。
| 性别 | 有关 | 无关 | 不知道 |
|---|---|---|---|
| 男 | 120 | 60 | 50 |
| 女 | 100 | 110 | 60 |
(1)零假设H0:性别与收入无关。
(2)确定自由度为(3-1)×(2-1)=2,选择显著水平α=0.05。
求解男女对收入与性别相关不同看法的期望次数,这里采用所在行列的合计值的乘积除以总计值来计算每一个期望值
import numpy as npfrom scipy.stats import chi2_contingencycontingency_table = np.array([[120,60,50], [100,110,60]])Chi2, P, degree_of_freedom, contingency_table = chi2_contingency(contingency_table)>>Chi = 14.324834017928646 卡方值P = 0.0007751786733191823 P值degree_of_freedom = 2 自由度contingency_table = array([[101.2, 78.2, 50.6], 期望次数[118.8, 91.8, 59.4]])
统一性检验
检验两个或两个以上总体的某一特性分布,也就是各“类别”的比例是否统一或相近,一般称为卡方统一性检验或者卡方同质性检验。
案例:某咨询公司想了解南京和北京的市民对最低生活保障的满意程度是否相同。他们从南京抽出600居民,北京抽取600居民,每个居民对满意程度(非常满意、满意、不满意、非常不满意)任选一种,且只能选一种。如下表所示
| 满意程度 | 北京 | 上海 |
|---|---|---|
| 非常满意 | 100 | 110 |
| 满意 | 150 | 160 |
| 不满意 | 180 | 170 |
| 非常不满意 | 170 | 160 |
(1)零假设H0:南京和北京居民对最低生活保障满意程度的比例相同。
(2)确定自由度为(4-1)×(2-1)=3,选择显著水平α=0.05。
(3)计算北京和南京不同满意程度的期望值
import numpy as npfrom scipy.stats import chi2_contingencycontingency_table = np.array([[100,110], [150,160],[180,170],[170,160]])Chi2, P, degree_of_freedom, contingency_table = chi2_contingency(contingency_table)>>Chi2 = 1.3875157100963553,P = 0.708463710032442,degree_of_freedom = 3,contingency_table = array([[105., 105.],[155., 155.],[175., 175.],[165., 165.]]))
K-S检验
from statsmodels.stats.diagnostic import kstest_normalksstat, p = kstest_normal(x, dist='norm', pvalmethod='table')>> (0.11485990669608126, 0.09683860719317593)from scipy.stats import kstestkstest(rvs=x , cdf= 'norm')>> KstestResult(statistic=0.999991460094529, pvalue=7.476238875146382e-254)rvs:待检验的数据cdf:检验方法,这里我们设置为‘norm’,即正态性检验alternative:默认为双尾检验,可以设置为‘less’或‘greater’作单尾检验em ...... 没弄明白两个模块的检测结果差距巨大的原因。。。如果p值低于某个阈值,例如 0.05,则我们可以否定样本来自正态分布的零假设。
S-W检验
与 kstest 不同,shapiro 是专门用来做正态性检验的模块注意:shapiro 不适合做样本数>4000的正态性检验,检验结果的P值可能不准确
from scipy.stats import shapiroshapiro(x)>> ShapiroResult(statistic=0.9776989221572876, pvalue=0.4595281183719635)
AD检验
Anderson-Darling测试来自特定分发的数据。
安德森·达林(Anderson-Darling)检验检验了零假设的假设,即样本是从遵循特定分布的总体中抽取的。 对于Anderson-Darling测试,临界值取决于要针对哪个分布进行测试。 此函数适用于正态分布,指数分布,逻辑分布或Gumbel(极值类型I)分布。
anderson 是修改版的 kstest,说是增强版也不为过。也可以做多种分布的检验,默认的检验时正态性检验。
from scipy.stats import andersonanderson(x,dist='norm')>> AndersonResult(statistic=0.4079859754958619,critical_values=array([0.538, 0.613, 0.736, 0.858, 1.021]),significance_level=array([15. , 10. , 5. , 2.5, 1. ]))anderson 有三个输出值,第一个为统计数,第二个为评判值,第三个为显著性水平, 评判值与显著性水平对应对于正态性检验,显著性水平为:15%, 10%, 5%, 2.5%, 1%