三、占优策略均衡和理性化

前面讲过了：纯策略纳什均衡，混合策略纳什均衡以及他们的求解方法。这节课“占优策略”指的是一种特殊的策略（包括混合策略），能够简化纳什均衡的求解，也引出“理性化”的过程，消去不可能出现在纳什均衡中的策略。

一、占优策略(Dominant Strategy)

1. 例子

在囚徒困境中，收益矩阵是这样的：

• 当玩家2选择confess的时候，玩家1选confess是最优的；
• 当玩家2选择don’t confess的时候，玩家1选confess是最优的；

可以发现，不管玩家2如何选择，玩家1选择(confess)都是最优的。那么，对于玩家1来说，confess这个策略就是占优策略。

2. 形式化定义

沿用策略式博弈的记号，定义：

1. 严格占优于：和是一个玩家的两种纯策略，若对于所有，，则称策略严格占优于
2. 弱占优于：和是一个玩家的两种纯策略，若对于所有，，且对于某些，，则称策略弱占优于
3. 严格占优策略：如果严格占优于玩家其他所有策略，则称是严格占优策略。
4. 弱占优策略：如果弱占优于玩家其他所有策略，则称是弱占优策略。

严格占优就是收益高于其他策略；弱占优就是收益不低于其他策略，且有时高于其他策略。

二、占优策略均衡

定义：每个玩家的占优策略（严格占优策略或弱占优策略）构成的博弈结果，称为占优策略均衡。
从定义可以看出，占优策略均衡属于纳什均衡。
性质：易求解，但可能不存在。

三、例：第二价格拍卖(维克里拍卖)

N个买家通过密封投标的方式竞价，出价最高的投标者获得被拍卖的商品，并支付第二高的出价。竞品对玩家的价值是，玩家的出价是。
玩家的收益：
定理：在第二价格拍卖中，对于任意玩家，策略是一个弱占优策略，即，是一个占优策略均衡。
证明：即需证明对于任意，，分情况讨论如下：

• 如果某人的竞价
  • 玩家若想竞拍成功，则的收益小于0，不如选的策略(收益为0)。
  • 玩家若竞拍不成功，收益为0，和的策略相同。

• 如果所有人的竞价

  • 玩家若竞拍成功，则收益大于0，收益取决于的最大值(第二价格)，因此，没有比更好的选择了
  • 竞拍不成功，收益为0，不如的策略

    四、被占优策略(Dominated Strategies)

• 严格占优于，称被严格占优。

• 弱占优于，称被弱占优。

  1. 消除被占优策略可以用来求解占优策略均衡(迭代)

  例：
  

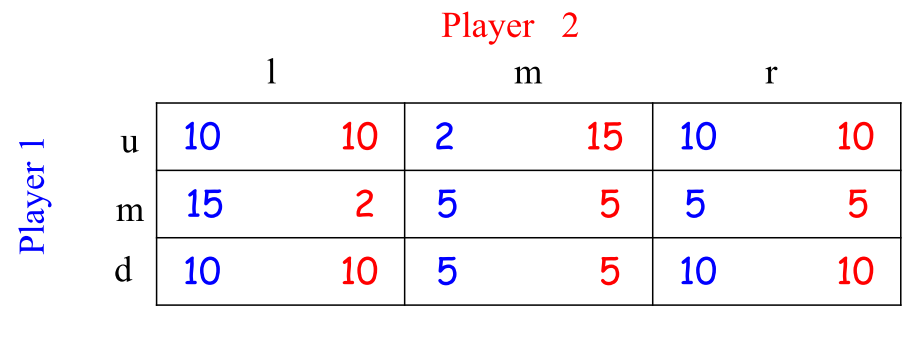
• 对于玩家1：‘u’策略被‘d’策略弱占优。

• 对于玩家2：‘l’策略被‘r’策略弱占优。

消除被占优策略‘u’和‘l’，得：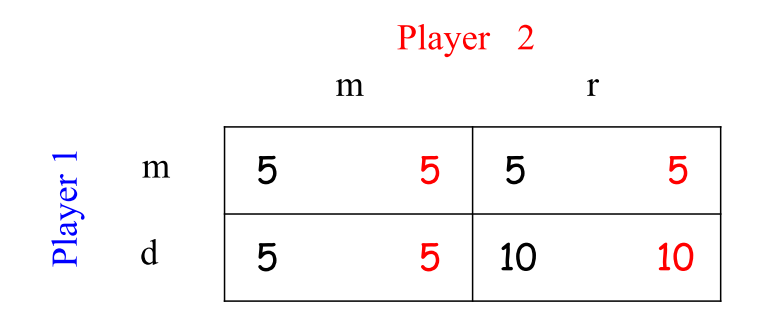

• 对于玩家1：‘m’策略被‘d’策略弱占优。
• 消去玩家1的‘m’策略后，对于玩家2：‘m’策略被‘r’策略严格占优。

最后，得到(d,r)是占优策略均衡(弱占优策略均衡)

2. 消除被占优策略可以用来简化混合策略纳什均衡(MNE)求解

一个策略可以被一个“混合策略”占优，如：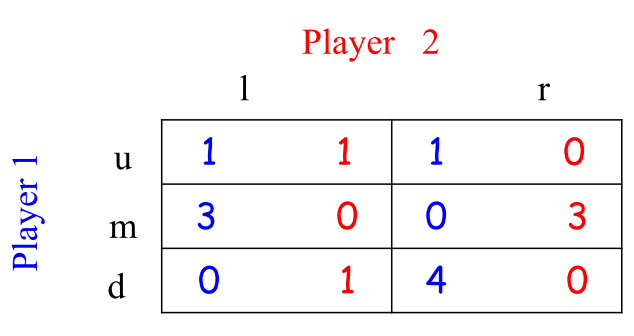

对于玩家1，没有纯策略能够占优于策略‘u’，但是不难看出混合策略严格占优于纯策略‘u’，更一般地，设玩家2的混合策略是，也就是以概率p选择l策略。
则玩家1在三种纯策略上的收益为：

画图如下：

可见，‘u’这个策略始终都不是最好的策略。

定理：被严格占优的策略在MNE中概率为0

证明：

• 笔记(二)MNE那一节讲过，每个具有正概率的纯策略都是的最优反应，也就是玩家选任意一种纯策略的期望收益是相同的。
• 但是，因为被严格占优，因此，因此，MNE中，的概率为0

利用这一定理，可以消去被严格占优的策略，简化MNE的求解。

五、信念和理性化

1. 信念(belief)

定义：“信念”的意思，就是认为对手会采用什么样的策略。对于混合策略博弈，博弈结果，其中，称为信念(belief)

2. 理性

纯策略是理性的，当：存在信念使得是的最优反应。
定理：在MNE中，每一个具有正概率的纯策略都是理性的。
定理：是理性的当且仅当不被严格占优。

3. 理性化

理性化：迭代消除被严格占优的策略直到没有被严格占优的策略。

六、例：选美比赛博弈(Beauty Contest game)

• n个玩家
• 每个人选[0,50]之间的一个数
• 玩家的收益是：，即与平均数的越接近，收益越高。

分析：
给定对手的策略，玩家的最优反应：

可以发现：

这时，在之间的策略都被严格占优，消去。
迭代理性化，第k次会得到区间：
一直迭代下去，最终得到结果：0
因此，纳什均衡是每个人的策略都是选0