梯度下降法、牛顿法和拟牛顿法

专栏文章汇总

本文结构如下

1：梯度下降法

• 1.1 梯度
• 1.2 梯度下降的直观解释
• 1.3 梯度下降算法法
• 1.4 梯度下降的算法调优
• 1.5 梯度下降法大家族（BGD，SGD，MBGD）
• 1.5.1 批量梯度下降法（Batch Gradient Descent）
• 1.5.2 随机梯度下降法（Stochastic Gradient Descent）
• 1.5.3 小批量梯度下降法（Mini-batch Gradient Descent）
• 1.6 批量梯度下降法 python 实现
• 1.7 梯度下降法和最小二乘法

2： 牛顿法

• 2.1 求解方程
• 2.2 最优化
• 2.3 牛顿法与梯度下降法

3： 拟牛顿法的思路

4： DFP(Davidon-Fletcher-Powell) 算法 (DFP algorithm)

5： BFGS(Broyden-Fletcher-Goldfard-Shano) 算法 (BFGS algorithm)

6： Broyden 类算法 (Broyden’s algorithm)

7： 参考文献

1： 梯度下降法

1.1 梯度

导数我们都非常熟悉，既可以表示某点的切线斜率，也可以表示某点变化率，公式如下表示：

当函数是多元时，倒数就变成了偏导数：
表示当
不变时，
沿着
轴的变化变化率；
表示当
不变时，
沿着
轴的变化变化率。

但是多元函数是一个平面，方向有很多，
轴
轴只是其中两个方向而已，假如我们需要其他方向的变化率怎么办呢？因此方向导数就有用了，顾名思义，方向导数可以表示任意方向的倒数。

假如二次函数
，方向
（为单位向量）的方向导数公式如下：
，记为
。其中
。我们记为：
，其中
是两向量的夹角。我们可以知道，当
为 0 时，方向导数
达到最大，此时的方向导数即为梯度。

更多的关于梯度的知识点可以看里面的回答：如何直观形象的理解方向导数与梯度以及它们之间的关系？

从几何意义上来说，梯度向量就是函数变化增加最快的地方。具体来说，对于函数
, 在点
，沿着梯度向量的方向就是
的方向是
增加最快的地方（还记得梯度怎么来的吗？方向导数的最大值，粗暴点，就是导数最大值）。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向（去负号），则就是更加容易找到函数的最小值。

1.2 梯度下降的直观解释

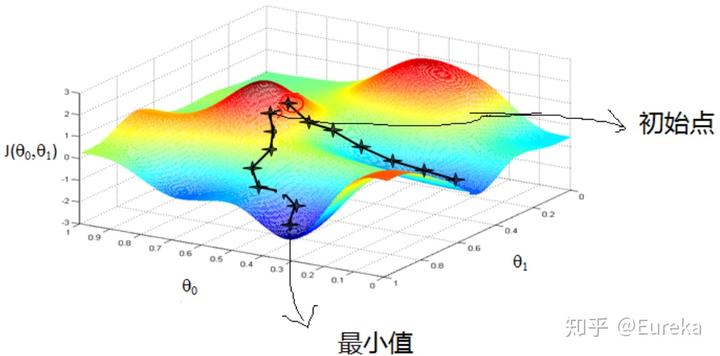
比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处（局部最小值）。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

1.3 梯度下降算法法

梯度下降法 (Gradient descent) 或最速下降法 (steepest descent) 是求解无约束最优化问题的一种常用的、实现简单的方法。

假设
是
上具有一阶连续偏导数的函数。求解

无约束最优化问题。
表示目标函数
的极小点。

梯度下降法是一种迭代算法。选取适当的初值
，不断迭代，更新
的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数下降最快的的方向，在迭代的每一步，以负梯度方向更新
的值，从而达到减少函数值的目的。

第
次迭代值

其中，
是搜索方向，取负梯度方向
是步长，由一维搜索确定，即
使得

梯度下降算法：
输入：目标函数
，梯度函数
，计算精度

输出：
的极小点

1. 取初值
   ，置

2. 计算

3. 计算梯度
   ，当
   时，停止迭代，令
   ；否则，令
   ，求
   ，使
   

4. 置
   ，计算

当
或
时，停止迭代，令

1. 否则，置
   ，转 3.

1.4 梯度下降的算法调优

在使用梯度下降时，需要进行调优。哪些地方需要调优呢？

1. 算法的步长选择。步长取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
3. 归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化。

1.5 梯度下降法大家族（BGD，SGD，MBGD）

1.5.1 批量梯度下降法（Batch Gradient Descent）
批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。

1.5.2 随机梯度下降法（Stochastic Gradient Descent）
随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的样本的数据，而是仅仅选取一个样本来求梯度。
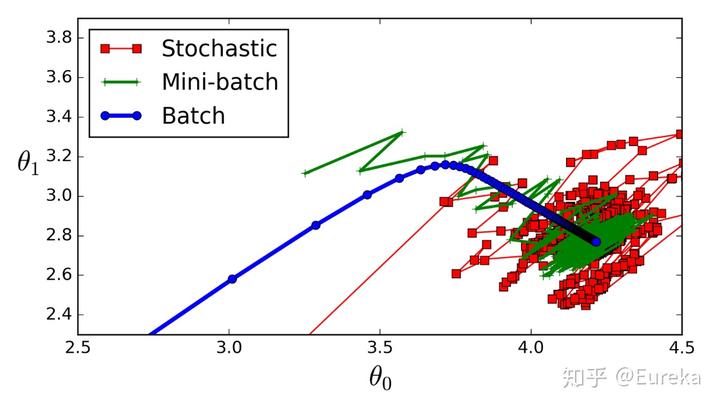
随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

1.5.3 小批量梯度下降法（Mini-batch Gradient Descent）
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于
个样本，我们采用
个样子来迭代，
。一般可以取
，当然根据样本的数据，可以调整这个
的值。

上述三种方法得到局部最优解的过程如下：

1.6 批量梯度下降法 python 实现

def train(X, y, W, B, alpha, max_iters):
    '''
    使用了所有的样本进行梯度下降
    X: 训练集,
    y: 标签,
    W: 权重向量,
    B: bias,
    alpha: 学习率,
    max_iters: 最大迭代次数.
    '''
    dW = 0 # 权重梯度收集器
    dB = 0 # Bias梯度的收集器
    m = X.shape[0] # 样本数
    for i in range(max_iters):
        dW = 0 # 每次迭代重置
        dB = 0
        for j in range(m):
            # 1. 迭代所有的样本
            # 2. 计算权重和bias的梯度保存在w_grad和b_grad,
            # 3. 通过增加w_grad和b_grad来更新dW和dB
            W = W - alpha * (dW / m) # 更新权重
            B = B - alpha * (dB / m) # 更新bias
    return W, B

1.7 梯度下降法和最小二乘法

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

2： 牛顿法

一般来说，牛顿法主要应用在两个方面，1：求方程的根；2：最优化。

2.1 求解方程

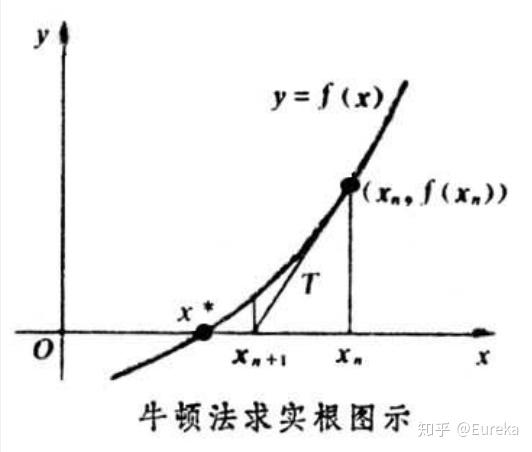
并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在
处展开，且展开到一阶, 即
。求解方程
，等价于
，求解
。因为这是利用泰勒公式的一阶展开，
处并不是完全相等，而是近似相等，这里求得的
并不能让
，只能说
的值比
的值更接近于 0，于是迭代的想法就很自然了，可以进而推出
，通过迭代，这个式子必然在
的时候收敛。整个过程如下：

2.2 最优化

无约束最优化问题

其中
为目标函数的极小点。

设
具有二阶连续偏导数，若第
次迭代值为
，则可将
在
附近进行二阶泰勒展开

其中，
是
的梯度向量在点
的值，
是
的海赛矩阵

在点
的值。

函数
有极值的必要条件是在极值点处一阶导数为 0，即梯度向量为 0。特别的当
是正定矩阵时，函数
的极值为极小值。

我们为了得到一阶导数为 0 的点，可以用到 2.1 里的求解方程方法。根据二阶泰勒展开，对
在
进行展开得（也可以对上述泰勒公式再进行求导）

其中，
，则

我们令

则得到迭代公式

最终可在
收敛。

牛顿法：
输入：目标函数
，梯度
，海赛矩阵
，精度要求

输出：
的极小点

1. 取初始点
   ，置

2. 计算

3. 若
   则停止计算，得近似解

4. 计算
   ，并求

1. 置

2. 置
   ，转 2.

2.3： 牛顿法与梯度下降法

梯度下降法和牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法是用二阶的海森矩阵的逆矩阵求解。相对而言，使用牛顿法收敛更快（迭代更少次数）。但是每次迭代的时间比梯度下降法长。

梯度下降法：

牛顿法：

如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

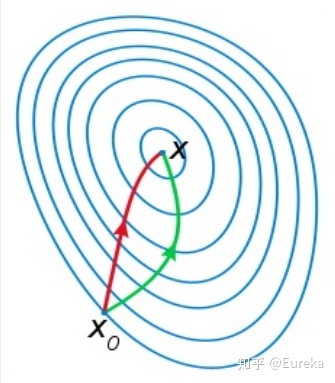
至于为什么牛顿法收敛更快，通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。更多的可见：最优化问题中，牛顿法为什么比梯度下降法求解需要的迭代次数更少？

3： 拟牛顿法的思路

在牛顿法的迭代中，需要计算海森矩阵的逆矩阵
，这一计算比较复杂，考虑用一个
阶矩阵
来近似代替
。这就是拟牛顿法的基本想法。

要找到近似的替代矩阵，必定要和
有类似的性质。先看下牛顿法迭代中海森矩阵
满足的条件。首先
满足以下关系：

取
，由

得

记
，则

称为拟牛顿条件 (Secant equation)。

注：在李航老师《统计机器学习》附录 B 中，取的是
，得到的拟牛顿条件是
，但是用
的到的拟牛顿条件和下面推导吻合，但还没找到原因，还望高手指教。

其次，如果
是正定的（
也是正定的），那么保证牛顿法的搜索方向
是下降方向。这是因为搜索方向是
，
由

有

则
在
的泰勒展开可近似为

由于
正定，故
。当
为一个充分小的正数时，有
，即搜索方向
是下降方向。

因此拟牛顿法将
作为
近似。要求
满足同样的条件。首先，每次迭代矩阵
是正定的。同时，
满足下面的拟牛顿条件：

按照拟牛顿条件，在每次迭代中可以选择更新矩阵
：

这种选择有一定的灵活性，因此有很多具体的实现方法，下面介绍 Broyden 类拟牛顿法。

4： DFP(Davidon-Fletcher-Powell) 算法 (DFP algorithm)

DFP 算法中选择
作为
的近似，假设每一步迭代中矩阵
是由
加上两个附加项构成，即

其中，
与
是待定矩阵。则

为使
满足拟牛顿条件，可使
与
满足

可取

可得矩阵
的迭代公式

可以证明，如果初始矩阵
是正定的，则迭代过程中的每个矩阵
都是正定的。

DFP 算法：
输入：目标函数
，梯度
，精度要求

输出：
的极小点

1. 取初始点
   ，取
   为正定矩阵，置

2. 计算
   ， 若
   则停止计算，得近似解
   ；否则，转 3.

3. 置

4. 一维搜索，求
   使
   

5. 置

6. 计算
   ，若
   则停止计算，近似解
   ；否则，计算
   

7. 置
   ，转 3.

5： BFGS(Broyden-Fletcher-Goldfard-Shano) 算法 (BFGS algorithm)

DFP 是用
逼近海赛矩阵的逆矩阵
，而 BFGS 算法中选择
逼近海赛矩阵
，相应的拟牛顿条件

假设每一步迭代中矩阵
是由
加上两个附加项构成，即

其中，
与
是待定矩阵。则

为使
满足拟牛顿条件，可使
与
满足

可取

可得矩阵
的迭代公式

可以证明，如果初始矩阵
是正定的，则迭代过程中的每个矩阵
都是正定的。

BFGS 算法：
输入：目标函数
，梯度
，精度要求

输出：
的极小点

1. 取初始点
   ，取
   为正定矩阵，置

2. 计算
   ，若
   则停止计算，得近似解
   ；否则，转 3.

3. 由
   求出

4. 一维搜索，求
   使
   

5. 置

6. 计算
   ，若
   ，则停止计算，近似解
   ；否则，计算
   

7. 置
   ，转 3.

6： Broyden 类算法 (Broyden’s algorithm)

我们可以从 BFGS 算法矩阵
的迭代公式得到 BFGS 算法关于
的迭代公式。

记

两次应用 Sherman-Morrison 公式，得

称为 BFGS 算法关于
的迭代公式。

其中 Sherman-Morrison 公式：假设
是
阶可逆矩阵，
是
维向量，且
也是可逆矩阵，则：

令由 DFP 算法
的迭代公式得到的
记作
，由 BFGS 算法
的迭代公式得到的
记作
，由于
和
均满足拟牛顿条件，则两者的线性组合

也满足拟牛顿条件，而且是正定的。其中，
。该类算法称为 Broyden 类算法。

7： 参考文献

李航：《统计学习方法》，清华大学出版社

Jacobian 矩阵和 Hessian 矩阵

梯度下降（Gradient Descent）小结

https://hackernoon.com/gradient-descent-aynk-7cbe95a778da

牛顿法与拟牛顿法学习笔记
https://zhuanlan.zhihu.com/p/37524275