六、非完全信息策略式博弈

前面的五节笔记讲的都是完全信息的策略式博弈，而这一章才开始一个新的类别——非完全信息策略式博弈。

一、引言：非完全信息

在一场博弈中，玩家可能并不知道其他玩家的收益、偏好等等。这些情况下的博弈，称为非完全信息的博弈(Incomplete Information)。在非完全信息策略式博弈中，我们考虑一种情况：玩家有一个隐藏的“状态”，在不同的状态下，收益矩阵不同。其他的非完全信息策略式博弈都可以转化为这种模型。

二、例：(非完全信息)

男生和女生决定去看足球(F)还是去看芭蕾(B)，如果两个人都知道对方喜欢自己，那么这是一个完全信息博弈，收益矩阵是这样的：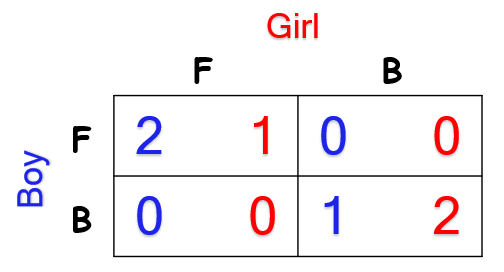

现在假设这样的情况：女生知道男生喜欢她，但是男生却不知道女生的意愿(女生自己是知道的)。不过，男生也并不是一点信息都没有，他知道女生喜欢他的概率为p。这样，收益矩阵就变成了：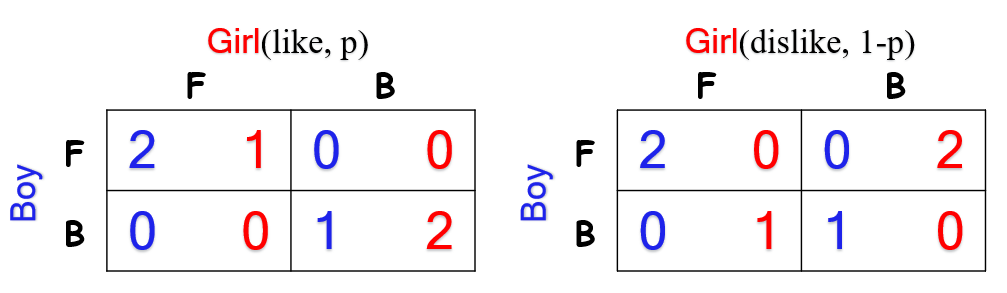

这样的话，如何计算纳什均衡呢？
如果Boy选择F，Girl在喜欢的状态下，F是最优反应，在不喜欢的状态下，B是最优反应。这个时候，如果F是Boy的最优反应，那么(F,(F,B))就构成纳什均衡了。
那么，F是不是B的最优反应？什么时候才是B的最优反应呢？这就要计算Boy选择F时候的期望收益。Boy如果选择F，有p的概率收益是2，有1-p的概率收益是0。因此，期望收益为：

在其他玩家策略不变的情况下，玩家收益最大的策略是最优反应。上面已经计算了Boy选择F的期望收益，现在要计算在女生策略不变的情况下，Boy选择策略B的收益：

因此，当也就是时，是纳什均衡。
同理，讨论Boy选B的情况，先计算女生的最优反应，再计算男生的最优反应，计算出p的范围是多少的时候，会有纳什均衡。结果是时，是纳什均衡。

三、形式化：贝叶斯博弈(Bayesian Games)

策略式博弈是贝叶斯博弈，其中：

• 是玩家集
• 是策略集
• 是状态集，表示每个人的私有的信息。给定状态，收益是确定的。
• 表示在上的联合分布。
• 玩家的纯策略，表示在玩家的所有状态下的策略选择。，(假设有种状态)
• 收益函数。表示在这些博弈结果和这些状态下的收益。

这里面，需要仔细说说，它表示每个人的隐藏的状态信息，每个玩家知道自己的状态，但是不知道其他人的状态。如果所有人都只有一个状态，那么就是完全信息的。一般来说，我们研究状态独立的情形，每个人的状态都是独立的，也就是。
根据贝叶斯规则，有

其中
博弈结果
给定，玩家的期望收益：

意思：在当前的状态下，对手的某种状态的概率，乘以这种状态下他们的策略选择的收益，求和。

四、贝叶斯纳什均衡

若博弈结果对于所有的和，满足：

则称这个博弈结果是纳什均衡。

最优反应函数

玩家的在给定和的最优反应为：

定理

博弈结果是纳什均衡当且仅当对于每个和，都有

五、例子：古诺模型(非完全信息)

上面性别战是离散的例子，这里举一个古诺模型。
有两家公司生产同一种商品，这种商品的成本可能有两种：高价和低价，公司1的成本是，这是众所周知的。然而公司1不知道公司2的成本是还是，它相信公司2成本是的概率是。市场上可以卖出的商品单价是(商品总产量)，现在两家公司需要决定各自的产量。
建模：

• 
• ，
• ，
• 单价：或

求解纳什均衡：
对于公司1，求它的期望收益(公司1以p的概率相信公司2是)：

对于公司2，如果它成本是，则期望收益为：

对于公司2，如果它成本是，则期望收益为：

用期望收益对产量求导等于零，得出收益的极大值点，也就是最优反应函数：



求得纳什均衡：

六、总结

这一节讲了非完全信息策略式博弈，主要是多了”私有状态”这一个概念。状态多的时候，纳什均衡很难求。