Q:什么是机器学习?
机器学习最初被定义为 “不显式编程地赋予计算机能力的研究领域”。很明显,这里的“机器” 是指计算机。通常我们给计算机编程都会使用 if-else 这些流程控制:
if(今天是周末){在家睡觉}else{好好工作}
这就是直接地、明显地(显式地)告诉了计算机什么时候应该做什么。
机器学习则不是直接告诉计算机什么时候做什么,而是提供一些案例(训练数据),让计算机通过案例自己学习,自己摸索什么时候应该做什么。一个著名的例子是给计算机输入一大堆 “房价 - 房屋面积” 数据,让计算机自己发现房价和房屋面积的规律,然后我们输入一个新的房屋面积数据,计算机就可以根据学习到的规律输出相应的房价。
机器学习的根本任务是预测。
“机器学习”同时也是一门学科,研究怎样使得计算机更好地学习,亦即,是一门研究 “学习算法” 的学科,主要任务是评估 “学习算法” 的好坏以及开发新的 “学习算法”。这里的“学习算法” 是计算机的学习方法,本质上是一种基于现有的数据产生预测模型的算法。
Q:学习一门学科需要先掌握其基本概念,“机器学习” 领域有哪些需要掌握的重要概念?
人类观察事物时,是通过观察事物的本质特征来认识事物的。比如观察西瓜,会观察西瓜的色泽、根蒂、敲声等特征。假设我们收集了一批关于西瓜的数据:
(色泽=青绿;根蒂=蜷缩;敲声=浊响)(色泽=墨绿;根蒂=稍蜷;敲声=沉闷)(色泽=浅白;根蒂=硬挺;敲声=清脆)······
假设我们希望用这一批数据来让计算机学习
1、样本、示例、记录——这批数据里的每对括号。
2、数据集——这组样本(示例、记录)的集合。
3、特征、属性——色泽、根蒂、敲声等反映一个事物的本质的可观察方面。
4、属性值——青旅、墨绿、蜷缩、浊响等,是属性的取值。
5、属性空间、样本空间、输入空间——属性张成的空间。这似乎是线性代数的语言,亦即把属性当作坐标轴,形成一个空间,那么样本就是这个空间中一个个的点。例如,吧 “色泽”、“根蒂”、“敲声” 作为坐标轴,则长生了一个三维空间,每个西瓜都是这个空间里的一个点。
6、维数——样本空间的坐标轴数,也就是数据集的特征数量。本例中的维数是 3。
7、假设——也称假设函数,指计算机通过学习后得到的一个函数(预测模型)。
8、标记——关于样本结果的信息,比如一个 (色泽 = 青绿;根蒂 = 蜷缩;敲声 = 浊响)的西瓜是好瓜,那么“好瓜” 就是(色泽 = 青绿;根蒂 = 蜷缩;敲声 = 浊响)这个样本的标记。
9、样例——带有标记的样本,比如((色泽 = 青绿;根蒂 = 蜷缩;敲声 = 浊响),好瓜)
10、标记空间、输出空间——所有标记的集合。本例中就是指{好瓜、坏瓜}。
11、泛化——如果用某个数据集的样本训练出的一个模型(假设函数),能够适用于新的样本数据,就说这个模型具有泛化能力。模型能适用于越多的新数据,则说明其泛化能力越强。
Q:《机器学习》为 “假设空间” 这个概念另起一节说明,那么什么是“假设空间”?
“假设空间”里的 “假设” 指的是假设函数,也就是机器学习的成果。例如我们做分类学习,那么通过数据训练后得到的分类模型就是我们得到的假设。
假设空间是指所有可能假设组成的空间。也可以说是所有在表达形式上符合任务要求的假设函数的集合。
对于西瓜分类任务,我们要获得的假设函数的形式是
假设 “色泽”、“根蒂”、“敲声”3 个特征都有 3 种可能取值,那就有 4_4_4+1=65 种可能假设,亦即假设空间的大小为 65。
对于根据房屋大小预测房价的问题,我们要后的的假设函数的形式则是
这个问题的假设空间是无穷大。
因此,学习过程可以看作在假设空间中寻找符合训练数据集的假设的过程。
Q:什么是 “归纳偏好”?
A:
在西瓜分类问题中,可能由于数据集的原因,我们会得到多个符合数据集的假设函数,比如:
好瓜→(色泽=墨绿)^(根蒂=蜷缩)^(敲声=沉闷)好瓜→(色泽=青绿)^(根蒂=*)^(敲声=沉闷)
这所有训练后得到的假设组成的空间称为 “版本空间”。
那么版本空间中哪一个假设 比较好?
如果我们认为越精细越好,则选择
好瓜→(色泽=墨绿)^(根蒂=蜷缩)^(敲声=沉闷)
如果我们认为越粗略越好,则选择
好瓜→(色泽=青绿)^(根蒂=*)^(敲声=沉闷)
像上面那样,计算机的学习算法基于某种偏好认为某个假设比其他假设好,那么我们说这个学习算法有 “归纳偏好”。事实上所有“学习算法” 都有归纳偏好,而且一般来说会偏好那些形式简单的假设。
Q:什么是 NFL 定理?其推导如何?
A:
NFL(No Free Lunch)定理,翻译过来就是 “没有免费午餐” 定理,收的是在机器学习中,没有给定具体问题的情况下,或者说面对的是所有问题的情况下,没有一种算法能说得上比另一种算法好。换成我们的俗话讲,就是 “不存在放之四海而皆准的方法”。只有在给定某一问题,比如说给“用特定的数据集给西瓜进行分类”,才能分析并指出某一算法比另一算法好。这就要求我们具体问题具体分析,而不能指望找到某个算法后,就一直指望着这个“万能” 的算法。这大概也是 no free lunch 名字的由来吧。
这个定理怎么得出的?西瓜书里有这样一段文字:

似乎说的是我?
好吧,仔细读一下推导过程,其实不难,连我这种数学渣渣都能读懂绝大部分。只要别被一长串推导吓到就行。
首先,定理推导的思路是证明对于某个算法 a,它在训练集以外的所有样本的误差,与 a 本身无关。
让我们一步一步来探索。
首先,误差是怎样表示,或者说怎样计算出来的?简单起见,只考虑二分类问题。那么误差就是分类器错判的个数与样本总数的比
其次我们要明确,一个算法,会产生很多不同的假设。更详细得说,一个算法的结果就是一个函数 h,但是 h 的参数不同,那么就会有 h1,h2 等不同的假设函数。最典型的是 h=kx+b。只要参数 k、b 不同,那么函数 h 就不同了。
那么,对于某个算法 a,它在训练集以外的所有样本的误差,就是它所能产生的所有假设 h,在训练集以外的所有样本上的误判率的和。
对于某个假设 h,“h 在某个数据集上的误差”与“在某个数据集中抽取一个能让 h 误判的样本的概率”是等价的问题。设 P(x)为 “在某个数据集中抽取一个能让 h 误判的样本的概率”,那就可以用 P(x) 来替代 h 的误差。
综上所述,对于某个算法 a,它在训练集以外的所有样本的误差就可以这样表示:

某个算法 a,它在训练集以外的所有样本的误差
对于二分类问题,设 f 为真正的分类函数,可能 f 有多个。假设其均匀分布,那么对于某个算法 a,它在训练集以外的所有样本的误差就可以表示成:
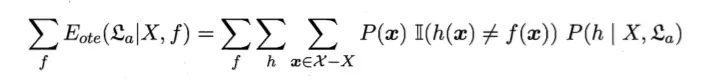
二分类问题中算法 a 在训练集外所有样本的误差
由乘法分配率可以化为
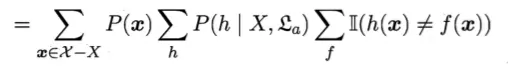
Paste_Image.png
又由于

Paste_Image.png
上式中最后意象可以被化简:
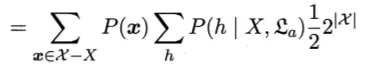
Paste_Image.png
又由全概率公式,或者说概率的可列可加性,下面这一项(上式中间那一项)其实等于 1
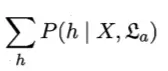
这一块其实等于 1,所有 h 的概率加起来嘛
如此一来,a 就在公式中消失了,于是最后的结果就是
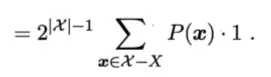
与 a 无关
所以说无论是什么算法,它在训练集以外所有样本上的误差都是上式表示的结果。
这就是 NFL 定理的推导。
本作品首发于简书 和 博客园平台,采用知识共享署名 4.0 国际许可协议进行许可。
https://www.jianshu.com/p/cbe8e0fe7b2c

