机器学习十大经典算法之最小二乘法_Wenrui Xie的博客-CSDN博客_最小二乘法

最小二乘法概述

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

简而言之，最小二乘法同梯度下降类似，都是一种求解无约束最优化问题的常用方法，并且也可以用于曲线拟合，来解决回归问题。

一元线性模型

如果以最简单的一元线性模型来解释最小二乘法。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面…

对于一元线性回归模型, 假设从总体中获取了 m 组观察值（X1，Y1），（X2，Y2）， …，（Xm，Ym）。对于平面中的这 m 个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

• （1）用 “残差和最小” 确定直线位置是一个途径。但可能会出现计算 “残差和” 存在相互抵消的问题。
• （2）用 “残差绝对值和最小” 确定直线位置也是一个途径。但绝对值的计算比较麻烦。
• （3）最小二乘法的原则是以 “残差平方和最小” 确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。

为了计算β0,β1 的值，我们采取如下规则：β0,β1 应该使计算出来的函数曲线与观察值的差的平方和最小。即 Cost 函数，用数学公式描述就是：

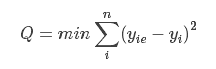
其中， y i e y_{ie} yie表示根据 y=β0+β1x 估算出来的值，yi 是观察得到的真实值。

明确了前面的 cost function 以后，后面的优化求解过程反倒变得 s 容易了。
样本的回归模型很容易得出：

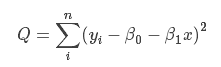
现在需要确定β0、β1，使 cost function 最小，即对公式进行求导，函数的极小值点为偏导为 0 的点。

将这两个方程稍微整理一下，使用克莱姆法则，很容易求解得出：

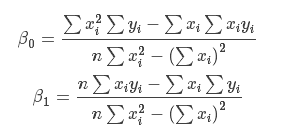
这就是最小二乘法的解法，就是求得平方损失函数的极值点。需要注意的一点是β0 是常数项对应的系数，此处相当于添加了一个特征值 x0 且 x0 恒为 1，也就是目标函数中的β0 可以看成β0x0, 这样的话就不同单独考虑常数项了 (在后面的多元线性模型就用到了该性质)。

多元线性模型

如果我们推广到更一般的情况，假如有更多的模型变量 x1,x2,⋯,xn，可以用线性函数表示如下：

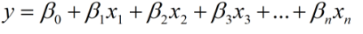
对于 m 个样本来说，可以用如下线性方程组表示：

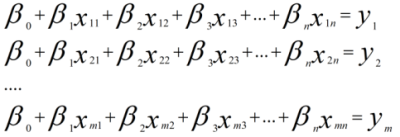
如果将样本矩阵 xij 记为矩阵 A, 将参数矩阵记为向量β，真实值记为向量 Y，上述线性方程组可以表示为：

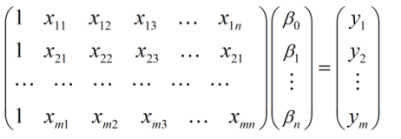
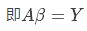
对于最小二乘来说，最终的矩阵表达形式可以表示为：

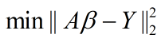
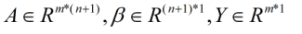
其中 m≥n, 由于考虑到了常数项，故属性值个数由 n 变为 n+1。

方程解法如下所示：

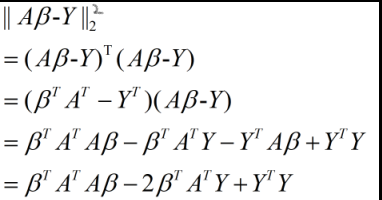
其中倒数第二行中的中间两项为标量，所以二者相等。然后利用该式对向量β求导：

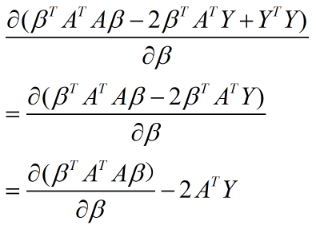
(1)

由矩阵的求导法则：
　

可知 (1) 式的结果为：

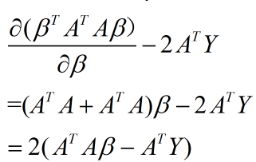
令上式结果等于 0 可得：

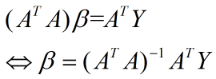
(2)

上式就是最小二乘法的解析解，它是一个全局最优解。

one more thing

1. 最小二乘法和梯度下降

(1) 最小二乘法和梯度下降法在线性回归问题中的目标函数是一样的 (或者说本质相同)，都是通过最小化均方误差来构建拟合曲线。

(2) 二者的不同点可见下图 (正规方程就是最小二乘法)：

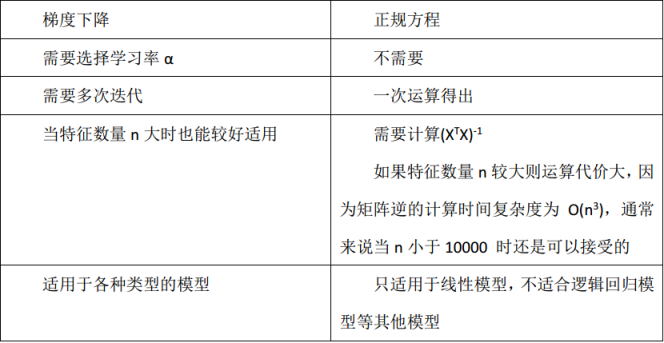
需要注意的一点是最小二乘法只适用于线性模型 (这里一般指线性回归)；而梯度下降适用性极强，一般而言，只要是凸函数，都可以通过梯度下降法得到全局最优值 (对于非凸函数，能够得到局部最优解)。

梯度下降法只要保证目标函数存在一阶连续偏导，就可以使用。

2. 最小二乘法的一些限制和解决方法：

要保证最小二乘法有解，就得保证ATA是一个可逆阵 (非奇异矩阵)；那如果 ATA 不可逆怎么办？什么情况下 ATA 不可逆？

关于 ATA 在什么情况下不可逆：

(1)当样本的数量小于参数向量 (即β) 的维度时，此时 ATA 一定是不可逆的。例如：你有 1000 个特征，但你的样本数目小于 1000 的话，那么构造出的 ATA 就是不可逆的。

(2) 在所有特征中若存在一个特征与另一个特征线性相关或一个特征与若干个特征线性相关时，此时 ATA 也是不可逆的。为什么呢？

具体来说假设, A 是 m*n 维的矩阵，若存在线性相关的特征，则 R(A)<n,R(AT)<n,R(ATA)<n, 所以 ATA 不可逆。

如果 ATA 不可逆，应该怎样解决？

(1) 筛选出线性无关的特征，不保留相同的特征，保证不存在线性相关的特征。

(2) 增加样本量。

(3) 采用正则化的方法。对于正则化的方法，常见的是 L1 正则项和 L2 正则项，L1 项有助于从很多特征中筛选出重要的特征，而使得不重要的特征为 0(所以 L1 正则项是个不错的特征选择方法)；如果采用 L2 正则项的话，实际上解析解就变成了如下的形式：

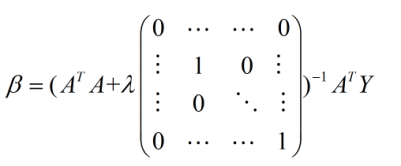
λ即正则参数 (是一种超参数) 后面的矩阵为 (n+1)*(n+1) 维，如果不考虑常数项的话，就是一个单位阵；此时括号中的矩阵一定是可逆的。

3. 最小二乘法的改进

最小二乘法由于是最小化均方差，所以它考虑了每个样本的贡献，也就是每个样本具有相同的权重；由于它采用距离作为度量，使得他对噪声比较敏感 (最小二乘法假设噪声服从高斯分布)，即使得他它对异常点比较敏感。因此，人们提出了加权最小二乘法，

相当于给每个样本设置了一个权重，以此来反应样本的重要程度或者对解的影响程度。

最小二乘法拟合多项式非线性函数

'''
最小二乘法拟合函数曲线f(x)
1、拟合多项式为：y = a0 + a1*x + a2*x^2 + ... + ak*x^k
2、求每个点到曲线的距离之和：Loss = ∑(yi - (a0 + a1*x + a2*x^2 + ... + ak*x^k))^2
3、最优化Loss函数，即求Loss对a0,a1,...ak的偏导数为0
    3.1、数学解法——求解线性方程组：
        整理最优化的偏导数矩阵为：X：含有xi的系数矩阵，A：含有ai的系数矩阵，Y：含有yi的系数矩阵
        求解：XA=Y中的A矩阵
    3.2、迭代解法——梯度下降法：
        计算每个系数矩阵A[k]的梯度，并迭代更新A[k]的梯度
        A[k] = A[k] - (learn_rate * gradient)
'''
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
'''
高斯列主消元算法
'''
# 得到增广矩阵
def get_augmented_matrix(matrix, b):
    row, col = np.shape(matrix)
    matrix = np.insert(matrix, col, values=b, axis=1)
    return matrix
# 取出增广矩阵的系数矩阵（第一列到倒数第二列）
def get_matrix(a_matrix):
    return a_matrix[:, :a_matrix.shape[1] - 1]
# 选列主元，在第k行后的矩阵里，找出最大值和其对应的行号和列号
def get_pos_j_max(matrix, k):
    max_v = np.max(matrix[k:, :])
    pos = np.argwhere(matrix == max_v)
    i, _ = pos[0]
    return i, max_v
# 矩阵的第k行后，行交换
def exchange_row(matrix, r1, r2, k):
    matrix[[r1, r2], k:] = matrix[[r2, r1], k:]
    return matrix
# 消元计算(初等变化)
def elimination(matrix, k):
    row, col = np.shape(matrix)
    for i in range(k + 1, row):
        m_ik = matrix[i][k] / matrix[k][k]
        matrix[i] = -m_ik * matrix[k] + matrix[i]
    return matrix
# 回代求解
def backToSolve(a_matrix):
    matrix = a_matrix[:, :a_matrix.shape[1] - 1]  # 得到系数矩阵
    b_matrix = a_matrix[:, -1]  # 得到值矩阵
    row, col = np.shape(matrix)
    x = [None] * col  # 待求解空间X
    # 先计算上三角矩阵对应的最后一个分量
    x[-1] = b_matrix[col - 1] / matrix[col - 1][col - 1]
    # 从倒数第二行开始回代x分量
    for _ in range(col - 1, 0, -1):
        i = _ - 1
        sij = 0
        xidx = len(x) - 1
        for j in range(col - 1, i, -1):
            sij += matrix[i][j] * x[xidx]
            xidx -= 1
        x[xidx] = (b_matrix[i] - sij) / matrix[i][i]
    return x
# 求解非齐次线性方程组：ax=b
def solve_NLQ(a, b):
    a_matrix = get_augmented_matrix(a, b)
    for k in range(len(a_matrix) - 1):
        # 选列主元
        max_i, max_v = get_pos_j_max(get_matrix(a_matrix), k=k)
        # 如果A[ik][k]=0，则矩阵奇异退出
        if a_matrix[max_i][k] == 0:
            print('矩阵A奇异')
            return None, []
        if max_i != k:
            a_matrix = exchange_row(a_matrix, k, max_i, k=k)
        # 消元计算
        a_matrix = elimination(a_matrix, k=k)
    # 回代求解
    X = backToSolve(a_matrix)
    return a_matrix, X
'''
最小二乘法多项式拟合曲线
'''
# 生成带有噪点的待拟合的数据集合
def init_fx_data():
    # 待拟合曲线f(x) = sin2x * [(x^2 - 1)^3 + 0.5]
    xs = np.arange(-1, 1, 0.01)  # 200个点
    ys = [((x ** 2 - 1) ** 3 + 0.5) * np.sin(x * 2) for x in xs]
    ys1 = []
    for i in range(len(ys)):
        z = np.random.randint(low=-10, high=10) / 100  # 加入噪点
        ys1.append(ys[i] + z)
    return xs, ys1
# 计算最小二乘法当前的误差
def last_square_current_loss(xs, ys, A):
    error = 0.0
    for i in range(len(xs)):
        y1 = 0.0
        for k in range(len(A)):
            y1 += A[k] * xs[i] ** k
        error += (ys[i] - y1) ** 2
    return error
# 迭代解法：最小二乘法+梯度下降法
def last_square_fit_curve_Gradient(xs, ys, order, iternum=1000, learn_rate=0.001):
    A = [0.0] * (order + 1)
    for r in range(iternum + 1):
        for k in range(len(A)):
            gradient = 0.0
            for i in range(len(xs)):
                y1 = 0.0
                for j in range(len(A)):
                    y1 += A[j] * xs[i]**j
                gradient += -2 * (ys[i] - y1) * xs[i]**k  # 计算A[k]的梯度
            A[k] = A[k] - (learn_rate * gradient)  # 更新A[k]的梯度
        # 检查误差变化
        if r % 100 == 0:
            error = last_square_current_loss(xs=xs, ys=ys, A=A)
            print('最小二乘法+梯度下降法：第{}次迭代，误差下降为：{}'.format(r, error))
    return A
# 数学解法：最小二乘法+求解线性方程组
def last_square_fit_curve_Gauss(xs, ys, order):
    X, Y = [], []
    # 求解偏导数矩阵里，含有xi的系数矩阵X
    for i in range(0, order + 1):
        X_line = []
        for j in range(0, order + 1):
            sum_xi = 0.0
            for xi in xs:
                sum_xi += xi ** (j + i)
            X_line.append(sum_xi)
        X.append(X_line)
    # 求解偏导数矩阵里，含有yi的系数矩阵Y
    for i in range(0, order + 1):
        Y_line = 0.0
        for j in range(0, order + 1):
            sum_xi_yi = 0.0
            for k in range(len(xs)):
                sum_xi_yi += (xs[k] ** i * ys[k])
            Y_line = sum_xi_yi
        Y.append(Y_line)
    a_matrix, A = solve_NLQ(np.array(X), Y)  # 高斯消元：求解XA=Y的A
    # A = np.linalg.solve(np.array(X), np.array(Y))  # numpy API 求解XA=Y的A
    error = last_square_current_loss(xs=xs, ys=ys, A=A)
    print('最小二乘法+求解线性方程组，误差下降为：{}'.format(error))
    return A
# 可视化多项式曲线拟合结果
def draw_fit_curve(xs, ys, A, order):
    fig = plt.figure()
    ax = fig.add_subplot(111)
    fit_xs, fit_ys = np.arange(min(xs) * 0.8, max(xs) * 0.8, 0.01), []
    for i in range(0, len(fit_xs)):
        y = 0.0
        for k in range(0, order + 1):
            y += (A[k] * fit_xs[i] ** k)
        fit_ys.append(y)
    ax.plot(fit_xs, fit_ys, color='g', linestyle='-', marker='', label='多项式拟合曲线')
    ax.plot(xs, ys, color='m', linestyle='', marker='.', label='曲线真实数据')
    plt.title(s='最小二乘法拟合多项式N={}的函数曲线f(x)'.format(order))
    plt.legend()
    plt.show()
if __name__ == '__main__':
    order = 10  # 拟合的多项式项数
    xs, ys = init_fx_data()  # 曲线数据
    # 数学解法：最小二乘法+求解线性方程组
    A = last_square_fit_curve_Gauss(xs=xs, ys=ys, order=order)
    # 迭代解法：最小二乘法+梯度下降
    # A = last_square_fit_curve_Gradient(xs=xs, ys=ys, order=order, iternum=10000, learn_rate=0.001)
    draw_fit_curve(xs=xs, ys=ys, A=A, order=order)  # 可视化多项式曲线拟合结果

参考文献链接

《矩阵分析与应用》

https://www.cnblogs.com/wangkundentisy/p/7505487.html

https://github.com/privateEye-zzy/Nonlinear_function_fitting/blob/master/Last_square_method_fit_curve.py
https://blog.csdn.net/xiewenrui1996/article/details/107418803