机器学习：用梯度下降法实现线性回归

之前在 机器学习算法数学基础之 —— 线性代数篇 里，总结过求解线性回归的两种方法：

1. 最小二乘法
2. 梯度下降法

这篇文章重点总结一下梯度下降法中的一些细节和需要注意的地方。

梯度下降法是什么

假设有一个估计函数：
，
其代价函数（cost function）为：

这个代价函数是 x(i) 的估计值与真实值 y(i) 的差的平方和，前面乘上 1/2，是因为在求导的时候，这个系数就不见了。

梯度下降法的流程：

1）首先对 θ 赋值，这个值可以是随机的，也可以让 θ 是一个全零的向量。
2）改变 θ 的值，使得 J(θ) 的值按梯度下降的方向减小。

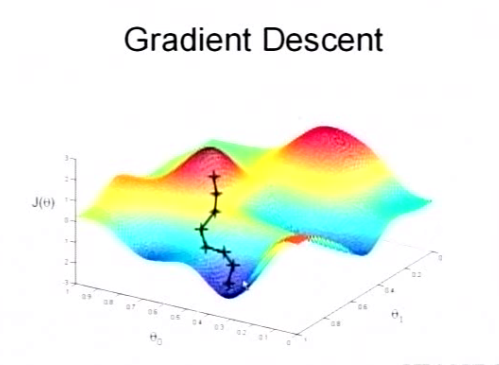
参数 θ 与误差函数 J(θ) 的关系图

红色部分表示 J(θ) 有着比较高的取值，我们希望能够让 J(θ) 的值尽可能的低，也就是取到深蓝色的部分。θ0、θ1 表示 θ 向量的两个维度。上面提到梯度下降法的第一步，是给 θ 一个初值，假设随机的初值位于图上红色部分的十字点。然后我们将 θ 按梯度下降的方向进行调整，就会使 J(θ) 往更低的方向进行变化，如图所示，算法的结束将在 θ 下降到无法继续下降为止。

θ 的更新：

θi 表示更新前的值，减号后边的部分表示按梯度方向减少的量，α 表示步长，也就是每次按梯度减少的方向变化多少。

梯度是有方向的，对于一个向量 θ，每一维分量 θi 都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化，就可以达到一个最小点，不管它是局部的还是全局的。

所以梯度下降法的原理简单来说就是：

在变量空间的某个点，函数沿梯度方向的变化率最大，所以在优化目标函数的时候，沿着负梯度方向减小函数值，可以最快达到优化目标。

特征缩放（Feature Scaling）

在 Stanford 的 Machine Learning 课程中，老师提到了使用梯度下降法时可能用到的特征缩放法，为的是当所要研究的数据集中出现数据值范围相差较大的 feature 时，保证所有 feature 有相近范围内的值。

以课程中的房价问题为例，数据集的 feature 中有房屋尺寸
和房间数量
两项，房屋尺寸的范围是 0~2000 feet^2，房间数量的范围是 1~5。此时以两个参数
和
为横纵坐标，绘制代价函数
的等高线图如下：

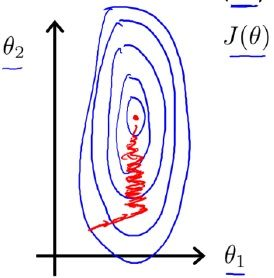
代价函数的等高线图

解决方法是对两个 feature 进行归一化处理：

x1 = size / 2000
x2 = number of rooms / 5

进行特征缩放后，代价函数的等高线图就变成了这样：

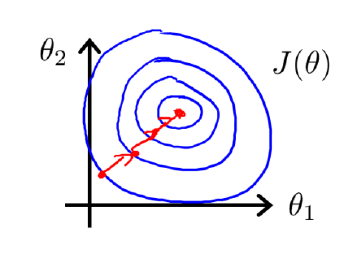
特征缩放后的代价函数等高线图

很明显，归一化处理前，代价函数的等高线图高又窄，在梯度下降过程中，需要反复迭代很多次，才能达到理想的位置，会花费较长的时间。归一化处理后，两个 feature 的数值大小处于相近的范围内，因此横纵坐标
和
两个参数的变化范围也变得相近，对
的影响不再有 feature 值在范围大小伤的影响，从而反映代价函数上。在等高线图上，梯度下降过程中变化受 x1 大小影响的
的变化减小了，变得和 x2 的变化趋势一致，从而等高线图近似圆形。

至于把 feature 缩小到什么范围，没有特别的要求，只要各个 feature 的数值范围相近就可以了，只是为了计算速度可以有所提升。

顺便引用一下 Andrew Ng 老师在课程中用到的例题：

步长 α（学习率）的选择

在参数
的更新式：
中，
称为步长，决定了参数每次被增加或减小的大小，步长如何选择是决定梯度下降法表现的一个因素。如果步长过大，可能会直接越过最佳点，导致无法收敛，甚至发散；如果步长过小，可能导致迭代次数过多，降低效率。

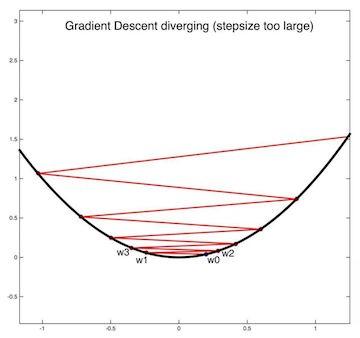
步长的选择过大时，导致越过最佳点

关于步长的选择，有很多种方法，如果初始步长不合适，在后边要不断进行调整，调整的方法有很多种，关于这个问题国内外也有很多论文对其研究过。一旦找到了合适的步长，大多数情况下就不需要再改变了，有人会觉得随着
越来越小，如果步长不变，更新式中第二项的值也会越来越小，迭代的进度会慢下来。但是，随着越来越接近最佳点，梯度也会越来越大，也就是
的微分值也会越来越大，所以迭代的速度并不会变慢。

最常用的选择步长的方法是按 3 倍调整，即：0.001、0.003、0.01、0.03、0.1、0.3、1 …… 按这个倍率进行测试，寻找能使
下降速度最快的步长范围，确定范围后再对其进行微调。

用 Python 实现梯度下降法

import numpy as np import random def gradient_descent(alpha, x, y, ep=0.0001, max_iter=10000): converged = False iter = 0 m = x.shape[0] # 数据的行数 # 初始化参数(theta) t0 = np.random.random(x.shape[1]) t1 = np.random.random(x.shape[1]) # 代价函数, J(theta) J = sum([(t0 + t1*x[i] - y[i])**2 for i in range(m)]) # 进行迭代 while not converged: # 计算训练集中每一行数据的梯度 (d/d_theta j(theta)) grad0 = 1.0/m * sum([(t0 + t1*x[i] - y[i]) for i in range(m)]) grad1 = 1.0/m * sum([(t0 + t1*x[i] - y[i])*x[i] for i in range(m)]) # 更新参数 theta # 此处注意，参数要同时进行更新，所以要建立临时变量来传值 temp0 = t0 - alpha * grad0 temp1 = t1 - alpha * grad1 t0 = temp0 t1 = temp1 # 均方误差 (MSE) e = sum( [ (t0 + t1*x[i] - y[i])**2 for i in range(m)] ) if abs(J-e) <= ep: print 'Converged, iterations: ', iter, '!!!' converged = True J = e # 更新误差值 iter += 1 # 更新迭代次数 if iter == max_iter: print 'Max interactions exceeded!' converged = True return t0,t1

参考：3 Types of Gradient Descent Algorithms for Small & Large Data Sets

相关文章：

第一时间了解更多大数据相关内容，欢迎关注微信公众号【数据池塘】：
https://zhuanlan.zhihu.com/p/33992985