序言中介绍了博弈的要素和博弈的分类，那么，怎么“论”呢？当下最重要的，是将博弈用数学语言来描述出来，也就是形式化。
博弈不同的分类：{策略式，扩展式}，{完全信息，非完全信息}等等，都有不同的形式化表示，这一节介绍最简单的一种：完全信息策略式博弈。
与之对应的例子有：囚徒困境(Prisoners’ Dilemma)、古诺竞争(Cournot Competition)。
对了，顺便提一下，博弈不是“搏”而是“博”，哈哈，一开始学的时候写错了。
一、一些概念的定义
1. 策略式博弈
策略式博弈也叫静态博弈，它是一次博弈：
- 所有玩家同时做策略选择
- 知道对手可选的策略
- 不知道对手具体会选哪一个策略
- 非合作
典型的例子是：石头剪刀布。
与策略式博弈相对应的是扩展式博弈(动态博弈)。
2. 完全信息
所有玩家都知道在一组策略选择下的每个人的收益。
下面把完全信息策略式博弈简写为：策略式博弈
二、策略式博弈形式化
形式化主要是将博弈的要素用数学语言表示出来。对于一个策略式博弈，用{玩家、策略、收益}就可以完全表示。
1. 基础概念的定义
一个策略式博弈包括：
- 玩家集N：玩家的有限集合
- 每个玩家
都有策略集
，表示他可以选择的策略的集合 - 每个玩家
都有收益函数
：
，表示在一组策略下它的收益
此外，有如下定义：
- 博弈结果：
，是一组策略构成的元组 - 博弈结果空间：
，则
- 对手策略：
，则
在策略式博弈中，收益的具体数值并不重要，重要的是收益之间的大小关系，称作偏好关系。任何满足全序关系的集合，都可以用来表示收益。我们通常用实数来表示收益。
2. 形式化
就是前面定义的那样。
3. 例子：囚徒困境形式化
- 玩家集：
，表示1、2两个囚徒 - 策略集：
，为了书写简便，用c表示坦白，用d表示沉默 - 收益函数：
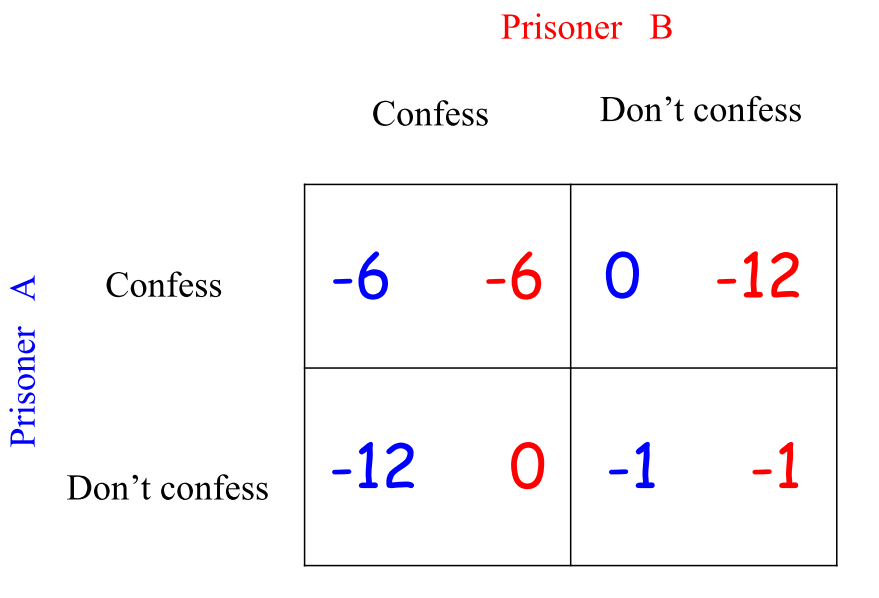
- 用收益矩阵表示如下：
三、纳什均衡
我们自然地会去想，在这种条件下，两个囚犯会选择怎样的策略呢？先从A的视角想一下，
- 如果B坦白：A选择坦白，收益是(-6)；A选择沉默，收益是(-12)，因此A会坦白。
- 如果B沉默：A选择坦白，收益是(0)；A选择沉默，收益是(-1)，因此A会坦白。
1. 纳什均衡的想法
从上面的思考中，可以看出这种思想：当对手策略选定的时候，我会调整自己的策略，使得自己收益在几种策略选择中是最大的，这时的策略称为“最优反应”。这个时候，如果对手不改变策略的话，我是没有动机去改变自己的策略的。
如果每个人的策略都是“最优反应”，那么就会形成一种稳定的局面，这时的博弈结果就是纳什均衡
2. 纳什均衡形式化定义
纳什均衡(Nash equilibrium)是博弈结果
，使得对于每个玩家
都有：
(对手策略选定的时候，自己最优)纳什均衡简写为：NE
3. 纳什均衡求解：寻找最优反应
玩家
关于对手策略
的最优反应：
同时满足所有人的最优反应的博弈结果，就是纳什均衡。也就是满足
的博弈结果。
4. 例1：依旧是囚徒困境
在收益矩阵上标出这些最优反应：
表示在囚徒2选择c的时候，囚徒1会选择c，因为囚徒1的收益(-6 > -12)。对应矩阵中左边红色的”√“。
详细分析如下：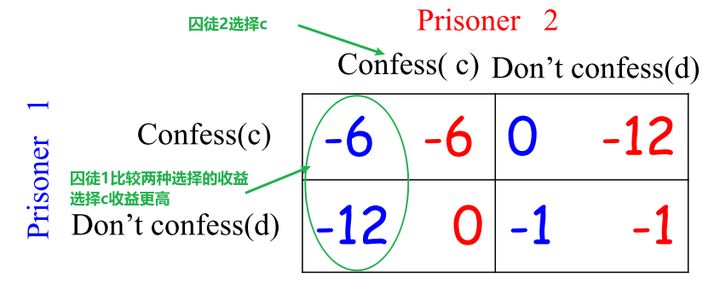
表示在囚徒2选择d的时候，囚徒1会选择c，因为囚徒1的收益(0 > -1)。对应矩阵中右边红色的√。
表示在囚徒1选择c的时候，囚徒2会选择c，因为囚徒2的收益(-6 > -12)。对应矩阵中上边绿色的√。
表示在囚徒1选择d的时候，囚徒2会选择c，因为囚徒2的收益(0 > -1)。对应矩阵中下边绿色的√。
因此，最终得到满足所有人最优反应的结果：(c,c)，也就是两人都坦白。
5. 例2：古诺竞争
这个例子收益是连续的，不能用矩阵来表示。问题如下：
两个厂商{1, 2}生产和销售同一种商品，厂商
生产的数量记为
。 每件商品生产成本都是c，售价是：
求纳什均衡
1) 形式化
。(售价-成本)x生产数量
2) 求最优反应函数
对于厂商1：
- 如果
，那么对于任意的
，都有
，即没有正收益 - 如果
，那么
。 - 固定
，
何时取最大呢？求导！ - 求解：
， - 求得
，这就是厂商1的最优反应函数
3) 纳什均衡
对于满足纳什均衡的博弈结果
，有：
联立方程，解得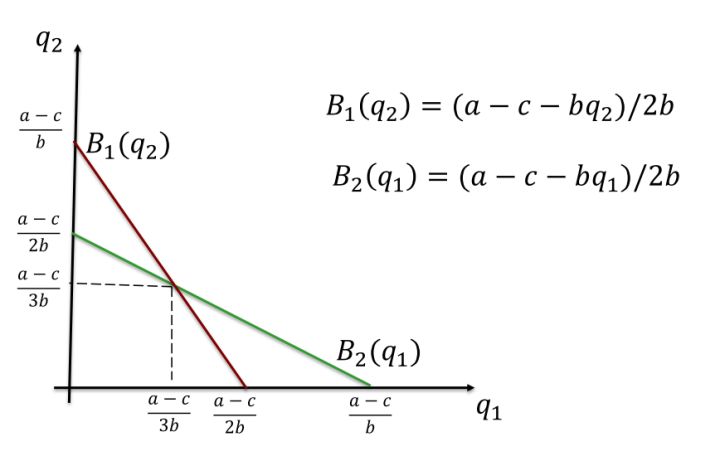
最优反应相交之处
四、小结
这节学习了：
- 策略式博弈形式化
- 纳什均衡的定义及求解
重要的是理解纳什均衡所表示的意义。纳什均衡并不一定是最优的结果，它是一种稳定的局面，在这种情况下，所有人都没有动机去改变自己的选择。
若有收获，就点个赞吧
0 人点赞
