自动编码器(AutoEncoder):是SAE的基本组成的单元,结构如图
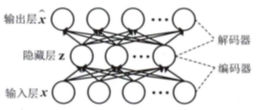
AE由输入层、隐藏层与输出层组成, 其中输入层用于接收样本输入,隐藏层提取数据特征,输出层用于重构输入数据。输入层与隐藏层神经元数量可以不同,但与输出层的神经元数量相同。输入层与隐藏层组成编码器(encoder),隐藏层与输出层组成解码器(decoder)。AE提取数据特征的方法是对样本进行重构,这个过程可分解为编码与解码两个步骤, 分别由编码器与解码器来完成。
如图4.8本文使用的是一个两个隐含层的网络结构,在构建该网络时,通过两个自动编码器(AE)来进行叠加,每一个AE 在训练时都是逐层训练的,通过最小化原始输入与重构输出之间的误差,进行训练,然后将该层的输出作为下一个AE 的输入。按照这个方法依次训练各个层,最后得到一个SAE 的学习模型,将SAE 的输出层去掉,将特征输入到逻辑回归层Softmax 中,将下一时刻的交通量的值作为标签.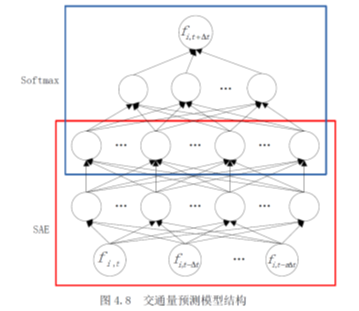
该交通量的预测模型的输入为几个相邻路段的当前时刻及几个历史时刻的交通量,交通量的值为整数且在一定的取值范围内,因此可以直接当作类别标签作为输出,预测输入所属于的类别值即可以当作是预测下一时刻的某路段的交通量的值。
该模型的训练过程可以概括如下五个步骤:
(1) 将训练集作为自动编码器的输入,通过最小化目标函数来训练第一层,将第一层作为一个自动编码器。
(2) 将第二层作为一个自动编码器,将第一层的输出作为该自动编码器的输入。
(3) 如(2)中迭代所需的层数。
(4) 使用最后一层的输出作为预测层的输入,并且随机地或通过监督训练来初始化其参数。
(5) 以监督的方式用BP 方法微调所有层的参数。
SAE 的学习功能实现的是对交通量数据样本的深层特征的挖掘,并不对新样本进行预测。因此需要将该学习模型的输出特征作为预测层的输入,本文利用逻辑回归来进行交通量的预测。通过输入特征向量的确定,以及模型的训练过程,本文确定了基于SAE的交通量预测模型。
参数:
l 输入向量X:
对于这个模型,首先需要定义与交通量相关的输入特征向量。由于交通量的时空特性可以发现,相邻的链路之间的交通量是相互关联相互影响的。因此,本文中定义该模型的输入特征向量 如公式所示。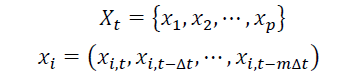
其中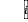 =1,2,…,
=1,2,…,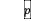 ,
,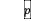 表示
表示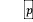 个路段,
个路段,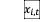 表示第
表示第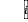 个路段在
个路段在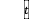 时刻的交通量, 任意
时刻的交通量, 任意
一个路段的下一时刻的交通量是由相邻几个路段的当前时刻以及前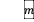 个时刻的交通量数据来进行预测的。
个时刻的交通量数据来进行预测的。
l 隐含层的数目(注:matlab程序中也是两层)
从这个表中可以看出,对于单隐层来说,增加隐含层的数目,有利于提高一定的预测精度,从结果上来看,当隐含层数目为2 时,本模型的预测效果比其他隐含层数目的结果稍好一些。因此,可以确定该模型的隐含层数目为两层。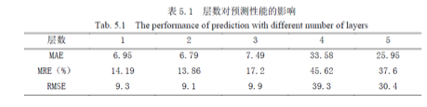
注:本文中基于交通量和交通平均速度的预测模型中,对于预测模型的性能分析主要是对于回归任务的性能度量,比较常见的几种性能指标有均方误差(MSE),平均绝对误差(MAE),平方根误差(RMSE)。
l 隐含层节点的数目(注:MATLAB程序中用的数目是200)
为了便于研究,这里本文使得所有的隐含层的节点数目相同。由于已经确定了隐含层的数目,因此,本文分别取隐含层节点数为{100,200,300,400,500,600},对模型的性能进行分析。如表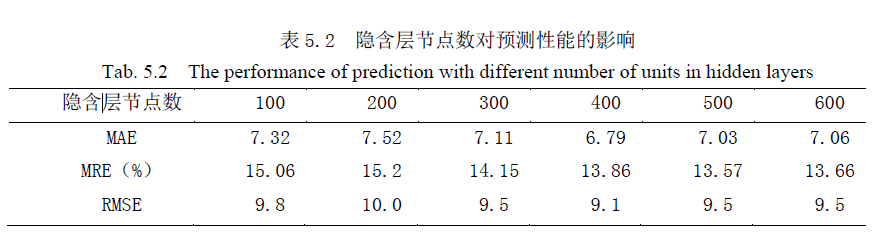
从表5.2 中可以看出,当隐含层节点数不同时,该模型的预测性能也不同。当隐含层的节点数目为400 时,模型的预测效果最好,因此本文使每个隐含层的节点数目分别为400。这样,本文已经确定了整个交通量预测模型中SAE 的层数及隐含层的节点数。
l 输入特征向量的维度:(4维)
该模型的输入向量,取的是当前时段的和前几个历史时段的几个相邻路段的
交通量,并且已经确定了路段的数目,因此,本文需要确定历史时段的取值个数,以此来确定输入特征向量的维度。在本文中,该模型分别取1 至12 的整数来表示历史时段的取值个数。
经过验证确定,当历史时段的取值为4 的时候,本文的交通量预测模型表现最好。即,分别取了三个路段上的当前时段的交通量以及前4 个时间的交通量,来预测下一个时段的交通量。
l 训练学习效率 :(动态变化的—递减)
:(动态变化的—递减)
Ø Introduction
学习率 (learning rate),控制模型的 学习进度 :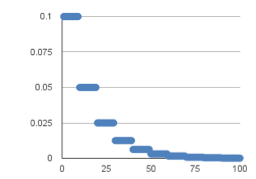
Ø 学习率大小
| 学习率 大 | 学习率 小 | |
|---|---|---|
| 学习速度 | 快 | 慢 |
| 使用时间点 | 刚开始训练时 | 一定轮数过后 |
| 副作用 | 1.易损失值爆炸;2.易振荡。 | 1.易过拟合;2.收敛速度慢。 |
Ø 学习率设置
在训练过程中,一般根据训练轮数设置动态变化的学习率。
刚开始训练时:学习率以 0.01 ~ 0.001 为宜。
一定轮数过后:逐渐减缓。
接近训练结束:学习速率的衰减应该在**100倍以上**。
Note: 如果是 迁移学习 ,由于模型已在原始数据上收敛,此时应设置较小学习率 () 在新数据上进行 微调 。
l 学习率减缓机制
| 轮数减缓 | 指数减缓 | 分数减缓 | |
|---|---|---|---|
| 英文名 | step decay | exponential decay | decay |
| 方法 | 每N轮学习率减半 | 学习率按训练轮数增长指数插值递减 | 控制减缓幅度, 为训练轮数 |
l 把脉目标函数损失值 曲线
理想情况下 曲线 应该是 滑梯式下降 [绿线]: 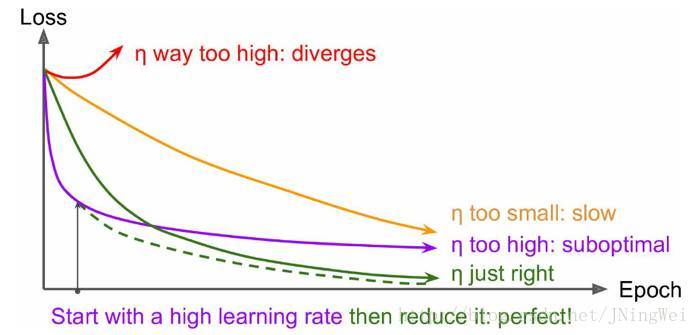
1、 曲线 初始时 上扬 [红线]
Solution:初始 学习率过大 导致 振荡,应减小学习率,并 从头 开始训练 。
2、 曲线 初始时 强势下降 没多久 归于水平 [紫线]:
Solution:后期 学习率过大导致无法拟合,应减小学习率,并重新训练后几轮 。
3、 曲线 全程缓慢 [黄线]:
Solution:初始学习率过小导致 收敛慢,应增大学习率,并从头开始训练 。
l 每个训练周期:
与计算性能和学习率有关
l 算法时间复杂度:
需要根据学习率计算和算法来计算
l 训练数据集(matalab中把数据分了10类)

