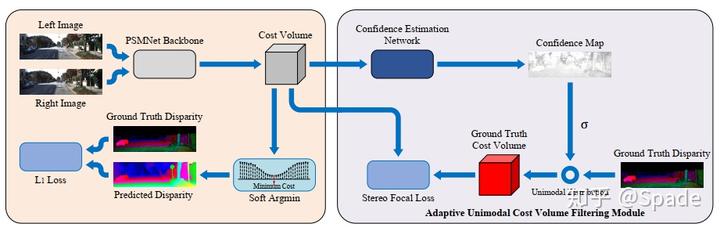
Adaptive Unimodal Cost Volume Filtering for Deep Stereo Matching,用于代价体的自适应单峰滤波,被 AAAI2020 接收。本文主要工作在于:在当前串联特征得到 cost volume,再 3D 卷积这一套的基础上,考虑增加对最终代价聚合结果的约束。
左右图经过共享权重的网络得到 C×H×W 的特征图,根据不同视差寻找到对应的右图特征,二者串联,可以得到 2C×D×H×W 的 cost volume,用 3D 卷积进行代价聚合,最终得到 D×H×W 的代价聚合结果(这里是匹配代价还是负的匹配代价是一样的,对于网络的学习,无非就是卷积核全取相反数)。取 softmax 转化为概率,用下式计算得到视差结果。
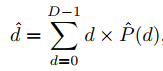
从这个式子可以看出,不同的概率分布,是有可能通过加权计算得到相同的视差结果的。也就是说,不同的代价分布都可能计算得到准确的视差值,但这些分布中,大部分都是不合理的。因此,本文对这个分布进行约束,使网络学习最合理的代价分布。
显然,最正确的分布应该是在视差真值处匹配代价最小,距离真值越远,匹配代价越大。据此,我们可以用真值构造一个高斯分布,迫使网络学习得到最合理的概率分布。那么高斯分布的均值就是视差真值了,接下来就是如何确定方差。
我们知道,纹理较少的区域通常匹配代价会比较模糊,因为相邻的像素特征可能非常接近,因此,在这些点,匹配代价的分布应该是较平缓的。从另一个角度讲,这些点的误差是有可能比较大的,也就是置信度比较低的,因此,我们可以用一个置信度描述分布的标准差,置信度越低,分布越平缓,标准差越大。在本文中,置信度是网络输出的结果,而最终的结果也表明,置信度低的区域就是这些纹理弱的区域和难以匹配的遮挡区域。
这里 cost volume 指的是经过 3D 卷积的代价聚合后的结果,是 D×H×W 的。网络得到分布与真值构造的分布计算差异的方式是加权的交叉熵损失(会对占比更小的正样本分配更大的权重):
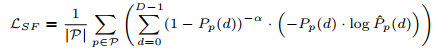
除此外,还有一项正则化损失,希望网络输出尽可能多高置信度的点:
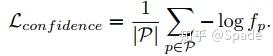
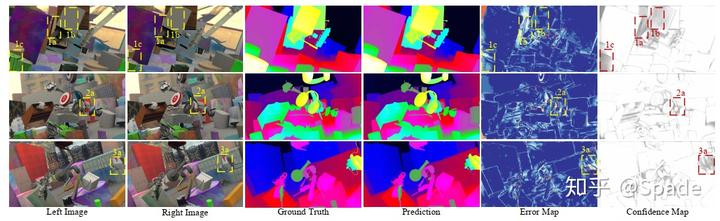
从实验结果中看,置信度和误差图很好地对应了起来:
此外,之前谈到本文对概率分布施加约束,相当于从众多解中寻找最合理的那个。因此,本文的方法也有较好的泛化性。
https://zhuanlan.zhihu.com/p/93641149

