关联规则算法

1.Apriori算法简介

Apriori算法是经典的挖掘频繁项集和关联规则的数据挖掘算法。A priori在拉丁语中指”来自以前”。当定义问题时，通常会使用先验知识或者假设，这被称作”一个先验”（a priori）。Apriori算法的名字正是基于这样的事实：算法使用频繁项集性质的先验性质，即频繁项集的所有非空子集也一定是频繁的。Apriori算法使用一种称为逐层搜索的迭代方法，其中k项集用于探索(k+1)项集。首先，通过扫描数据库，累计每个项的计数，并收集满足最小支持度的项，找出频繁1项集的集合。该集合记为L1。然后，使用L1找出频繁2项集的集合L2，使用L2找出L3，如此下去，直到不能再找到频繁k项集。每找出一个Lk需要一次数据库的完整扫描。Apriori算法使用频繁项集的先验性质来压缩搜索空间。

2. 基本概念

（1）项（Item）：是关联规则最基础的元素，用in（n=1,2,3…..）表示某一项。
（2）项集：是项的集合，假设项集I={i1，i2。。。。in}，包括n项的项集成为n项集。
（3）事务（TID）：是由一个唯一的事务标识号和一个组成事务的项的列表构成的。
（4）事务集：是所有事务构成的集合。假设事务数据集T={t1，t2。。。。tn}，
（5）关联规则：可以表示为行如所示的蕴涵式。其中，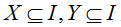
且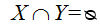
该关系式表示如果项集X在某一事物中出现时，那么项集Y也可能以某一概率出现在该事务中。
（6）支持度：是某一项集的频繁程度，是关联规则重要性的衡量准则，用于表示该项集的重要性。假设包含项集X、Y的事务数量与事务集总数countAll的比值,反映了X、Y项集同时出现的频率。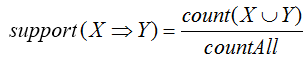

（7）置信度：用来确定Y在包含X的事务中出现的频繁程度，即Y在X条件下的条件概率，是对关联规则准确度的衡量准则，表示规则的可靠程度。假设包含项集X、Y的事务数量与项集X事务数量的比值：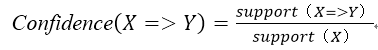

（8）频繁项集与最小支持度：最小支持度是预先设置好的项集满足支持度的下限，用Min_sup表示，反映了所关注的项集的最低重要性。当项集X的支持度不小于最小支持度阈值时，X为频繁项集：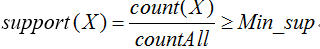

频繁项集中有两个重要的特性：

1. 如果一个项集是频繁的,那么它的所有非空子集都是频繁的。
2. 如果一个项集不是频繁的,那么它的所有超集也必然不是频繁的。

（9）强关联规则与最小置信度：最小置信度是预先设置好的项集满足置信度的下限 ，用Min_conf表示，反映了所关注的项集的最低可靠程度。当关联规则R同时满足支持度与置信度不小于最小阈值，则称其为强关联规则：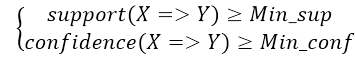

挖掘关联规则的主要任务就是为了找出满足条件的各种强关联规则。

3. Apriori算法实现

3.1挖掘频繁项集

3.1.1 相关定义

• 连接步骤：频繁(k-1)项集Lk-1的自身连接产生候选k项集Ck

  Apriori算法假定项集中的项按照字典序排序。如果Lk-1中某两个的元素（项集）itemset1和itemset2的前(k-2)个项是相同的，则称itemset1和itemset2是可连接的。所以itemset1与itemset2连接产生的结果项集是{itemset1[1], itemset1[2], …, itemset1[k-1], itemset2[k-1]}。连接步骤包含在下文代码中的create_Ck函数中。

• 剪枝策略
  

由于存在先验性质：任何非频繁的(k-1)项集都不是频繁k项集的子集。因此，如果一个候选k项集Ck的(k-1)项子集不在Lk-1中，则该候选也不可能是频繁的，从而可以从Ck中删除，获得压缩后的Ck。下文代码中的is_apriori函数用于判断是否满足先验性质，create_Ck函数中包含剪枝步骤，即若不满足先验性质，剪枝。

• 删除策略
  

基于压缩后的Ck，扫描所有事务，对Ck中的每个项进行计数，然后删除不满足最小支持度的项，从而获得频繁k项集。删除策略包含在下文代码中的generate_Lk_by_Ck函数中。

3.1.2 步骤

1. 每个项都是候选1项集的集合C1的成员。算法扫描所有的事务，获得每个项，生成C1（见下文代码中的create_C1函数）。然后对每个项进行计数。然后根据最小支持度从C1中删除不满足的项，从而获得频繁1项集L1。
   
2. 对L1的自身连接生成的集合执行剪枝策略产生候选2项集的集合C2，然后，扫描所有事务，对C2中每个项进行计数。同样的，根据最小支持度从C2中删除不满足的项，从而获得频繁2项集L2。
   
3. 对L2的自身连接生成的集合执行剪枝策略产生候选3项集的集合C3，然后，扫描所有事务，对C3每个项进行计数。同样的，根据最小支持度从C3中删除不满足的项，从而获得频繁3项集L3。
   
4. 以此类推，对Lk-1的自身连接生成的集合执行剪枝策略产生候选k项集Ck，然后，扫描所有事务，对Ck中的每个项进行计数。然后根据最小支持度从Ck中删除不满足的项，从而获得频繁k项集。
   

   3.2 由频繁项集产生关联规则

   一旦找出了频繁项集，就可以直接由它们产生强关联规则。产生步骤如下：

• 对于每个频繁项集itemset，产生itemset的所有非空子集（这些非空子集一定是频繁项集）；
  
• 对于itemset的每个非空子集s,如果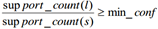，则输出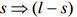，其中min_conf是最小置信度阈值。

  3.3 实例

  Apriori算法采用的是逐层搜索的迭代方法，其基本思想是利用遍历的方法计算频率，一层层进行查找，在生成的候选项集中找出哪些是频繁项集，用k项集探索( k + 1)项集。
  具体步骤：
  第一步：寻找频繁项集
  寻找频繁项集，逐层迭代搜索：通过扫描数据库，累计每个项的计数，并收集满足最小支持度的项，找出频繁1项集的集合，记为L1。然后，使用L1找出频繁2项集的集合L2，按照该方式不断迭代下去，直到不能再找到频繁k项集。
  第二步：产生强关联规则
  产生强关联规则，根据寻找到的Lk，利用非空子集构造规则，并找出满足条件的表达式，即强关联规则。
  实例：

对该算法中的各个步骤进行解释分析，假定事物数据库为Database D，最小支持度为50%：

　我们的数据集D有4条记录，分别是134,235,1235和25。现在我们用Apriori算法来寻找频繁k项集，最小支持度设置为50%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235，现在我们链接生成候选频繁2项集，包括12,13,15,23,25,35共6组。此时我们的第一轮迭代结束。
　　　　进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于12和15的支持度只有25%而被筛除，得到真正的频繁2项集，包括13,23,25,35。现在我们链接生成候选频繁3项集,123, 135和235共3组，这部分图中没有画出（其实是因为12，15就是支持度不满足最小支持度，所以他们的超集一定不满足最小支持度，故不需要计算）。通过计算候选频繁3项集的支持度，我们发现123和135的支持度均为25%，因此接着被剪枝，最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集235。

4. 样例以及Python实现代码

下图是《数据挖掘：概念与技术》（第三版）中挖掘频繁项集的样例图解。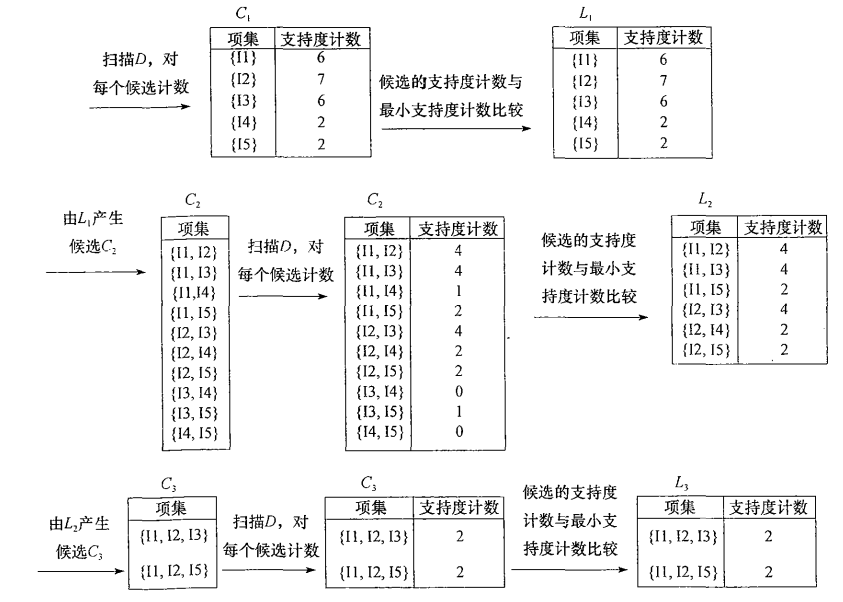

# Python 2.7
# Filename: apriori.py
# Author: llhthinker
# Email: hangliu56[AT]gmail[DOT]com
# Blog: http://www.cnblogs.com/llhthinker/p/6719779.html
# Date: 2017-04-16
def load_data_set():
    """
    Load a sample data set (From Data Mining: Concepts and Techniques, 3th Edition)
    Returns: 
        A data set: A list of transactions. Each transaction contains several items.
    """
    data_set = [['l1', 'l2', 'l5'], ['l2', 'l4'], ['l2', 'l3'],
            ['l1', 'l2', 'l4'], ['l1', 'l3'], ['l2', 'l3'],
            ['l1', 'l3'], ['l1', 'l2', 'l3', 'l5'], ['l1', 'l2', 'l3']]
    return data_set
def create_C1(data_set):
    """
    Create frequent candidate 1-itemset C1 by scaning data set.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
    Returns:
        C1: A set which contains all frequent candidate 1-itemsets
    """
    C1 = set()
    for t in data_set:
        for item in t:
            item_set = frozenset([item])
            C1.add(item_set)
    return C1
def is_apriori(Ck_item, Lksub1):
    """
    Judge whether a frequent candidate k-itemset satisfy Apriori property.
    Args:
        Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
                 candidate k-itemsets.
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
    Returns:
        True: satisfying Apriori property.
        False: Not satisfying Apriori property.
    """
    for item in Ck_item:
        sub_Ck = Ck_item - frozenset([item])
        if sub_Ck not in Lksub1:
            return False
    return True
def create_Ck(Lksub1, k):
    """
    Create Ck, a set which contains all all frequent candidate k-itemsets
    by Lk-1's own connection operation.
    Args:
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
        k: the item number of a frequent itemset.
    Return:
        Ck: a set which contains all all frequent candidate k-itemsets.
    """
    Ck = set()
    len_Lksub1 = len(Lksub1)
    list_Lksub1 = list(Lksub1)
    for i in range(len_Lksub1):
        for j in range(1, len_Lksub1):
            l1 = list(list_Lksub1[i])
            l2 = list(list_Lksub1[j])
            l1.sort()
            l2.sort()
            if l1[0:k-2] == l2[0:k-2]:
                Ck_item = list_Lksub1[i] | list_Lksub1[j]
                # pruning
                if is_apriori(Ck_item, Lksub1):
                    Ck.add(Ck_item)
    return Ck
def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
    """
    Generate Lk by executing a delete policy from Ck.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        Ck: A set which contains all all frequent candidate k-itemsets.
        min_support: The minimum support.
        support_data: A dictionary. The key is frequent itemset and the value is support.
    Returns:
        Lk: A set which contains all all frequent k-itemsets.
    """
    Lk = set()
    item_count = {}
    for t in data_set:
        for item in Ck:
            if item.issubset(t):
                if item not in item_count:
                    item_count[item] = 1
                else:
                    item_count[item] += 1
    t_num = float(len(data_set))
    for item in item_count:
        if (item_count[item] / t_num) >= min_support:
            Lk.add(item)
            support_data[item] = item_count[item] / t_num
    return Lk
def generate_L(data_set, k, min_support):
    """
    Generate all frequent itemsets.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        k: Maximum number of items for all frequent itemsets.
        min_support: The minimum support.
    Returns:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.
    """
    support_data = {}
    C1 = create_C1(data_set)
    L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
    Lksub1 = L1.copy()
    L = []
    L.append(Lksub1)
    for i in range(2, k+1):
        Ci = create_Ck(Lksub1, i)
        Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
        Lksub1 = Li.copy()
        L.append(Lksub1)
    return L, support_data
def generate_big_rules(L, support_data, min_conf):
    """
    Generate big rules from frequent itemsets.
    Args:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.
        min_conf: Minimal confidence.
    Returns:
        big_rule_list: A list which contains all big rules. Each big rule is represented
                       as a 3-tuple.
    """
    big_rule_list = []
    sub_set_list = []
    for i in range(0, len(L)):
        for freq_set in L[i]:
            for sub_set in sub_set_list:
                if sub_set.issubset(freq_set):
                    conf = support_data[freq_set] / support_data[freq_set - sub_set]
                    big_rule = (freq_set - sub_set, sub_set, conf)
                    if conf >= min_conf and big_rule not in big_rule_list:
                        # print freq_set-sub_set, " => ", sub_set, "conf: ", conf
                        big_rule_list.append(big_rule)
            sub_set_list.append(freq_set)
    return big_rule_list
if __name__ == "__main__":
    """
    Test
    """
    data_set = load_data_set()
    L, support_data = generate_L(data_set, k=3, min_support=0.2)
    big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
    for Lk in L:
        print "="*50
        print "frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport"
        print "="*50
        for freq_set in Lk:
            print freq_set, support_data[freq_set]
    print
    print "Big Rules"
    for item in big_rules_list:
        print item[0], "=>", item[1], "conf: ", item[2]

运行结果：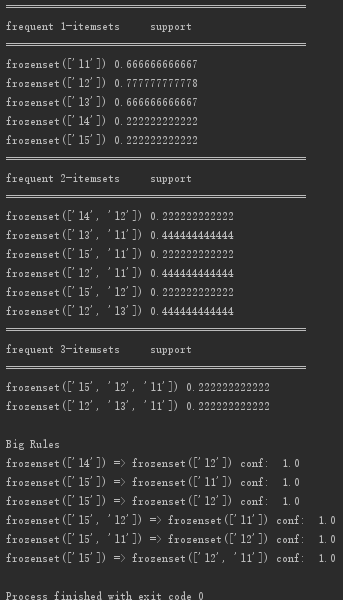

5、关联算法特点

关联规则是一种有效且很重要的数据挖掘方法，它可以从海量数据中挖掘出数据之间有意义的关联规则及它们之间的相关联系，帮助相关人员分析数据并做出合适的决策；其最典型的应用例子是购物车分析，即通过分析顾客放入购物车中的商品来分析顾客的购买习惯，从而指导零售商制定更好的营销策略。
目前常用的关联规则方法有很多，如贝叶斯网络、决策树、Apriori算法等。其中Apriori算法是关联规则挖掘频繁项集的经典算法，最早由R.Agrawal等人在1993年提出来的，是一种挖掘单维布尔型的关联规则算法，很多算法也是以其为核心进行改进的。**
Apriori算法是关联规则挖掘最经典的方法，该算法的优点在于使用先验性质，大大提高了频繁项集逐层产生的效率，算法本身无复杂推导，简单易理解，同时对数据集要求低，因此得到了广泛的应用。但是算法也存在缺点：当事务数据库很大时，候选频繁k项集数量巨大；在验证候选频繁k项集的时候，需要对整个数据库进行扫描，非常耗时。

6、单维关联与多维关联规则

基于规则中涉及到的数据的维数,关联规则可以分为单维的和多维的。

• 单维关联规则：处理单个维中属性间的关系，即在单维的关联规则中，只涉及到数据的一个维。 例如，用户购买的物品：“咖啡=>砂糖”，这条规则只涉及到用户的购买的物品。
• 多维关联规则：处理多个维中属性之间的关系，即在多维的关联规则中，要处理的数据将会涉及多个维。例如，性别=“女”⟹职业=“秘书”，这条规则就涉及到两个维中字段的信息，是两个维上的一条关联规则。