CVPR2020 接收的论文已经可以下载了,解读一篇之前有放在 ArXiv 的论文Bi3D: Stereo Depth Estimation via Binary Classifications,利用多个二分类器进行深度 / 视差估计。这里首先讨论本文提出方法的原理,它的优势将在最后和实验一起介绍。
利用视差向量的方向判断深度值与某一深度平面的远近关系
我们知道,在校正好的双目图像中,同一世界点在左图的水平像素坐标大,在右图的水平像素坐标小(即同一物体在左图靠右,在右图靠左)。那么对于左图中的某个点,要寻找到它在右图中的对应点,就要向左移位,即视差向量的方向是水平向左的,如下图 (b)(c) 所示。

现在,我们用某一深度值为
的深度(视差)平面对右图进行投影到左视角,那么右图中所有的点都会水平向右移位一些像素。此时,变换后的右图(Warped R)再去与左图寻找对应点时,就会有了一些新的现象。比如图中小鳄鱼,它的深度值比较小,即左右图中对应的视差比较大,当用
这一深度值大于小鳄鱼深度的平面投影时,对应的移位就小于原来的视差。那么投影之后,仍是左图的点靠右,变换后右图的点靠左,视差的方向仍是水平向左。而对于较远处的小鹿来说,它本身的视差比较小,变换右图时它向右移位超过了它原本的视差值,这个时候左图的点再去对应到变换右图的点时,视差的方向就变成水平向右了,如上图 (d)(e)。在文中,上面这个图是动图,可以查看原文加深理解。
也就是说,我们用某一深度平面变换右图之后,对于任意一点,如果能知道它的视差向量方向,就可以判断这个点的深度值是大于该深度平面还是小于该深度平面了。本文中,这一思路用网络(二分类器)来学习,输入左右图和深度平面,输出一张置信度图。置信度越接近 1,越有把握认为该点深度值大于深度平面深度值;置信度越接近 0,越有把握认为该点深度值小于深度平面深度值。
下图即二分类器的网络。SegNet 是一个 encoder-decoder 的结构,输入的是左图特征 + 变换右图特征,输出利用左图特征调优一下(图里没画),最终由 softmax 得到输出的置信度图。

假设我们现在已经对要解析的场景确定了多个深度平面,对应地,我们获得了多张置信度图。现在,我们要获得深度(视差)图了。首先,将置信度图按照深度从小到大进行串联。然后,对于每个像素点,画一条置信度关于深度的曲线,如下图 (b),这里图的横轴纵轴反了,应该是纵轴是 C 表示置信度,横轴是 d 表示深度。
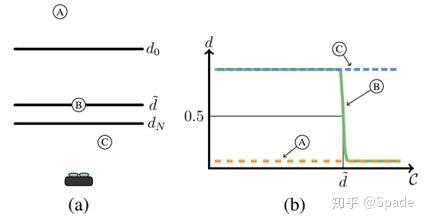
根据之前置信度的定义,置信度 0.5 附近时,应该是该点深度与这一深度平面接近。相比于直接寻找 C=0.5 的深度值,采用曲线下面积计算深度,更加鲁棒。由于我们这里是离散的多个深度平面,曲线下面积即通过求和实现。
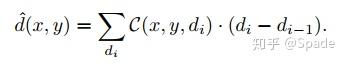
粗略的深度估计
二分类器估计的置信度与某点深度值的概率存在关系,即:
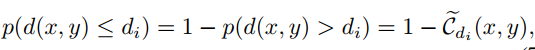
这种关系使得我们可以确定某点深度值在某一深度范围内的概率:
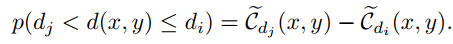
我们可以简单地找到最大概率的深度范围,然后取这个深度范围的平均值,当作该点深度。这是一种粗略地估计深度的思路。
精细的深度估计
本文又设计了一个精细化预测深度的模块。如果定义了 N 个深度平面,就可以利用刚刚训练的二分类器模块 SegNetBlock 得到多张输出(这里还不是置信度,要 softmax 之后才是)。类似于其他立体匹配模型中的 cost volume,这里也是一个 3D 的 tensor(HWN)。利用 3D 卷积(RegNet)可以调优,最终用 softmax 得到 N 张置信度图,用 AUC 计算得到深度图之后,再用一个调优模块,得到最终的输出。
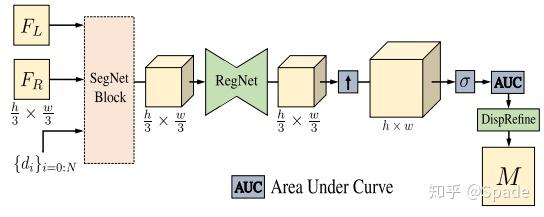
训练:
我们自己划分深度平面,随后利用视差真值,即可给出置信度真值图(只有 0/1)。可以利用二进制交叉熵损失训练估计置信度。视差结果可以用普通的 L1/L2 损失。
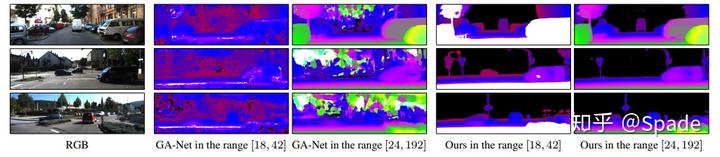
方法优势:
- 根据需求平衡速度与深度预测的精度。以壁障为例,比较远的物体,不需要太精细的深度预测,而比较近的距离则最好提供更高的精度。

- 可以在不同深度范围测试。其他立体匹配模型的视差范围都是提前确定好的,本文的方法可以自由设定一些深度平面。