TypeScript

Ts 中的 unsoundness

https://effectivetypescript.com/2021/05/06/unsoundness/

Book

JS 二十年

https://cn.history.js.org/part-1.html#%E8%BF%B7%E6%83%91%E8%A1%8C%E4%B8%BA%E4%B8%8E-bug

SICP

Tree Recursion

树递归
Another common pattern of computation is called tree recursion.
典型的斐波拉契

function fib(n) {
    return n === 0
           ? 0
           : n === 1
           ? 1
           : fib(n - 1) + fib(n - 2);
}

This function is instructive as a prototypical tree recursion, but it is a terrible way to compute Fibonacci numbers because it does so much redundant computation.
这样的斐波拉契计算是糟糕的，因为有太多冗余，如fib3被整个重复执行了两次
改为迭代方式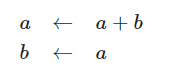

function fib(n) {
    return fib_iter(1, 0, n);
}
function fib_iter(a, b, count) {
    return count === 0
           ? b
           : fib_iter(a + b, a, count - 1);
}

One should not conclude from this that tree-recursive processes are useless. When we consider processes that operate on hierarchically structured data rather than numbers, we will find that tree recursion is a natural and powerful tool.
树递归更适合操作分层结构数据时，更加自然且强大

另一个例子

eg：Counting change

How many different ways can we make change of $1.00, given dollars, half-dollars, quarters, dimes, nickels, and pennies? More generally, can we write a function to compute the number of ways to change any given amount of money
在给定 1美元，50美元，25美分，10美分，5美分 的情况下，我们可以用多少种不同的来兑换 n 美元？ 更笼统地说，我们可以编写一个函数来计算更改任何给定金额的方法的数量吗？
1 美元 = 100 美分
The number of ways to change amount a using n kinds of coins equals

• the number of ways to change amount a using all but the first kind of coin, plus
• the number of ways to change amount a − d using all n kinds of coins, where d is the denomination of the first kind of coin.

利用分治法将 6 种硬币 兑换 n 美元这个问题分成两个小问题：

1. 除了第一种硬币，使用其他硬币来兑换成 n 美元；
2. 必须使用第一种硬币，也就是 使用其他硬币，兑换 n 美元 - 第一种硬币面额；

如下可得：

function count_change(amount) {
    return cc(amount, 6);
}
function cc(amount, kinds_of_coins) {
    return amount === 0
           ? 1
           : amount < 0 || kinds_of_coins === 0
           ? 0
           : cc(amount, kinds_of_coins - 1)
             +
             cc(amount - first_denomination(kinds_of_coins),
                kinds_of_coins);
}
function first_denomination(kinds_of_coins) {
    return kinds_of_coins === 1 ? 1 :
           kinds_of_coins === 2 ? 5 :
           kinds_of_coins === 3 ? 10 :
           kinds_of_coins === 4 ? 25 :
           kinds_of_coins === 5 ? 50 :
           kinds_of_coins === 6 ? 100 : 0;
}

One approach to coping with redundant computations is to arrange matters so that we automatically construct a table of values as they are computed. Each time we are asked to apply the function to some argument, we first look to see if the value is already stored in the table, in which case we avoid performing the redundant computation. This strategy, known as tabulation or memoization, can be implemented in a straightforward way. Tabulation can sometimes be used to transform processes that require an exponential number of steps (such as countchange) into processes whose space and time requirements grow linearly with the input.
在计算的同时维护一个值表，计算前先查看值是否已存在，这种策略叫做 tabulation or memoization
所以树递归配合缓存的方式，能很好地描述演化过程，又能有效避免冗余计算，_可用于将需要指数级步数（如计数变化）的过程转换为空间和时间要求随输入线性增长的过程。