0 引言
世界坐标系下的点如何投影到 CCD 镜头上,通过成像的方式得到点在二维图像上的像素坐标值,这是摄影测量中的一个基础而核心的问题。这个问题中核心的东西有两个:1、坐标系的定义及其空间转换矩阵 2、成像中的误差 下面将从这两个角度对这个问题进行详细探讨。文章参考了
# 陈建平: 《相机成像原理》PPT
https://blog.csdn.net/chentravelling/article/details/53558096
# 《StereoVision》
http://vision.deis.unibo.it/~smatt/Seminars/StereoVision.pdf
另外还有《学习 opencv》以及《计算机视觉中的多视图几何》,如有错误欢迎探讨。
1 相机投影中的坐标系及其转换关系
在《相机成像原理》中,陈建平指出图像处理涉及到四个坐标系,如下图所示。
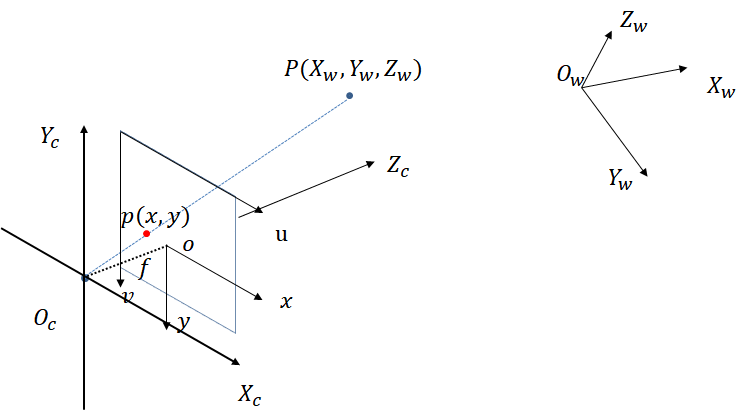

(1)世界坐标系与相机坐标系
从世界坐标系到相机坐标系属于刚体变换,即物体不会发生形变,只需要进行旋转和平移(RT),此为相机的外参矩阵。
在张正友标定法中,将世界坐标系的原点设定在棋盘格的左上角点,Z 轴垂直于棋盘平面(XOY 平面);相机坐标系的原点在相机光心,Z 轴在光轴上,垂直于成像平面。
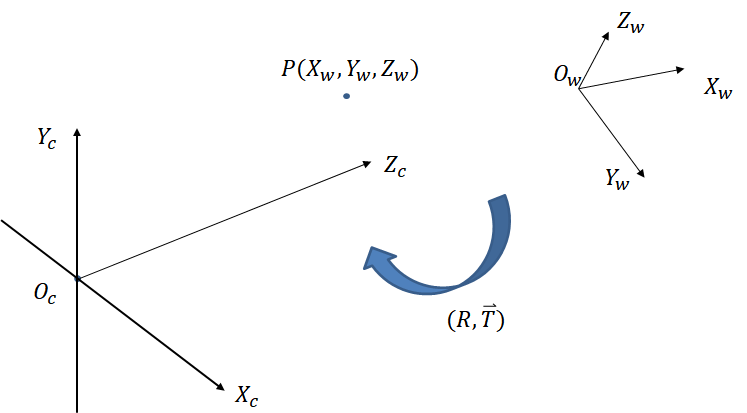
(2)相机坐标系与图像坐标系:称为摄像机模型以及投影矩阵
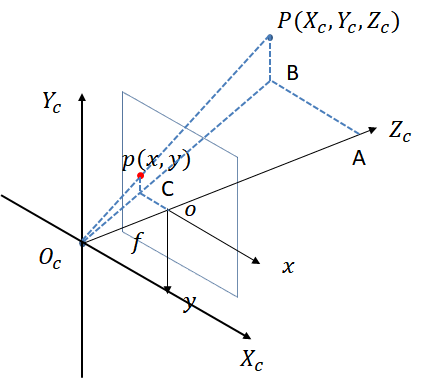
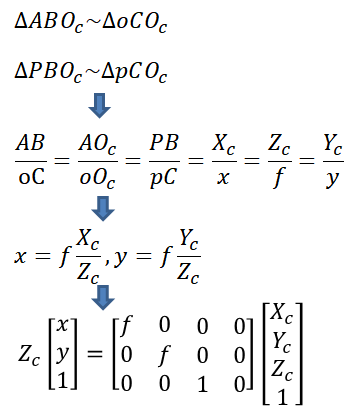
(3)图像坐标系与像素坐标系
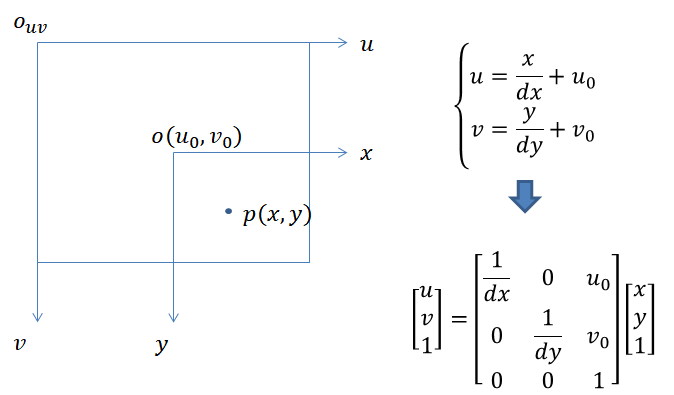
(4)从世界坐标系到像素坐标系的转换方程
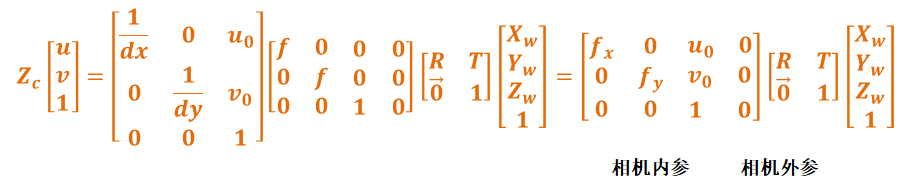
其中,f 为相机焦距,1/dx (pixel/mm)和 1/dy(pixel/mm) 为图像坐标系到像素坐标系的转换因子,考虑相机加工时每个成像单元不完全为矩形,因此在 x 和 y 方向采用了不同的比例尺进行转换。
(5)综述
以棋盘为例,可以棋盘的左上角点为原点,横向为 X 轴,纵向为 Y 轴,垂直方向为 Z 轴方向建立世界坐标系。这个坐标系是目标物体的自有坐标系,可以用来描述相机的位置,作为双目视觉系统的参考系,从而求出相机之间的相对关系。如果选择左相机的光心和光轴建立世界坐标系,则左相机的相机坐标系和世界坐标系重合,右相机和左相机的相对位置关系可以很轻易地描述出来。以每个相机拍摄出来的照片的中心位置为基准建立的图像坐标系是一个二维的坐标系。而表示在 opencv 中的像素坐标采用的是像素坐标系,这两个坐标之间存在一个(u0,v0)的偏差。
2 成像中的误差
(1)光芯偏移误差与单像素点矩形(非正方形)误差
通常来说,芯片的中心不在光轴上,因此我们引入两个新的参数 cx 和 cy,对可能的偏移进行建模;
在应对单像素点非正方形时,引入 1/dx (pixel/mm)和 1/dy(pixel/mm) 为图像坐标系到像素坐标系在 x 和 y 方向上的转换因子。
得到的内参转换矩阵为:
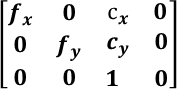
相比于上面的相机内参矩阵,在参数数量上没有发生变化,只不过含义发生了变化,因此不影响求解过程。通常采用张正友标定发求解这部分误差(opencv)
(2)透镜畸变
优点:利用透镜收集更多的光线;
缺点:背离了针 孔几何模型,而且引入透镜的畸变。
畸变是透镜固有的特性,凸透镜汇聚光线,凹透镜发散光线,所以无法消除,只能改善。
主要包括径向和切向畸变,是一个五维的畸变参数向量。径向畸变来自于透镜形状,而切向畸变则来自于整个摄像机的组装过程。
径向畸变包括桶形畸变和枕形畸变,通常表现为远离透镜中心的光线弯曲比靠近中心的严重。之所以在加工透镜时要引入该畸变是为了压缩透镜体积,并且增加通光量,扩大透镜的视角,让透镜看到更多东西。
切向畸变是由于透镜制造上的缺陷,使得透镜本身与图像平面不平行而产生的。通常采用 brown 的方法求解这部分误差(opencv)
3 相机标定过程中的内参、外参与畸变参数求解
这部分主要参考了《学习 opencv》与《计算机视觉中的多视图几何》. 求解相机内外参数的过程称为标定,有自标定和基于标定板两种方式。
(1)平面单应性矩阵求解
在计算机视觉中,平面的单应性被定义为从一个平面到另一个平面的投影映射,如图所示。
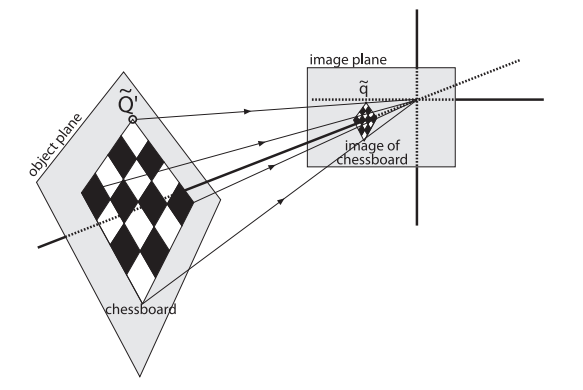
因此,一个二维平面上的点映射到摄像机成像仪上,就是平面单应性的例子。以张正友标定法中的棋盘格为例,通过拍摄一组在小范围内变换姿态的棋盘格,可以获得一组单应矩阵,可以解决以下问题。
1、表述真实世界中一个平面与对应它图像的透视变换:从世界坐标系到像素坐标系。
2、通过透视变换实现图像从一种视图变换到另外一种视图
因此,单应性矩阵描述了从物体平面到图像平面的映射,同时表征了这两个平面的的相对位置(物理变换)以及摄像机投影矩阵(内参矩阵投影变换)。
其数学表示形式如下。
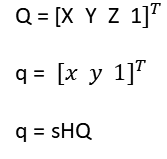
其中, Q 为点在世界坐标系下的点,在标定时,建立以棋盘格的左上角点定义为原点,垂直方向定义为 Z 轴的世界坐标系;
q 为点做像素坐标系下的点,s 为尺度转换因子,通常根据习惯放在 H 的外面;
H 为单应性矩阵,H = M * W 为内参矩阵与外参矩阵的乘积。
M = 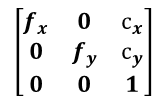
, W = [R T] ,是 3*4 矩阵
为了简化求解过程,把世界坐标系构造在 Z=0 的平面上; 此时,其中一个列变量就不需要了,H 也从 34 的矩阵被简化为 33 矩阵。这个过程的数学描述如下。
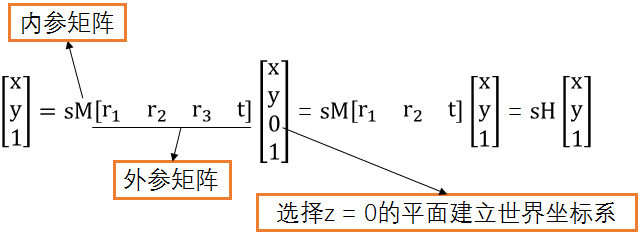
opencv 使用上述公式来计算单应性矩阵。它使用同一个物体的多个图像来计算每个视场的旋转和平移,同时也计算摄像机的内参数(对所有视场不变)。
(2)棋盘角点个数和参数个数
K 个棋盘图像,每个图像 N 个角点,在求解时的为了得到结果,约束的数量必须大于求解参数的数量。方程如下:
2 N K > 6 * K + 4 // 2 表示每个像素角点有两个坐标(x, y), 6K 表示 K 幅图像有 6K 这么多个外参数, 4 表示内参矩阵,固定不变
在实际使用中,为了得到高质量结果,通常会使约束的数量足够大,比如采用 10 幅 7* 8 的左右视图解单应矩阵,则上述不等式为
2 78 10 > 6 10 + 4 即 1120 > 64
采用非线性最小二乘优化方法即可解得单应性矩阵。
(3)单应性矩阵分解得到内外参矩阵
QR 分解,将满秩的单应矩阵分解得到一个上三角阵和一个正交阵;为了保证唯一性,可以令
1、图像的 X/Y 轴所指方向与相机的 X/Y 轴方向相同
2、相机处于 z 轴正方向
可以得到唯一解。
(4)畸变参数求解
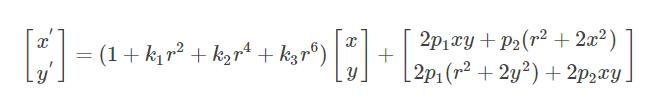
其中,[x′,y′]为畸变矫正后的位置,[x,y]为畸变前的位置,[ki,pi][ki,pi]为畸变系数。
4 单目标定与双目标定
(1)单目标定
参考以下链接
https://www.cnblogs.com/zhazhiqiang2018/p/9537663.html#_Toc3638
(2)双目标定
参考以下链接
https://www.cnblogs.com/zhazhiqiang2018/p/9538986.html
(3)单双目视觉标定的不同点
单目标定的结果是一组摄像机内参矩阵、畸变参数和与图像数量相同的外参矩阵;
双目标定的结果是在每个相机单目标定的基础上,进而推算两个相机之间的变换矩阵。即两组摄像机内参矩阵、畸变参数和一个右相机到左相机的变换矩阵。
https://www.cnblogs.com/ghjnwk/p/10852264.html

