总时间限制: 2000ms 单个测试点时间限制: 500ms 内存限制: 65536kB

描述

在韩国，有一种小的青蛙。每到晚上，这种青蛙会跳越稻田，从而踩踏稻子。农民在早上看到被踩踏的稻子，希望找到造成最大损害的那只青蛙经过的路径。每只青蛙总是沿着一条直线跳越稻田，而且每次跳跃的距离都相同。

稻子组成一个栅格，每棵稻子位于一个格点上。而青蛙总是从稻田的一侧跳进稻田，然后沿着某条直线穿越稻田，从另一侧跳出去

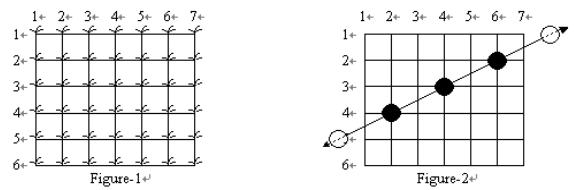
如下图所示，可能会有多只青蛙从稻田穿越。青蛙的每一跳都恰好踩在一棵水稻上，将这棵水稻拍倒。有些水稻可能被多只青蛙踩踏。当然，农民所见到的是图4中的情形，并看不到图3中的直线，也见不到别人家田里被踩踏的水稻。

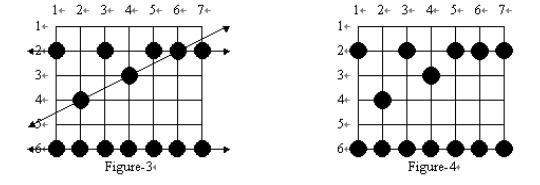
构造出青蛙穿越稻田时的行走路径，并且只关心那些在穿越稻田时至少踩踏了3棵水稻的青蛙。因此，每条青蛙行走路径上至少包括3棵被踩踏的水稻。而在一条青蛙行走路径的直线上，也可能会有些被踩踏的水稻不属于该行走路径

1. 不是一条行走路径：只有两棵被踩踏的水稻；
2. 是一条行走路径，但不包括（2，6）上的水道；
3. 不是一条行走路径：虽然有3棵被踩踏的水稻，但这三棵水稻之间的距离间隔不相等。

请你写一个程序，确定：在一条青蛙行走路径中，最多有多少颗水稻被踩踏。例如，图4的答案是7，因为第6行上全部水稻恰好构成一条青蛙行走路径。

输入

从标准输入设备上读入数据。第一行上两个整数R、C，分别表示稻田中水稻的行数和列数，1≤R、C≤5000。第二行是一个整数N，表示被踩踏的水稻数量， 3≤N≤5000。在剩下的N行中，每行有两个整数，分别是一颗被踩踏水稻的行号(1~R)和列号(1~C)，两个整数用一个空格隔开。而且，每棵被踩踏水稻只被列出一次。

输出

从标准输出设备上输出一个整数。如果在稻田中存在青蛙行走路径，则输出包含最多水稻的青蛙行走路径中的水稻数量，否则输出0。

样例输入

6 7
14 
2 1 
6 6 
4 2 
2 5 
2 6 
2 7 
3 4 
6 1 
6 2 
2 3 
6 3 
6 4 
6 5 
6 7

样例输出

7

思路

我们枚举路径开始的2个点，由于两点确定一条直线，当开始的2个点被确定下来后，后面的很多因素也就被定下来了。

假设一只青蛙进入稻田后踩踏的前2个水稻分别是 #card=math&code=%28x_1%2C%20y_1%29)#card=math&code=%28x_2%2C%20y_2%29)

• 青蛙下一跳的步长为：

  • X方向：
  • Y方向：
• #card=math&code=%28x_1%20-%20dx%2C%20y_1%20-%20dy%29) 必须落在稻田外;
• 当青蛙在水稻田某一位置#card=math&code=%28x%2C%20y%29)上时，下一跳踩踏的水稻坐标为：#card=math&code=%28x%20%2B%20dx%2C%20y%20%2B%20dy%29)
• 将路径上的最后一棵水稻记作 #card=math&code=%28x_k%2C%20y_k%29)，#card=math&code=%28x_k%20%2B%20dx%2C%20y_k%20%2B%20dy%29) 需要落在稻田之外.

枚举的过程我们这样操作：

• 从输入的水稻中任取2棵，作为一只青蛙进入水稻后踩踏的前2棵水稻，看能否形成一条穿越稻田的路径

为了降低搜索空间，我们需要排除错误的答案。猜测 #card=math&code=%28X_1%2C%20Y_1%29)#card=math&code=%28X_2%2C%20Y_2%29)

1. 青蛙不能经过一跳从稻田外跳到 #card=math&code=%28X_1%2C%20Y_1%29)上；
2. 按照 #card=math&code=%28X_1%2C%20Y_1%29), #card=math&code=%28X_2%2C%20Y_2%29) 确定的步长，从 #card=math&code=%28X_1%2C%20Y_1%29) 出发，青蛙最多经过 #card=math&code=%28MAXSTEPS%20-%201%29) 步，就会跳到稻田之外, 其中 是当前已经找到的最好答案.

我们用面向对象的类来描述一个坐标点，并借助C++提供的函数来帮助我们简化代码。

代码

样例数据能得到答案，但是不知道为什么POJ没过。。。。

#include <iostream>
#include <algorithm>
using namespace std;
class Plant {
public:
    int x, y;
};
Plant plants[5001];
int row = 0, col = 0, totalRice;
int searchPath(Plant secarchPlant, int dx, int dy) {
    /* 判断从 searchPlant 开始，步长为 dx, dy, 那么最多能走几步 */
    Plant myPlant;
    myPlant.x = secarchPlant.x + dx;
    myPlant.y = secarchPlant.y + dy;
    int step = 2;
    while( myPlant.x <= row && myPlant.x >= 1 && myPlant.y <= col && myPlant.y >= 1 ) {
        if( !binary_search(plants, plants + totalRice, myPlant) ) {
            step = 0;
            break;
        }
        myPlant.x += dx;
        myPlant.y += dy;
        step++;
    }
    return step;
}
bool operator < (const Plant& p1, const Plant& p2) { // 配合sort函数
    if( p1.x == p2.x )  return p1.y < p2.y;
    return p1.x < p2.x;
}
int main() {
    cin >> row >> col >> totalRice;
    for(int i = 0; i < totalRice; i++)
        cin >> plants[i].x >> plants[i].y;
    // 将水稻按x坐标从小到大排序, x坐标相同按y从小到大排序
    sort(plants, plants + totalRice);  
    // 枚举每一个点
    int max = 0, steps = 0;
    for(int i = 0; i < totalRice - 2; i++) {  // plants[i]是第一个点
        for(int j = i + 1; j < totalRice - 1; j++) {  // plant[j]是第二个点
            int dx = plants[j].x - plants[i].x;
            int dy = plants[j].y - plants[i].y;
            int previousX = plants[i].x - dx;
            int previousY = plants[i].y - dy;
            if(previousX <= row && previousX >= 1 && previousY <= col && previousY >= 1)
                continue;  // 第2个点选的不合适
            if( plants[i].x + (max - 1) * dx > row )
                break;  // 第1个点选的不合适
            previousY = plants[i].y + (max - 1) * dy;
            if( previousY > col || previousY < 1 ) 
                continue;  // Y方向过早越界
            steps = searchPath(plants[j], dx, dy);
            if(steps > max)  max = steps;
        }
    }
    if( max == 2)  cout << 0 << endl;
    else  cout << max << endl;
    return 0;
}