路径总和Ⅱ-47

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

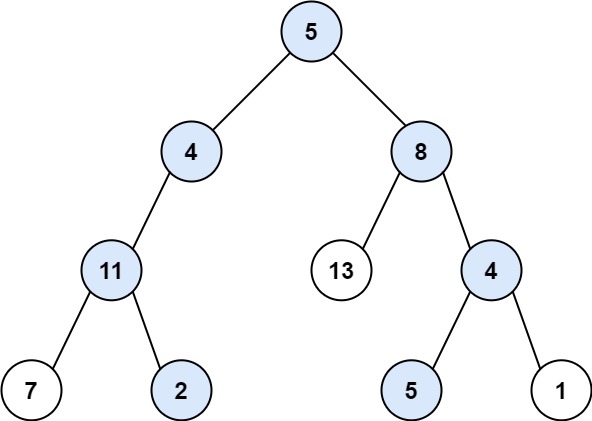
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]

示例 2：

Input: root = [1,2,3], targetSum = 5
Output: []

示例 3：

Input: root = [1,2], targetSum = 0
Output: []

提示：

• -1000 ≤ Node.val ≤ 1000
• -1000 ≤ targetSum ≤ 1000
• 树中节点总数在范围 [0, 5000] 内

思路

先把根节点加入到path，然后进行左递归的DFS。

递归终止条件：访问到叶子节点（没有左右子树的节点）。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> answer;
        if( root == nullptr )   return answer;
        vector<int> path;
        path.emplace_back( root->val );
        targetSum -= root->val;
        dfs(root, targetSum, answer, path);
        return answer;
    }
    void dfs(TreeNode* node, int targetSum, vector<vector<int>>& answer, vector<int>& path) {
        // 1. Exit condition: leaf node
        if( node->left == nullptr && node->right == nullptr ) {
            if( 0 == targetSum ) {
                answer.emplace_back( path );
                return;
            }
        }
        // 2. Walk every node that not visited
        if( node->left != nullptr ) {
            path.emplace_back( node->left->val );
            dfs( node->left, targetSum - node->left->val, answer, path );
            path.pop_back();
        }
        if( node->right != nullptr ) {
            path.emplace_back( node->right->val );
            dfs( node->right, targetSum - node->right->val, answer, path );
            path.pop_back();
        }
    }
};