长度最小的子数组-209

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [nums, nums, …, nums, nums] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

示例 2：

Input: target = 4, nums = [1,4,4]
Output: 1

示例 3：

Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

提示：

• 1 ≤ target ≤ 10；
• 1 ≤ nums.length ≤ 10；
• 1 ≤ nums[i] ≤ 10
• 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

思路

本题有两个思路，一个是暴力穷举，一个是滑动窗口（类似于双指针）。

对于滑动窗口，借用代码随想录的示意图：

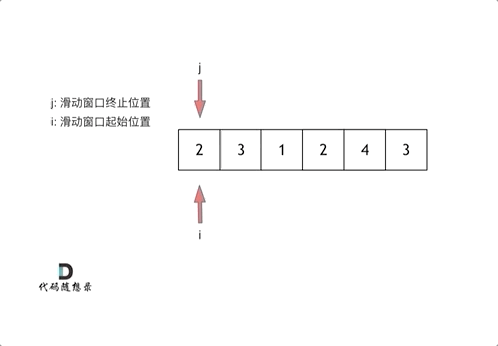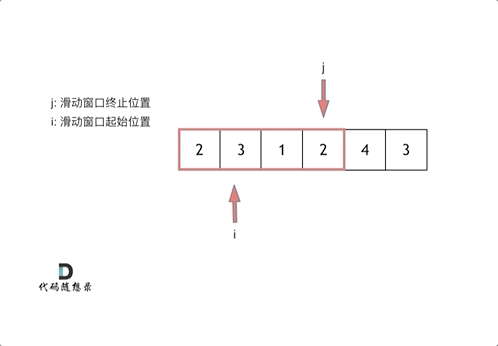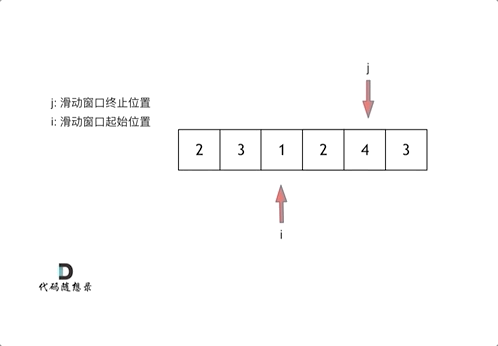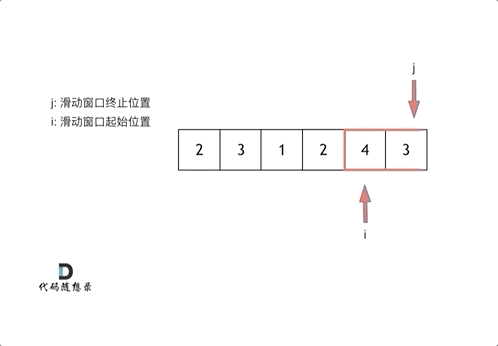
我们新建两个指针，一个start指向起点，一个end指向终点。两个指针构成的闭区间就是我们所说的窗口。

当区间的序列和 ≥ target时，我们就要把start指针向右移动。

如果最后start和end重合，且指向的值不是target，则我们认为找不到长度最小的子数组，返回0。

代码

Cpp：

// 4ms, 10.2MB
class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int start = 0, end = 0;
        unsigned cur_sum = 0;
        unsigned window_size = 0;
        unsigned result = 0xf << 15;
        for(end = 0; end < nums.size(); end++) {
            cur_sum += nums[end];
            while( cur_sum >= target ) {
                window_size = (end - start + 1);
                result = result < window_size ? result : window_size;
                cur_sum -= nums[start];
                start += 1;
            }
        }
        return (result == 0xf << 15 ? 0 : result);
    }
};

Rust：

// 0ms, 2.3MB
impl Solution {
    pub fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
        let mut start = 0;
        let mut end = 0;
        let mut cur_sum = 0;
        let mut windows_size = 0;
        let mut result = 0xf << 15;
        while end < nums.len() {
            cur_sum += nums[end];
            while cur_sum >= target {
                windows_size = (end - start + 1);
                result = if result < windows_size {
                    result
                } else {
                    windows_size
                };
                cur_sum -= nums[start];
                start += 1;
            }
            end += 1;
        }
        if result != 0xf << 15 {
            result as i32
        } else {
            0
        }
    }
}