括号生成-22

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

示例 2：

Input: n = 1
Output: ["()"]

提示：

• 1 ≤ n ≤ 8

思路

本题可构建一棵求解树，如下图所示：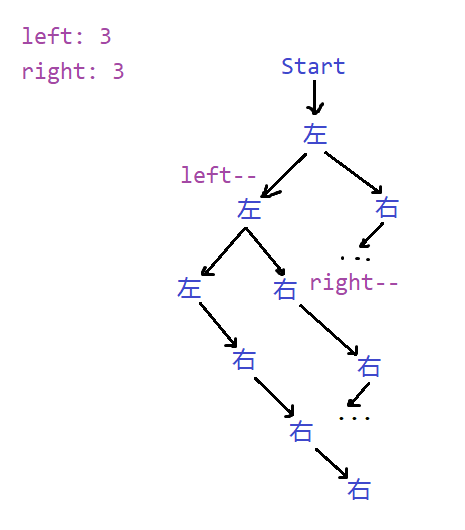

分析题目我们可以发现，在合法的括号中，第一个不能是右括号，或者说，当左括号的个数和右括号的个数相等时，我们不能选右括号。

DFS需要一个终止递归的条件，本题的终止条件是什么呢？因为括号是成对出现的，所以当path的长度等于2 * n时，我们就停止递归。例如n=3，那最终会生成长度为2 * 3 = 6的字符串。

我们分别为做左括号和右括号维护一个计数器。这个计数器的功能类似于bool[] visited数组。

代码

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        vector<string> answer;
        if(n == 0)   return answer;
        if(n == 1) {
            answer.emplace_back( "()" );
            return answer;
        }
        int* visited = new int[n];
        for(int i = 0; i < n; i++)   visited[i] = n;
        string path;
        string token = "()";
        dfs(n, answer, token, visited, path);
        delete[] visited;
        return answer;
    }
    void dfs
    (
        const int n,
        vector<string>& answer,
        const string& token,
        int visited[],
        string& path
    ) {
        // 1. Exit condition
        if( path.size() == 2 * n ) {
            answer.emplace_back( path );
            return;
        }
        // 2. Walk every node that not visited
        if( visited[0] > 0 ) {
            string node = path + token[0];
            visited[0]--;
            dfs(n, answer, token, visited, node);
            visited[0]++;
        }
        if( visited[1] > 0 && visited[0] != visited[1] ) {
            string node = path + token[1];
            visited[1]--;
            dfs(n, answer, token, visited, node);
            visited[1]++;
        }
    } 
};