组合总和-39

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合

示例 1：

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

示例 2：

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

Input: candidates = [2], target = 1
Output: []

示例 4：

Input: candidates = [1], target = 1
Output: [[1]]

示例 5：

Input: candidates = [1], target = 2
Output: [[1,1]]

提示：

• 1 ≤ candidates.length ≤ 30
• 1 ≤ candidates[i] ≤ 200
• candidate 中的每个元素都是独一无二的。
• 1 ≤ target ≤ 500

思路

本题可构建一棵树，如下图所示：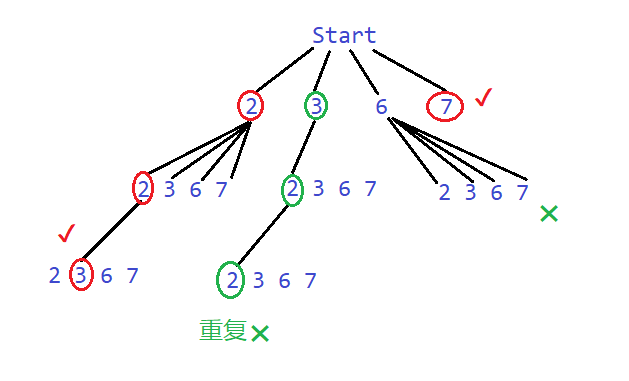

由于每次都可以出一样的数，所以我们没必要维护bool[] visited数组了。去重是一个难点，安装普通的深度优先搜索算法，能求出所以排列，但是找组合，我们需要用到STL的容器set。

我们在DFS时，传入一个set，在每次搜索到终止条件时，对当前找到的路径path进行一次排序，然后再加入到set里。set是不包含重复元素的，我们能自动完成去重任务。

最后我们再把set的内容抄到vector< vector<int> >数组里，返回出去。

初始AC代码的效率比较低的，一个原因是没有剪枝；另一个原因是我们对path反复求和，这里头包含很多重复计算。

一个改进的方法，就是把target弄成一个变化的值。在每次DFS时，只需要判断node - target是否等于0即可。改进后的AC代码效率稍微高了一点点。

代码

class Solution {  // 初始AC代码, 148ms
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector< vector<int> > result;
        if( candidates.size() == 0 )   return result;
        if( candidates.size() == 1 ) {
            if( candidates[0] > target )   return result;
            if( candidates[0] == target ) {
                result.push_back( candidates );
                return result;
            }
        }
        vector<int> path;
        set< vector<int> > result_set;
        dfs(candidates, target, result_set, path, 0);
        for(auto it = result_set.begin(); it != result_set.end(); it++) {
            result.push_back( *it );
        }
        return result;
    }
    void dfs
    (
        vector<int>& candidates, 
        int target, 
        set< vector<int> >& result_set, 
        vector<int>& path,
        int current_sum
    ) {
        // 1. Exit condition
        if( current_sum >= target ) {
            if( current_sum == target ) {
                vector<int> tmp = path;         // it's a must
                sort(tmp.begin(), tmp.end());
                result_set.insert( tmp );
            }
            return;
        }
        // 2. Walk every node that not visited
        for(int i = 0; i < candidates.size(); i++) {
            int node = candidates[i];
            path.push_back( node );
            dfs(candidates, target, result_set, path, calculate_sum(path));
            path.pop_back();
        }
    }
    int calculate_sum(vector<int>& nums) {
        int sum = 0;
        for(int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        return sum;
    }
};

// 改进后的AC代码，76ms
class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector< vector<int> > result;
        if( candidates.size() == 0 )   return result;
        if( candidates.size() == 1 ) {
            if( candidates[0] > target )   return result;
            if( candidates[0] == target ) {
                result.push_back( candidates );
                return result;
            }
        }
        vector<int> path;
        set< vector<int> > result_set;
        dfs(candidates, target, result_set, path);
        for(auto it = result_set.begin(); it != result_set.end(); it++) {
            result.push_back( *it );
        }
        return result;
    }
    void dfs
    (
        vector<int>& candidates, 
        int target, 
        set< vector<int> >& result_set, 
        vector<int>& path
    ) {
        // 1. Exit condition
        if( 0 >= target ) {
            if( 0 == target ) {
                vector<int> tmp = path;
                sort(tmp.begin(), tmp.end());
                result_set.insert( tmp );
            }
            return;
        }
        // 2. Walk every node that not visited
        for(int i = 0; i < candidates.size(); i++) {
            int node = candidates[i];
            path.push_back( node );
            dfs(candidates, target-node, result_set, path);
            path.pop_back();
        }
    }
};