DFS知识点

从起点出发, 走过的点要做标记, 发现没有走过的点, 就随便挑一个往前走, 走不过了就回退, 此种路径搜索策略就被称为深度优先搜索, 简称”深搜”.

其实称为远度优先搜索更容易理解. 因为这种策略能往前走一步就往前走一步, 总是试图走得更远. 所谓远近(或深度), 就是以距离起点的步数来衡量的.

判断从V出发是否能走到终点

它的算法逻辑如下:

#include <iostream>
bool DFS(V) {
    if( V为终点 )
        return true;
    if( V为旧点 )
        return false;
    将V标记为旧点;
    对和V相邻的每个节点U {
        if( DFS(U) == true )
            return true;
    }
    return false;
}
int main() {
    将所有的点标记为新点;
    起点 = 1;  // 起点的节点号
    终点 = 8;  // 终点的节点号
    cout << DFS(起点);
    return 0;
}

判断从V出发是否能走到终点，如果能，要记录路径

算法逻辑如下：

#include <iostream>
Node path[MAX_LEN];        // MAX_LEN取节点总数即可
int depth;
bool DFS(V) {
    if( V为终点 ) {
        path[depth] = V;
        return true;
    }
    if( V为旧点 )
        return false;
    将V标记为旧点;
    path[depth] = V;
    ++depth;
    对和V相邻的每个节点U {
        if( DFS(U) == true )
            return true;
    }
    --depth;
    return false;
}
int main() {
    将所有点标记为新点;
    depth = 0;
    if( DFS(起点) ) {
        for(int i = 0; i <= depth; i++)
            cout << path[i] << end;
    }
    return 0;
}

深度优先遍历图上所有节点

算法逻辑如下：

DFS(V) {
    if( V是旧点 )
        return;
    将V标记为旧点;
    对和V相邻的每个点U {
        DFS(U);
    }
}
int main() {
    将所有的点标记为新点;
    while( 在图中能找到新点k )
        DFS(k);
    return 0;
}

图的表示方法

邻接矩阵

用一个二维数组G存放图, G[i][j]表示节点i和节点j之间边的情况.

遍历复杂度: O(n), n为节点数目.

邻接表

每个节点V对应一个一维数组(Vector), 里面存放从V连出去的边, 边的信息包含另一个顶点, 还可能包含边权值等.

遍历复杂度: O(n+e), n为节点数目, e为边数目.

• 根据图论基本定理(握手定理): 点度之和为边数的两倍.
• 当边的数目很多时, 邻接表会变得很大.
• 而我们研究的图多半是稀疏图, 边不会太多, 所有遍历起来复杂度比邻接矩阵低.
• 而稠密图的情况, 邻接表的遍历不比邻接矩阵占太多优势.

DFS例子

DFS可以被当成一种思维方式，当一个问题被抽象成图后，也可以用DFS去遍历图上的节点。

Example：
给定一个字符串，要求给出所有字符的全排列。
比如，输入字符串ABC，会输出ABC，ACB，BAC，BCA，CAB，CBA。

这个例子应该如何思考呢？观察下图：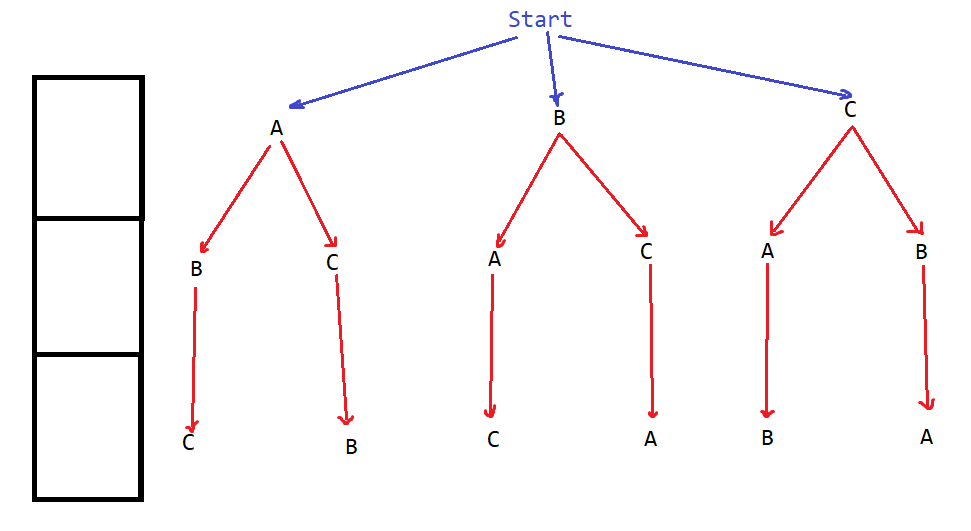

左边的三个格子代表三个坑位，第一个坑位有3中选择，到了第二个坑位，只剩2种选择，最后只剩一种。如果用图的观点去看，我们直接来一个深度优先遍历，就能得到我们的答案。

由于DFS是基于递归的，我们需要一个边界条件去终止。那边界条件是什么呢？
从第0层开始DFS，到 当前层数 和 输入字符串的长度相等 时，便终止递归。

我们还需要维护一个bool[] visited数组，里面的值意思是当前节点有没有被访问过。本例中visited是一维的，在后面的例子可能会有矩阵来存图，这时候visited就是二维的。

代码如下：

# input: a string, such as "ABC"
# output: All the permutation of input
def dfs(input_str, visited, level, output_str):
    # 1. exit condition
    if level == len(input_str):
        print("%s\n" % output_str)
        return
    # 2. walk all the node that not visited
    for i in range( len(input_str) ):
        node = input_str[i]
        if( visited[i] == False ): 
            output_str.append(node)
            visited[i] = True
            dfs(input_str, visited, level+1, output_str)
            visited[i] = False
            output_str.pop()
# --------
if __name__ == '__main__':
    input_str = "ABC"
    output_str = []
    visited = [False, False, False]
    dfs(input_str, visited, 0, output_str)

输出结果如下：