求根节点到叶节点数字之和-129

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

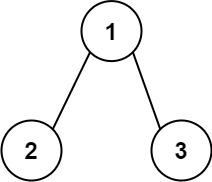
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

示例 2：

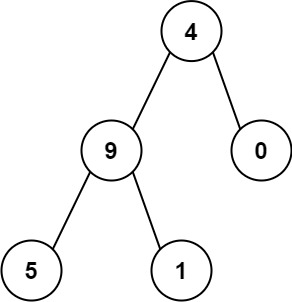
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

提示：

• 树中节点的数目在范围 [1, 1000] 内
• 0 ≤ Node.val ≤ 9
• 树的深度不超过10

思路

从根节点开始来一个左递归深度优先搜索，当遇到叶子节点后停止递归。

到了叶子节点后，使用秦九邵算法计算path的值。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        if( root == nullptr )   return 0;
        if( root->left == nullptr && root->right == nullptr )   return root->val;
        int sum = 0;
        vector<int> path;
        path.emplace_back( root->val );
        dfs(root, path, sum);
        return sum;
    }
    void dfs(TreeNode* node, vector<int>& path, int& sum) {
        // 1. Exit condition: leaf node
        if( node->left == nullptr && node->right == nullptr ) {
            sum += compute_sum(path);
            return;
        }
        // 2. Walk every node that not visited
        if( node->left != nullptr ) {
            path.emplace_back( node->left->val );
            dfs(node->left, path, sum);
            path.pop_back();
        }
        if( node->right != nullptr ) {
            path.emplace_back( node->right->val );
            dfs(node->right, path, sum);
            path.pop_back();
        }
    }
    int compute_sum(vector<int>& path) {
        int sum = 0;
        for(int i = 0; i < path.size(); i++) // QinJiuShao algorithm/Horner algorithm
            sum = sum * 10 + path[i];
        return sum;
    }
};