省份数量-547

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

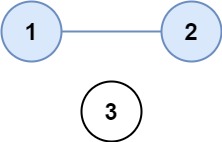
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

示例 2：

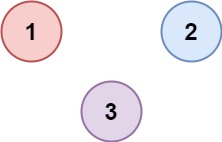
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

提示：

• 1 ≤ n ≤ 200；
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

思路

并查集（Disjoint Set）是用于判断一个图里有没有环的，对于知识点的讲解推荐正月点灯笼的视频。

题目以邻接矩阵的形式给出了图，该矩阵是方阵。我们为图创建一个并查集：

• 新建一个int parent[ isConnected.size() ]数组，长度和矩阵的边长一样；
• 为parent的每个元素赋值为自己本身，比如parent[0] = 0、parent[1] = 1；意味着该点的父节点是它自己；
• 编写find_root()方法，用于查找某个节点的父节点；
• 编写union_find()方法，用于将两个点的父子关系；
• 最后遍历一遍parent数组，当parent[i] == i时，省份数目加一；

代码

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        if( isConnected.size() == 1 )   return 1;
        // Create a parent array
        vector<int> parent( isConnected.size() );
        for(int i = 0; i < isConnected.size(); i++) {
            parent[i] = i;     // parent is itself
        }
        // Union all the nodes
        for(int i = 1; i < isConnected.size(); i++) {
            for(int j = 0; j < i; j++) {
                if( isConnected[i][j] == 1 ) {
                    union_find(i, j, parent);
                }
            }
        }
        // Walk the parent and find the provience
        unsigned counter = 0;
        for(int i = 0; i < parent.size(); i++) {
            if( parent[i] == i ) 
                counter++;
        }
        return counter;
    }
    int find_root(int node, const vector<int>& parent) {
        while( parent[node] != node ) {
            node = parent[ node ];
        }
        return node;
    }
    void union_find(int node_a, int node_b, vector<int>& parent) {
        int a_root = find_root(node_a, parent);
        int b_root = find_root(node_b, parent);
        parent[a_root] = b_root;
    }
};