一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

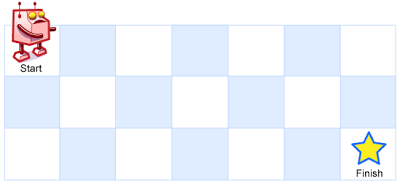
不同路径-62 - 图1

  1. Input: m = 3, n = 7
  2. Output: 28

示例 2：

  1. Input: m = 3, n = 2
  2. Output: 3
  3. Explanation:
  4. From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
  5. 1. Right -> Down -> Down
  6. 2. Down -> Down -> Right
  7. 3. Down -> Right -> Down

示例 3：

  1. Input: m = 7, n = 3
  2. Output: 28

示例 4：

  1. Input: m = 3, n = 3
  2. Output: 6

提示：

  • 1 ≤ m, n ≤ 100
  • 题目数据保证答案小于等于 2 × 10

思路

最开始尝试用DFS，但在大的测试数据下超时了。后来想想可以用动态规划。

我们创建一个二维dp[][]数组，里面的值含义是：有多少个方法来到当前坐标位置。

  • 当只有 1 行 1 列时，dp[0][0] = 1；

  • 假设有 3 行 7 列时，dp[][]数组的第0行和第0列的值全是1，因为机器人每次只能往右走或往下走：

    1. dp[3][7] = {
    2.   1, 1, 1, 1, 1, 1, 1,
    3.   1, 0, 0, 0, 0, 0, 0,
    4.   1, 0, 0, 0, 0, 0, 0
    5. }
  • 当走到 row 行 col 列时，它可能是从 上面 来的或从 左边 来的，所以到当前位置的走法有： 不同路径-62 - 图2(col)%20%3D%20%0A%5Cbegin%7Bcases%7D%0A1%2C%20%26row%20%3D%200%2C%20col%20%3D%200%5C%5C%0Adp(row-1)(col)%20%2B%20dp(row)(col-1)%2C%20%26%20row%20%5Cge%201%2C%20col%20%5Cge%201%0A%5Cend%7Bcases%7D%0A#card=math&code=dp%28row%29%28col%29%20%3D%20%0A%5Cbegin%7Bcases%7D%0A1%2C%20%26row%20%3D%200%2C%20col%20%3D%200%5C%5C%0Adp%28row-1%29%28col%29%20%2B%20dp%28row%29%28col-1%29%2C%20%26%20row%20%5Cge%201%2C%20col%20%5Cge%201%0A%5Cend%7Bcases%7D%0A)

有了状态转移方程，我们能求出各阶段dp[][]的值。结果返回dp[][]数组右下角的那个元素。

代码

  1. // 第一次尝试：37/62 超出时间限制
  2. class Solution {
  3. public:
  4.     int uniquePaths(int m, int n) {
  5.         if( m == 0 || n == 0 )   return 0;
  6.         if( n == 1 )   return 1;
  8.         bool visited[ m ][101];
  9.         for(int i = 0; i < m; i++) {
  10.             for(int j = 0; j < 101; j++) {
  11.                 visited[i][j] = false;
  12.             }
  13.         }
  15.         int metadata[3] = { m, n, 0 };
  16.         dfs(0, 0, visited, metadata);
  17.         return metadata[2];
  18.     }
  20.     void dfs(int row, int col, bool visited[][101], int metadata[]) {
  21.         // 1. Exit conditon
  22.         if( row == metadata[0] - 1 && col == metadata[1] - 1 ) {
  23.             metadata[2]++;
  24.             return;
  25.         }
  27.         // 2. Walk every node that not visited
  28.         visited[row][col] = true;
  29.         if( row+1 < metadata[0] && !visited[row+1][col] )   dfs(row + 1, col, visited, metadata);
  30.         if( col+1 < metadata[1] && !visited[row][col+1] )   dfs(row, col + 1, visited, metadata);
  31.         visited[row][col] = false;
  32.     }
  33. };

AC代码如下:

  1. class Solution {
  2. public:
  3.     int uniquePaths(int m, int n) {
  4.         if( m == 0 || n == 0 )   return 0;
  5.         if( n == 1 )   return 1;
  7.         int dp[m][n];
  8.         for(int i = 0; i < n; i++)   dp[0][i] = 1;
  9.         for(int i = 0; i < m; i++)   dp[i][0] = 1;
  11.         for(int i = 1; i < m; i++) {
  12.             for(int j = 1; j < n; j++) {
  13.                 dp[i][j] = dp[i-1][j] + dp[i][j-1];
  14.             }
  15.         }
  17.         return dp[m-1][n-1];
  18.     }
  19. };