一、题目

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

点击查看原题

二、思路

题中已叙述清楚前缀树的功能，其目的主要是可以通过给定字符串s，根据放置入数据结构中的字符串进行查询：
1）查询是否存在和字符串s一模一样的字符串
2）查询数据结构中是否存在前缀为字符串s的串
准确理解题意的基础上，对进行数据结构的构思：
1）整个数据结构为以字符为节点的树，便于做上述的第二种查询
2）由于会存在放入的多个字符串共用同一前缀的情况，可以设定一个path值，用以代表共用该字符的字符串数量，如图：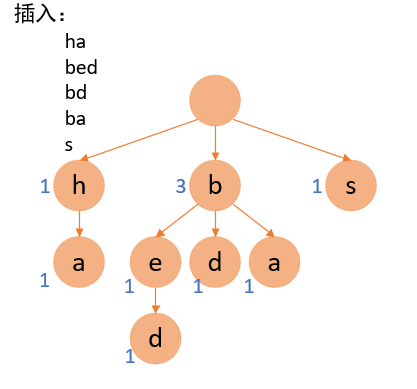

3）当数据结构如上所示时，当插入一个字符串如“b”时，那就无法区分结尾，此时可以再设计一个end值，以此代表有多少个字符串以当前字符结尾
4）每一个节点的孩子节点最多有26个，可是开辟数组进行保存会很大程度浪费空间，可以使用了Map的键值对实现孩子节点的存放（另一种实现是建立一个容量为26的数组进行实现）

三、实现

于是可以将对象初始化为：

class Trie {
    public int end;
    public int path;
    public Map<Character, Trie> next;
    /** Initialize your data structure here. */
    public Trie() {
        end = 0;
        path = 0;
        next = new HashMap<>();
    }
}

插入函数为：

public void insert(String word) {
    char[] cWords = word.toCharArray();
    Trie node = this;
    for (char cWord : cWords) {
        if (!node.next.containsKey(cWord)) {
            node.next.put(cWord, new Trie());
        }
        node = node.next.get(cWord);    // 获取孩子节点
        node.path++;    
    }
    node.end++;        // 标记该字符有字符串结尾
}

第一种搜索函数（全匹配）为：

public boolean search(String word) {
    char[] cWords = word.toCharArray();
    Trie node = this;
    for (char cWord : cWords) {
        if (!node.next.containsKey(cWord)) {    // 当不存在其中任一字符就判定不存在该字符串
            return false;
        }
        node = node.next.get(cWord);
    }
    return node.end > 0;    // 遍历到word的最后一个字符，有字符串在此结尾，就存在word
}

第二种搜索（前缀匹配）为：

public boolean startsWith(String prefix) {
    char[] cWords = prefix.toCharArray();
    Trie node = this;
    for (char cWord : cWords) {
        if (!node.next.containsKey(cWord)) {
            return false;
        }
        node = node.next.get(cWord);
    }
    return true;
}