一、题目

给你一个由 无重复 正整数组成的集合 nums ，请你找出并返回其中最大的整除子集 answer ，子集中每一元素对 (answer[i], answer[j]) 都应当满足：

  • answer[i] % answer[j] == 0 ，或
  • answer[j] % answer[i] == 0

如果存在多个有效解子集，返回其中任何一个均可。

点击查看原题

二、思路

提示：该题题意很容易被曲解，认为一定从第一个元素开始，或认为一定从最后一个元素结束，并且给出的两个可能性条件，也让人摸不着头脑。
1、拿到本题，首先想到的应该是排序，如果给出的nums是有序的，寻找有效子集，只需要往一个方向寻找即可。
2、先思考暴力法：暴力法就是把所有情况都遍历一下，大概推导一下，会发现有重复子问题。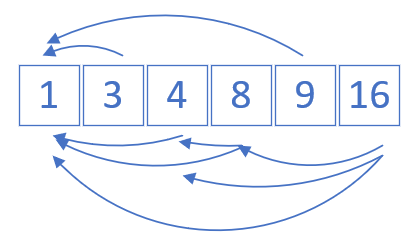
image.png
如上图，可以观察到，暴力解法会重复计算16->4->1的可能性，那就将其记录下来即可，状态转移方程为：
368. 最大整除子集-每日一题 - 图2
dp[i]记录了从nums[0]到nums[i]中，以包含nums[i]的最大整除子集长度。（这里有点绕，需好好理解）

再用一个route来记录最大整除子集的元素下标路线。

三、代码

  1. class Solution {
  2.     public List<Integer> largestDivisibleSubset(int[] nums) {
  3.         int[] dp = new int[nums.length];
  4.         int[] route = new int[nums.length];
  5.         int maxVal = 0;
  6.         int loc = 0;
  7.         Arrays.sort(nums);
  8.         for (int i = 0; i < route.length; i++) {
  9.             route[i] = -1;    // 初始化为-1，是为了防止与下标0重合
  10.         }
  11.         for (int i = 0; i < nums.length; i++) {
  12.             dp[i] = 1;    // 最小会有一个元素，那就是长度为1
  13.             for (int j = 0; nums[j] * 2L <= nums[i]; j++) {    //最多到num[i]/2，2L是防止乘法溢出
  14.                 // 判断是否能被整除
  15.                 if ((nums[i] % nums[j] == 0) && dp[j] + 1 > dp[i]) {    
  16.                     dp[i] = dp[j] + 1;
  17.                     route[i] = j;    // 记录上一个元素的下标
  18.                 }
  19.             }
  20.             if (dp[i] > maxVal) {    // 记录最大整除子集最后一个元素的位置
  21.                 maxVal = dp[i];
  22.                 loc = i;
  23.             }
  24.         }
  26.         List<Integer> ans = new ArrayList();
  28.         while (loc != -1) {        //根据route记录的路线去添加元素，从后往前
  29.             ans.add(nums[loc]);    
  30.             loc = route[loc];
  31.         }
  32.         Collections.reverse(ans);
  33.         return ans;
  34.     }
  35. }

时间复杂度为O(n^2)，空间复杂度为O(n)