一、题目

使用下面描述的算法可以扰乱字符串 s 得到字符串 t ：
如果字符串的长度为 1 ，算法停止
如果字符串的长度 > 1 ，执行下述步骤：
1）在一个随机下标处将字符串分割成两个非空的子字符串。即，如果已知字符串 s ，则可以将其分成两个子字符串 x 和 y ，且满足 s = x + y 。
2）随机决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即，在执行这一步骤之后，s 可能是 s = x + y 或者 s = y + x 。
3）在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法。
给你两个长度相等的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。如果是，返回 true ；否则，返回 false 。

点击查看题目

二、思路

此题思路大致可以理解为，将字符串拆解成树，如下图（摘自负雪明烛题解）：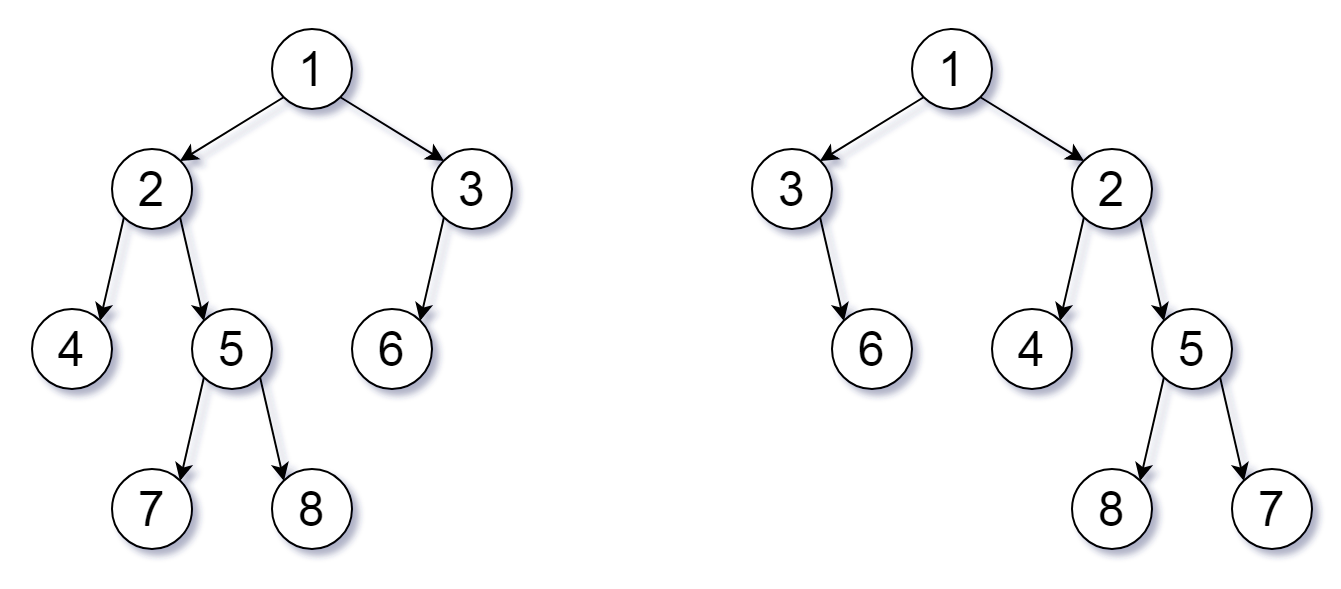
87. 扰乱字符串-每日一题 - 图1
只需要对树进行递归判断：
1）图一左子树==图二左子树，且图一右子树==图二右子树，则字符串为扰乱字符串
2）图一左子树==图二右子树，且图一右子树==图二左子树，则字符串为扰乱字符串
3）其他情况则不为扰乱字符串
理解上述核心思想，则可知大致解题思路，但所给数据为两个字符串，而非建立好的树，那么如何进行树的建立和判断？
建立：首先使用穷举的方式，每个地方都做一下切分和判断。
判断：图一左子树上的元素种类和数量，一定是等于图二的左子树或右子树的，否则肯定不可能相等。

使用一个三维数组进行记录计算过的字符串片段，避免重复计算子问题。memo数组，memo[loc1][loc2][len]指第一个字符串中[loc1，loc1+len)与[loc2，loc2+len)是否为扰乱字符串。值为1：是扰乱字符串；值为-1：不是扰乱字符串；值为0：未计算过。

三、代码

class Solution {
    private String s1;
    private String s2;
    private int[][][] memo;        // 记录的数组
    public boolean isScramble(String s1, String s2) {
        this.s1 = s1;
        this.s2 = s2;
        int len = s1.length();
        memo = new int[len][len][len+1];
        return dfs(0, 0, len);    
    }
    public boolean dfs(int loc1, int loc2, int len) {
        if (memo[loc1][loc2][len] != 0) {    // 当该两个字符串片段计算过，则返回之前的计算结果
            return memo[loc1][loc2][len] == 1;
        }
        if (s1.substring(loc1, loc1 + len).equals(s2.substring(loc2, loc2 + len))) {    // 直接判断字符串是否完全相等(即字符串中字符顺序一模一样)
            memo[loc1][loc2][len] = 1;
            return true;
        }
        if (!check(loc1, loc2, len)) {    // 如果元素数量种类都不相同，则肯定不是扰乱字符串
            memo[loc1][loc2][len] = -1;
            return false;
        }
        for (int i = 1; i < len; i++) {
            if (dfs(loc1, loc2, i) && dfs(loc1+i, loc2+i, len-i)) {        // 左右子树没有交换，即判断问题：图一左子树==图二左子树，且图一右子树==图二右子树
                memo[loc1][loc2][len] = 1;
                return true;
            }
            if (dfs(loc1, loc2+len-i, i) && dfs(loc1+i, loc2, len-i)) {    // 左右子树交换，即判断问题：图一左子树==图二右子树，且图一右子树==图二左子树
                memo[loc1][loc2][len] = 1;
                return true;
            }
        }
        memo[loc1][loc2][len] = -1;
        return false;
    }
    public boolean check(int loc1, int loc2, int len) {
        int[] re = new int[26];
        for (int i = loc1; i < loc1 + len; i++) {    // 第一个字符串的所有字母数量，记录在到数组中，为正值
            re[s1.charAt(i) - 'a']++;
        }
        for (int i = loc2; i < loc2 + len; i++) {    // 第二个字符串的所有字母数量，记录在到数组中，为负值
            re[s2.charAt(i) - 'a']--;
        }
        for (int i = 0; i < 26; i++) {    // 如果上面两次统计后，所有空位都抵消为0，则字串字符种类和数量完全一致
            if (re[i] != 0) {
                return false;
            }
        }
        return true;
    }
}

其实，在dfs函数中的for循环中，是穷举切分点，每次都需要重新统计，也属于重复计算了子问题，可以再次进行优化：即切分点的位置，一定是字符种类数量相等的两个片段。
其他部分不变，dfs函数部分改动如下（由于字符串规模较小，无法体现该算法优势）：

public boolean dfs(int loc1, int loc2, int len) {
        if (memo[loc1][loc2][len] != 0) {    // 当该两个字符串片段计算过，则返回之前的计算结果
            return memo[loc1][loc2][len] == 1;
        }
        if (s1.substring(loc1, loc1 + len).equals(s2.substring(loc2, loc2 + len))) {    // 直接判断字符串是否完全相等(即字符串中字符顺序一模一样)
            memo[loc1][loc2][len] = 1;
            return true;
        }
        if (!check(loc1, loc2, len)) {    // 如果元素数量种类都不相同，则肯定不是扰乱字符串
            memo[loc1][loc2][len] = -1;
            return false;
        }
    // ----------------------------改动如下--------------------------------------
        int[] re = new int[26];
        int sum = 0;
        for (int i = 0; i < len-1; i++) {
            int t1 = s1.charAt(loc1+i) - 'a', t2 = s2.charAt(loc2+i) - 'a';
            re[t1]++;
            if (re[t1] > 0) {    // 使用一个计数的技巧，当sum为0的时候，一定是re数组每个记录都为0的时候，这部分不展开，感兴趣可以自行推导
                sum++;
            }
            re[t2]--;
            if (re[t2] >= 0) {
                sum--;
            }
            if (sum == 0) {
                if (dfs(loc1, loc2, i+1) && dfs(loc1+i+1, loc2+i+1, len-i-1)) {        // 左右子树没有交换，即判断问题：图一左子树==图二左子树，且图一右子树==图二右子树
                    memo[loc1][loc2][len] = 1;
                    return true;
                }
            }
        }
        re = new int[26];
        sum = 0;
        for (int i = 0; i < len-1; i++) {
            int t1 = s1.charAt(loc1+i) - 'a', t2 = s2.charAt(loc2 + len-i-1) - 'a';
            re[t1]++;
            if (re[t1] > 0) {
                sum++;
            }
            re[t2]--;
            if (re[t2] >= 0) {
                sum--;
            }
            if (sum == 0) {
                if (dfs(loc1, loc2+len-i-1, i+1) && dfs(loc1+i+1, loc2, len-i-1)) {        // 左右子树没有交换，即判断问题：图一左子树==图二左子树，且图一右子树==图二右子树
                    memo[loc1][loc2][len] = 1;
                    return true;
                }
            }
        }
    // ----------------------------end--------------------------------------
        memo[loc1][loc2][len] = -1;
        return false;
    }