时序Python
在处理数据的时候，经常会遇到一些非连续的散点时间序列数据：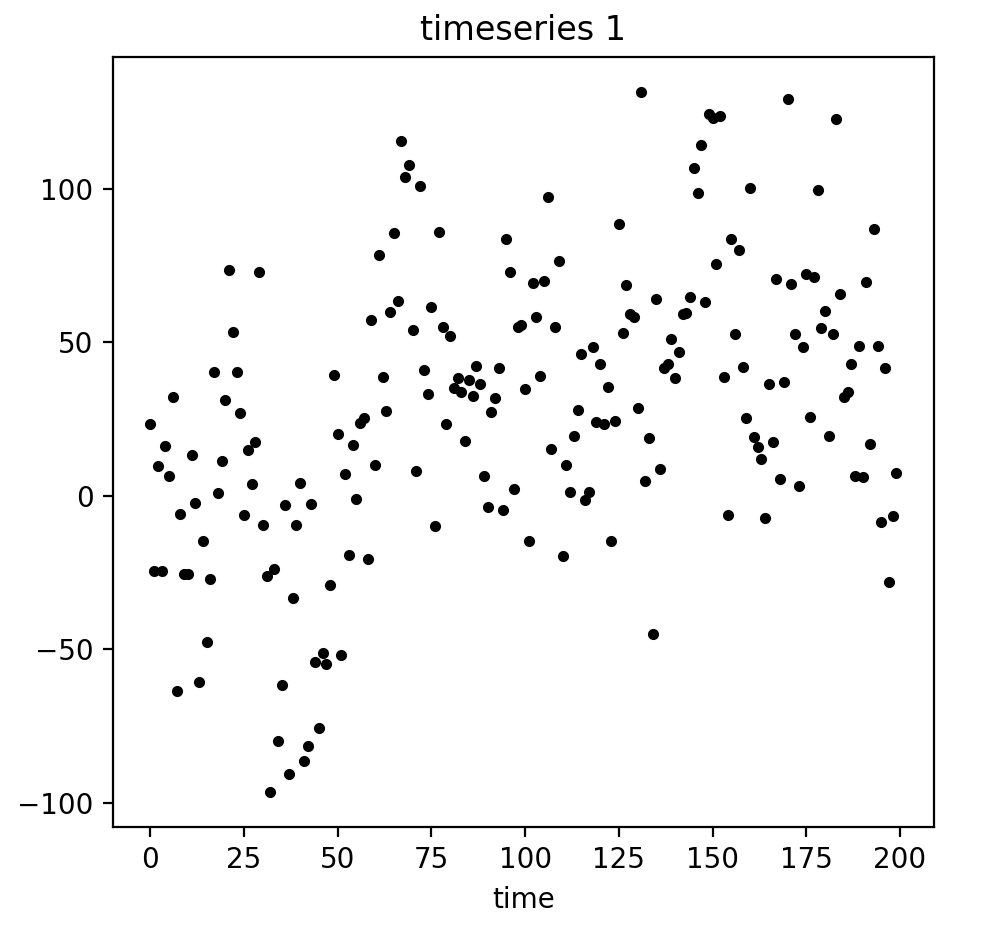

有些时候，这样的散点数据是不利于进行数据的聚类和预测的。因此需要把它们平滑化，如下图所示：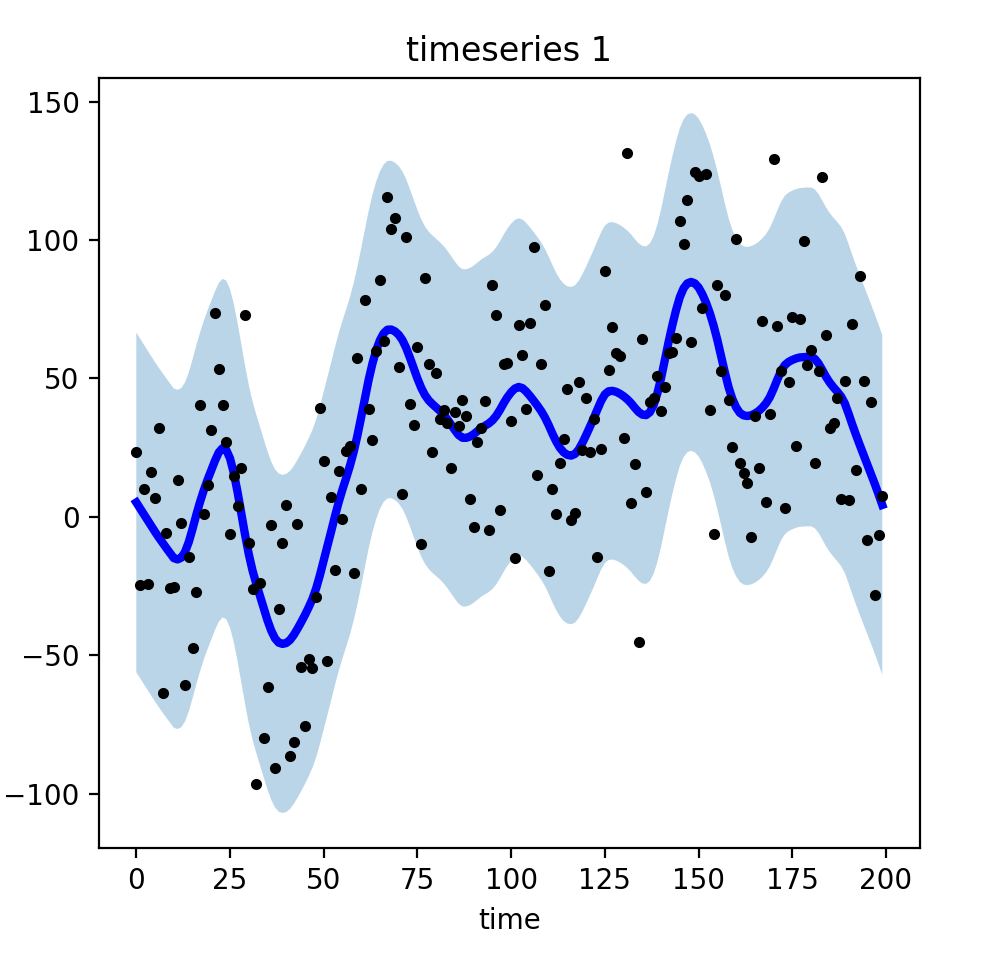

如果将散点及其范围区间都去除，平滑后的效果如下：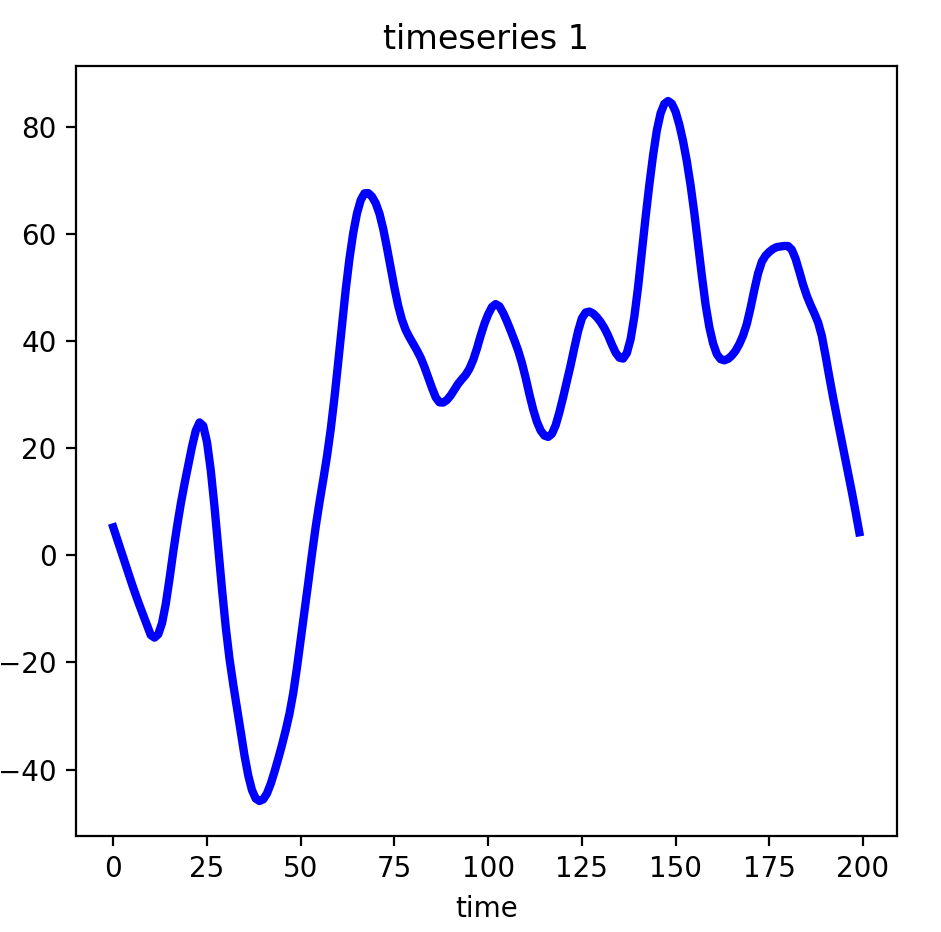

这样的时序数据是不是看起来舒服多了？此外，使用平滑后的时序数据去做聚类或预测或许有令人惊艳的效果，因为它去除了一些偏差值并细化了数据的分布范围。
如果自己开发一个这样的平滑工具，会耗费不少的时间。因为平滑的技术有很多种，需要一个个地去研究，找到最合适的技术并编写代码，这是一个非常耗时的过程。平滑技术包括但不限于：

• 指数平滑
• 具有各种窗口类型（常数、汉宁、汉明、巴特利特、布莱克曼）的卷积平滑
• 傅立叶变换的频谱平滑
• 多项式平滑
• 各种样条平滑（线性、三次、自然三次）
• 高斯平滑
• 二进制平滑

所幸，有大佬已经实现好了时间序列的这些平滑技术，并在GitHub上开源了这份模块的代码——它就是 Tsmoothie 模块。

1、准备

开始之前，要确保Python和pip已经成功安装在电脑上。
请选择以下任一种方式输入命令安装依赖：

1. Windows 环境 打开 Cmd (开始-运行-CMD)。
2. MacOS 环境 打开 Terminal (command+空格输入Terminal)。
3. 如果用的是 VSCode编辑器 或 Pycharm，可以直接使用界面下方的Terminal。

   pip install tsmoothie

   (PS) Tsmoothie 仅支持Python 3.6 及以上的版本。

   2、Tsmoothie 基本使用

   为了尝试Tsmoothie的效果，需要生成随机数据： ```python import numpy as np import matplotlib.pyplot as plt from tsmoothie.utils_func import sim_randomwalk from tsmoothie.smoother import LowessSmoother

生成 3 个长度为200的随机数据组

np.random.seed(123) data = sim_randomwalk(n_series=3, timesteps=200, process_noise=10, measure_noise=30)

然后使用Tsmoothie执行平滑化：
```python
# 平滑
smoother = LowessSmoother(smooth_fraction=0.1, iterations=1)
smoother.smooth(data)

通过 smoother.smooth_data 就可以获取平滑后的数据：

print(smoother.smooth_data)
# [[ 5.21462928 3.07898076 0.93933646 -1.19847767 -3.32294934
# -5.40678762 -7.42425709 -9.36150892 -11.23591897 -13.05271523
# ....... ....... ....... ....... ....... ]]

绘制效果图：

# 生成范围区间
low, up = smoother.get_intervals('prediction_interval')
plt.figure(figsize=(18,5))
for i in range(3):
    plt.subplot(1,3,i+1)
    plt.plot(smoother.smooth_data[i], linewidth=3, color='blue')
    plt.plot(smoother.data[i], '.k')
    plt.title(f"timeseries {i+1}"); plt.xlabel('time')
    plt.fill_between(range(len(smoother.data[i])), low[i], up[i], alpha=0.3)

3、基于Tsmoothie的极端异常值检测

事实上，基于smoother生成的范围区域，可以进行异常值的检测：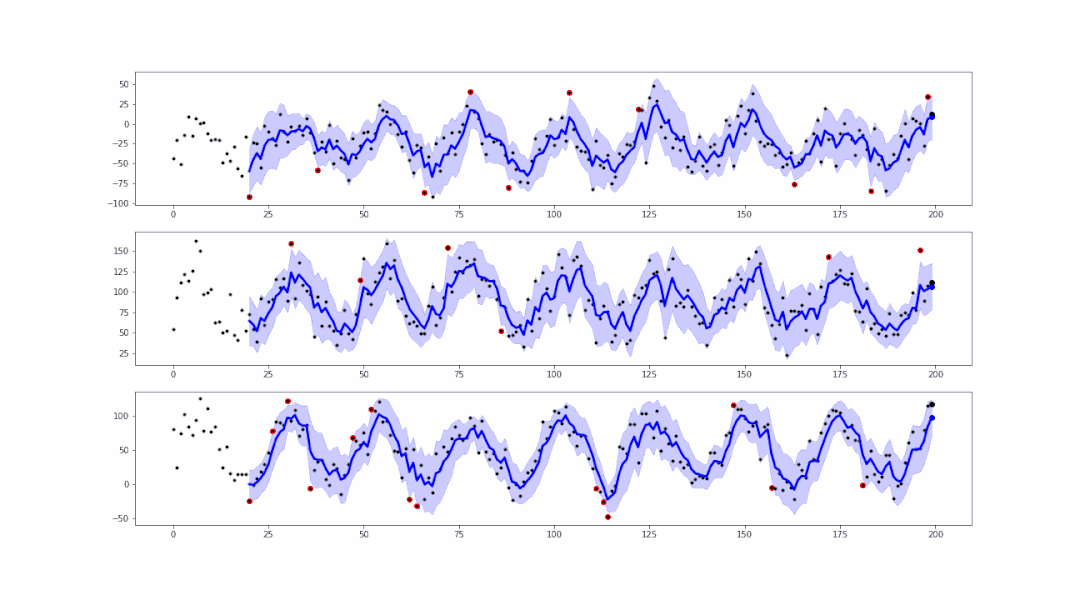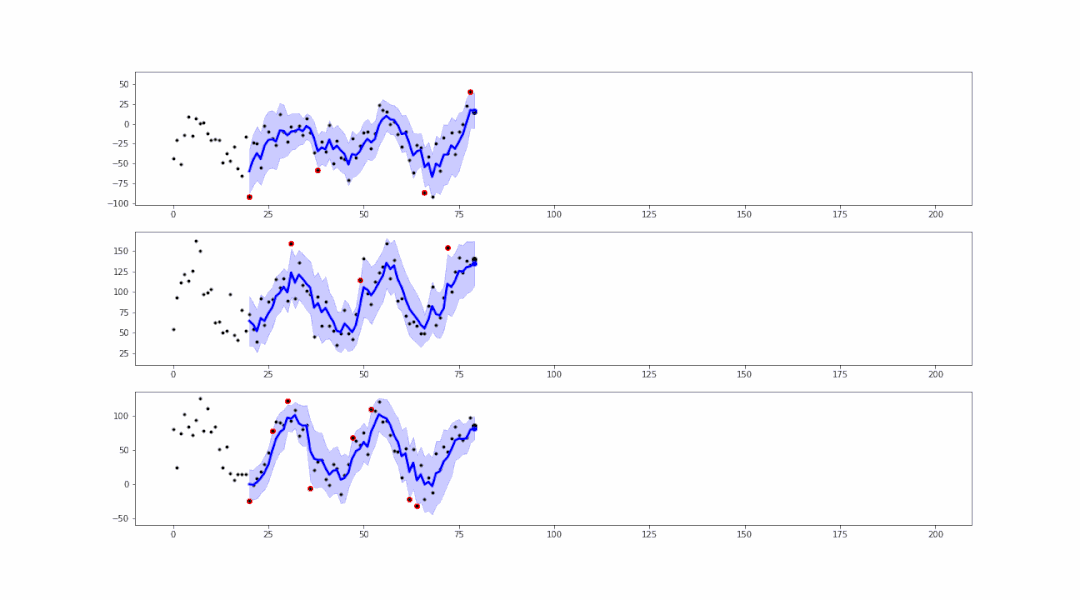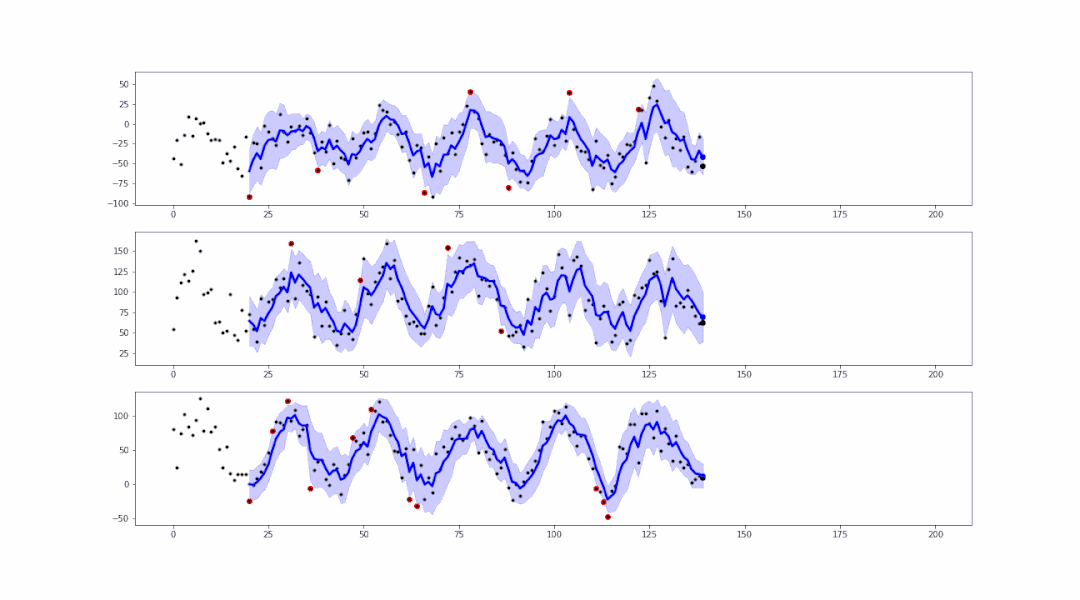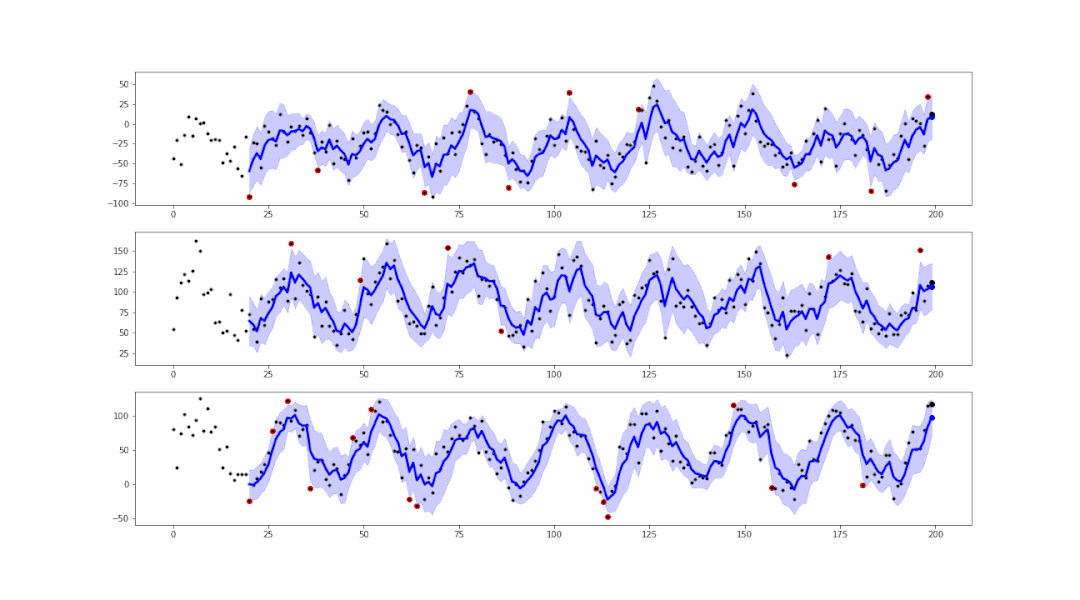

可以看到，在蓝色范围以外的点，都属于异常值。可以轻易地将这些异常值标红或记录，以便后续的处理。

_low, _up = smoother.get_intervals('sigma_interval', n_sigma=2)
series['low'] = np.hstack([series['low'], _low[:,[-1]]])
series['up'] = np.hstack([series['up'], _up[:,[-1]]])
is_anomaly = np.logical_or(
    series['original'][:,-1] > series['up'][:,-1],
    series['original'][:,-1] < series['low'][:,-1]
).reshape(-1,1)

假设蓝色范围interval的最大值为up、最小值为low，如果存在 data > up 或 data < low 则表明此数据是异常点。
使用以下代码通过滚动数据点进行平滑化和异常检测，就能保存得到上方的GIF动图。

# Origin: https://github.com/cerlymarco/MEDIUM_NoteBook/blob/master/Anomaly_Detection_RealTime/Anomaly_Detection_RealTime.ipynb
import numpy as np
import matplotlib.pyplot as plt
from celluloid import Camera
from collections import defaultdict
from functools import partial
from tqdm import tqdm
from tsmoothie.utils_func import sim_randomwalk, sim_seasonal_data
from tsmoothie.smoother import *
def plot_history(ax, i, is_anomaly, window_len, color='blue', **pltargs):
    posrange = np.arange(0,i)
    ax.fill_between(posrange[window_len:],
                    pltargs['low'][1:], pltargs['up'][1:],
                    color=color, alpha=0.2)
    if is_anomaly:
        ax.scatter(i-1, pltargs['original'][-1], c='red')
    else:
        ax.scatter(i-1, pltargs['original'][-1], c='black')
    ax.scatter(i-1, pltargs['smooth'][-1], c=color)
    ax.plot(posrange, pltargs['original'][1:], '.k')
    ax.plot(posrange[window_len:],
            pltargs['smooth'][1:], color=color, linewidth=3)
    if 'ano_id' in pltargs.keys():
        if pltargs['ano_id'].sum()>0:
            not_zeros = pltargs['ano_id'][pltargs['ano_id']!=0] -1
            ax.scatter(not_zeros, pltargs['original'][1:][not_zeros],
                       c='red', alpha=1.)
np.random.seed(42)
n_series, timesteps = 3, 200
data = sim_randomwalk(n_series=n_series, timesteps=timesteps,
                      process_noise=10, measure_noise=30)
window_len = 20
fig = plt.figure(figsize=(18,10))
camera = Camera(fig)
axes = [plt.subplot(n_series,1,ax+1) for ax in range(n_series)]
series = defaultdict(partial(np.ndarray, shape=(n_series,1), dtype='float32'))
for i in tqdm(range(timesteps+1), total=(timesteps+1)):
    if i>window_len:
        smoother = ConvolutionSmoother(window_len=window_len, window_type='ones')
        smoother.smooth(series['original'][:,-window_len:])
        series['smooth'] = np.hstack([series['smooth'], smoother.smooth_data[:,[-1]]])
        _low, _up = smoother.get_intervals('sigma_interval', n_sigma=2)
        series['low'] = np.hstack([series['low'], _low[:,[-1]]])
        series['up'] = np.hstack([series['up'], _up[:,[-1]]])
        is_anomaly = np.logical_or(
            series['original'][:,-1] > series['up'][:,-1],
            series['original'][:,-1] < series['low'][:,-1]
        ).reshape(-1,1)
        if is_anomaly.any():
            series['ano_id'] = np.hstack([series['ano_id'], is_anomaly*i]).astype(int)
        for s in range(n_series):
            pltargs = {k:v[s,:] for k,v in series.items()}
            plot_history(axes[s], i, is_anomaly[s], window_len,
                         **pltargs)
        camera.snap()
    if i>=timesteps:
        continue
    series['original'] = np.hstack([series['original'], data[:,[i]]])
print('CREATING GIF...') # it may take a few seconds
camera._photos = [camera._photos[-1]] + camera._photos
animation = camera.animate()
animation.save('animation1.gif', codec="gif", writer='imagemagick')
plt.close(fig)
print('DONE')

注意，异常点并非都是负面作用，在不同的应用场景下，它们可能代表了不同的意义。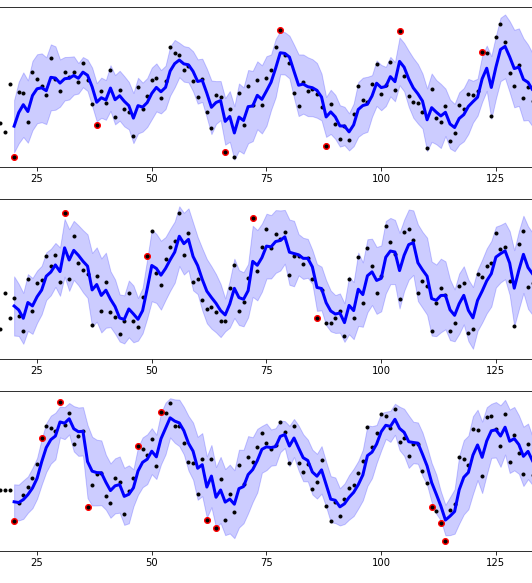

比如在股票中，它或许可以代表着震荡行情中某种趋势反转的信号。
或者在家庭用电量分析中，它可能代表着某个时刻的用电峰值，根据这个峰值可以此时此刻开启了什么样的电器。
所以异常点的作用需要根据不同应用场景进行不同的分析，才能找到它真正的价值。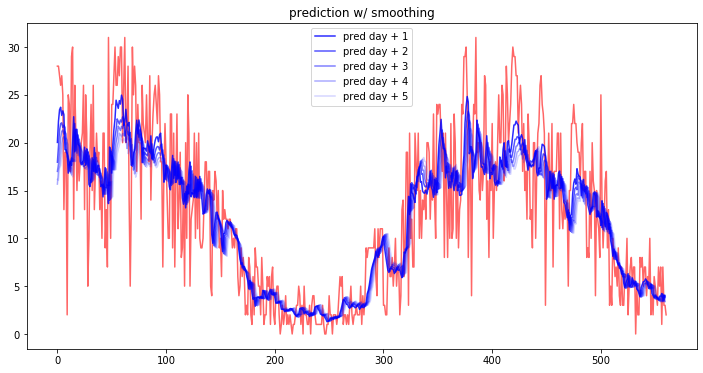

总而言之，Tsmoothie 不仅可以使用多种平滑技术平滑化时序数据，让模型训练更加有效，还可以根据平滑结果找出数据中的离群点，是做数据分析和研究的一个好帮手，非常有价值。