时间序列 自相关 偏自相关

1、简介

自相关和偏自相关的图在时序分析中有广泛的应用。
这些图以图形化的方式总结了时间序列中的一个观测值与之前的时间步长的关系强度。
两者的区别对于初学者来说是困难的以及难以理解的。
数据准备：
时序.zip
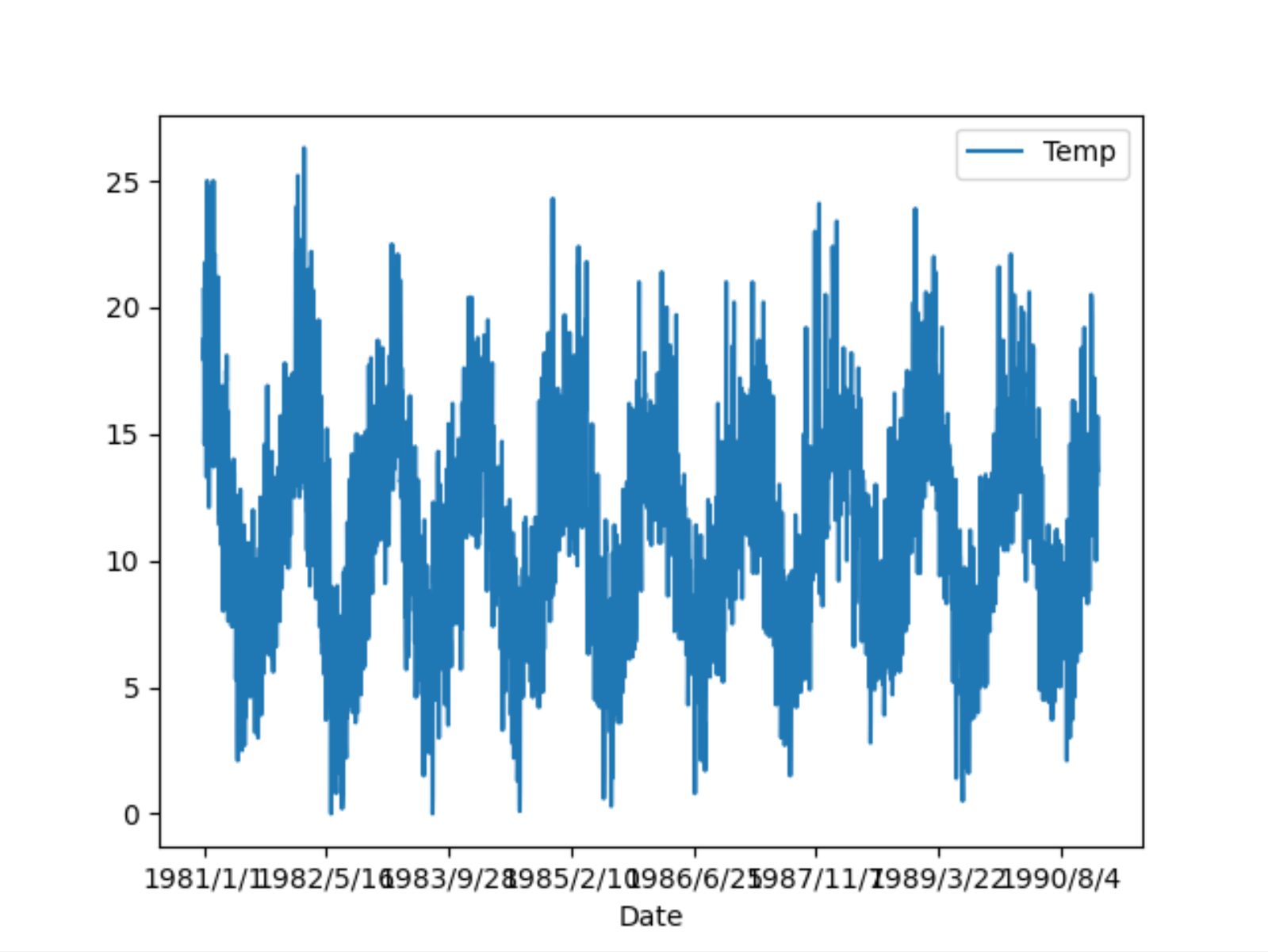
该数据集描述了澳大利亚墨尔本市10年(1981-1990年)的最低日温度。单位是摄氏度，有3650个观测值。数据的来源被认为是澳大利亚气象局。
下载数据集并将其放在当前工作目录中，文件名为“daily-minimum-temperatures.csv”。

  1. from pandas import read_csv
  2. from matplotlib import pyplot
  3. series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)
  4. series.plot()
  5. pyplot.show()

image.png
若每个变量都符合高斯分布（bell curve），则可以用 Pearson’s 相关性系数计算变量间的相关性。
计算时间序列观测值与 前一个时间步长（称为滞后（lag）） 的相关关系。
由于时间序列观测值的相关性是用同一序列的前几次值来计算的，所以这称为序列相关性或自相关性。

1.1 自相关

由滞后引起的时间序列的自相关图称为自相关函数，或简称为 ACF（ Auto Correlation Function）。这种图有时被称为相关图（correlogram）或自相关图（autocorrelation plot）。
下面是使用 statsmodels 库中的 plot_acf() 函数计算和绘制每日最低温度的自相关图的一个示例。

  1. from matplotlib import pyplot
  2. from statsmodels.graphics.tsaplots import plot_acf
  3. series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)
  4. plot_acf(series)
  5. pyplot.show()

运行该示例将创建一个2D图，x 轴上显示滞后值、y轴显示相关性 -1 和 1。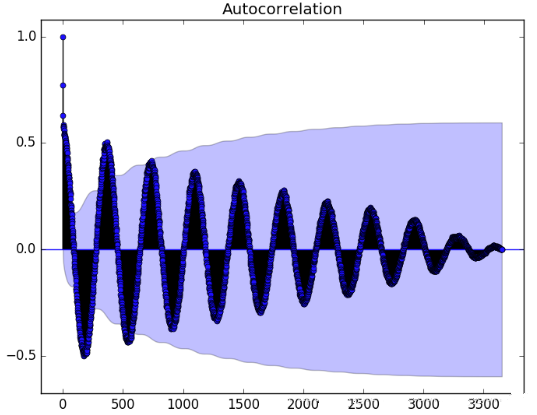
2021-08-03-08-43-38-655586.png
置信区间被画成一个圆锥体。默认情况下，这个值被设置为95%的置信区间。
默认情况下，所有的滞后值都会被打印出来，这使得绘图变得很混乱。
可以限制x轴上的滞后次数为50，以使图更容易阅读。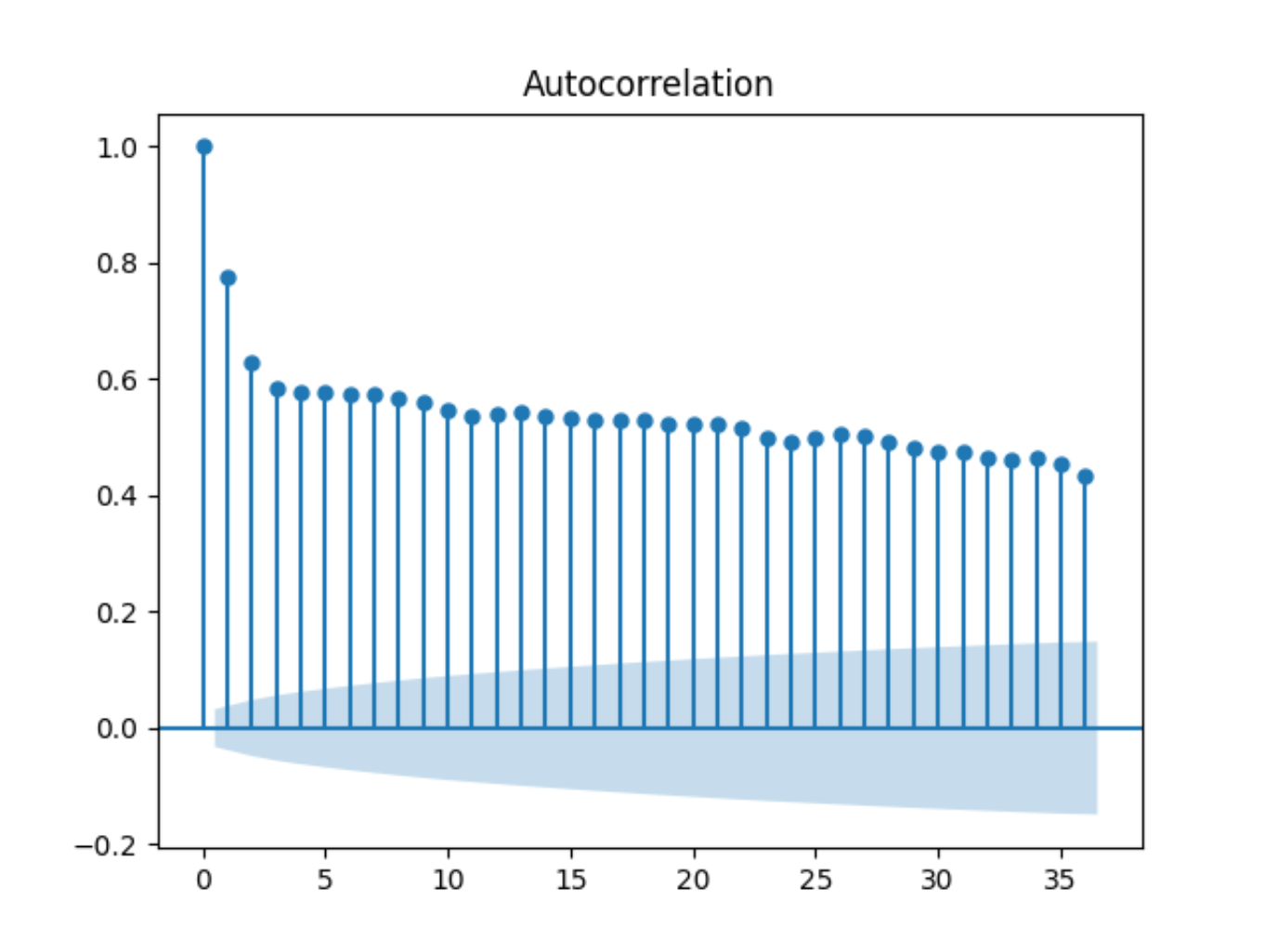
image.png

1.2 偏自相关

偏自相关是时间序列中的一个观测值与先前的观测值之间的关系的总结，其间的观测值之间的关系被删除了。
The partial autocorrelation at lag k is the correlation that results after removing the effect of any correlations due to the terms at shorter lags.
观测值与前一个时间节点的观测值的自相关由直接相关和间接相关两部分组成。间接相关是观测值的线性函数，包含时间间隔内的观测值。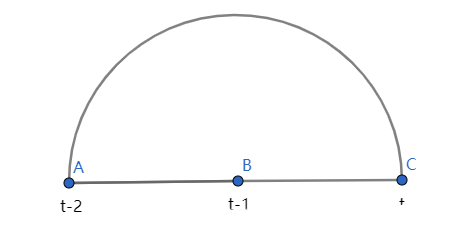
2021-08-03-08-43-38-882584.png
如上图所示，想要得到 t 节点的预测值，有两条路径：

  • 直接相关：直接由 t-2 节点得到 t
  • 间接相关：由 t-2 节点得到 t-1 节点，再由 t-1 节点得到 t 节点，偏相关用的就是间接相关

间接相关是用线性表示，如：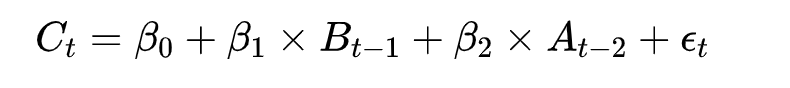
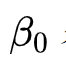image.png
image.png表示今天的相关系数，为 1。
下面的示例使用 statsmodels 库中的 plot_pacf() 来计算和绘制最小日温度数据集中前50个滞后的偏自相关函数。

  1. from pandas import read_csv
  2. from matplotlib import pyplot
  3. from statsmodels.graphics.tsaplots import plot_pacf
  4. series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)
  5. plot_pacf(series, lags=50)
  6. pyplot.show()

image.png

2、Python3 实现

  1. import numpy as np
  3. temps = np.array([68.2, 65.7, 80, 90])
  4. # ---------------------------------------------
  5. # 计算自相关,表达的是今天的数据与昨天的数据的关系强弱
  6. autocorrleation = []
  7. for shift in range(3):
  8.     if shift == 0:
  9.         corr = np.corrcoef(temps, temps)[0, 1]
  10.     else:
  11.         corr = np.corrcoef(temps[:-shift], temps[shift:])[0, 1]
  12.     autocorrleation.append(corr)
  13. # ---------------------------------------------
  14. # 计算偏自相关（partial autocorrleation)
  15. # 将数据看做残差
  16. pac = []
  17. residuals = temps  # the residuals haven't been fit yet
  19. for shift in range(3):
  20.     if shift == 0:
  21.         corr = np.corrcoef(temps, temps)[0, 1]
  22.         pac.append(corr)
  23.     else:
  24.         corr = np.corrcoef(temps[:-shift], residuals[shift:])[0, 1]
  25.         pac.append(corr)
  26.         # fit the new day's data and find the residuals
  27.         slope, intercept = np.polyfit(temps[:-shift], residuals[shift:], 1)
  28.         estimate = intercept + slope * temps[:-shift]
  29.         # update residuals
  30.         residuals[shift:] = residuals[shift:] - estimate

3、解释

3.1 自回归

自回归是与自身进行比较，提供相似性或者自身的重复。
对于滞后为 k 的自回归（autoregression，AR），ACF 描述了一个观测值和另一个观测值在前一个时间步上的自相关关系，包括直接相关和间接相关信息。
这意味着希望 AR(k) 时间序列的 ACF 在 k 的滞后上是强的，并且这种关系的惯性将持续到随后的滞后值，并在某一时刻随着影响的减弱而减弱。
PACF 只描述了观测值与其滞后之间的直接关系。这意味着 k 以外的滞后值没有相关性。

3.2 移动平均

对于滞后为 k 的移动平均（moving average，MA），其过程是一个基于前面预测值的时间序列残差自回归模型。
另一种考虑移动平均模型的方法是，它根据最近预测的误差修正未来预测。
希望 MA(k) 过程的 ACF 与最近的值有很强的相关性，直到 k 的滞后，然后急剧下降到低相关性或无相关性。
希望 PACF 图中显示出与滞后的强烈关系以及从滞后开始的相关性的减弱。