数据分析 - Scipy 与数据统计分析基础 - 《AI》

准备
统计分析
初等概率论预测结果
- 蒙特卡罗方法
随机变量和概率分布
统计假设检验
scipy.stats中的假设检验
- Shapiro-Wilk 检验
Shapiro-Wilk Test
- 安德森-达令检验
  - 做出决策
D’Agostino’s K^2 Test
- F-检验
  - 做出决策
F-test
- 皮尔逊相关系数
  - 适用范围
  - 做出决策
皮尔逊相关系数
- 斯皮尔曼等级相关
  - 做出决策
斯皮尔曼等级相关
- 肯德尔等级相关
  - 做出决策
肯德尔等级相关
- 卡方检验
  - 统计量决策
  - p值决策
scipy.stats中其他假设检验
- Box-Cox Power Transformation
  - 折线图
  - 直方图

数据分析

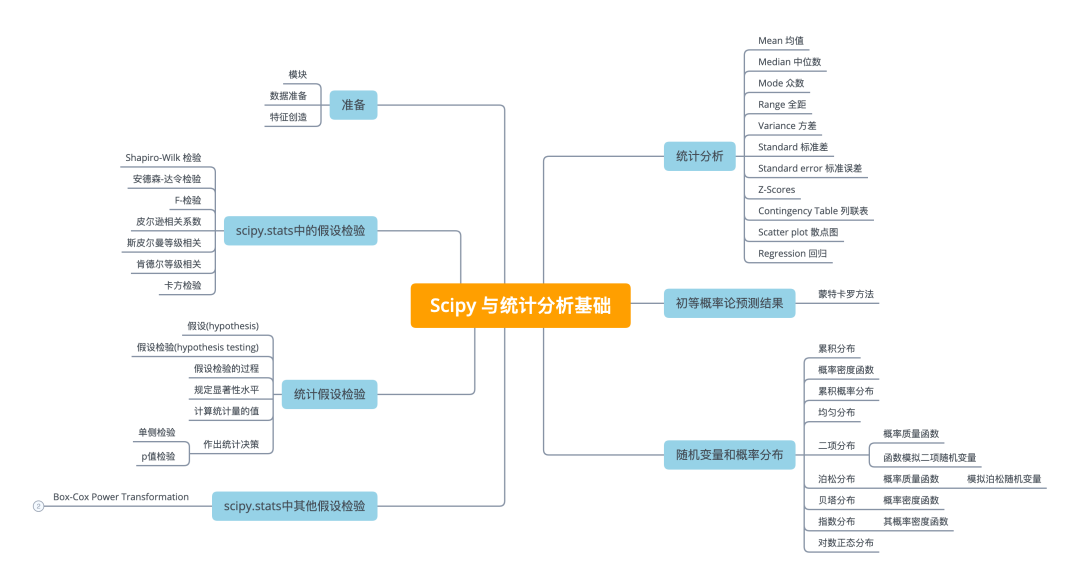
准备

统计学是一门收集、处理、分析、解释数据并从中得出结论的科学，其核心是数据。
数据分析的四个步骤，收集数据→处理数据→分析数据→解释数据。
统计学分析数据的方法有两类：

描述性分析方法总体规模、对比关系、集中趋势、离散程度、偏态、峰态、……
推断性分析方法估计、假设检验、列联分析、方差分析、相关分析、回归分析、……

模块
本文主要基于SciPy实现统计分布及检验，SciPy是基于NumPy的，提供了更多的科学计算功能，比如线性代数、优化、积分、插值、信号处理等。
Scipy包含的功能有最优化、线性代数、积分、插值、拟合、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算，而这些功能都是在之后进行数据分析需要的。
```
import seaborn as sns  
from scipy import stats  
from scipy.stats import norm  
import math
```
数据准备
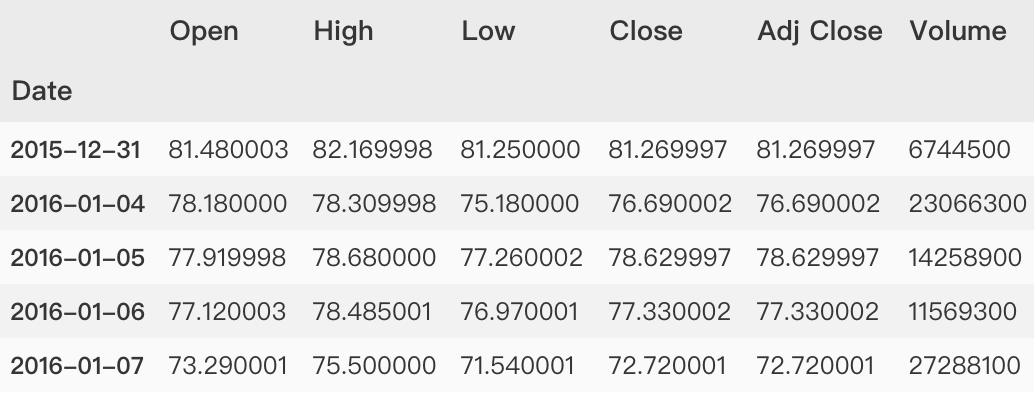
使用金融股市数据，market = ‘TCEHY’及symbol = ‘BABA’股市数据。数据样例如下所示。

特征创造
协方差矩阵(Covariance matrix)

由数据集中两两变量的协方差组成。矩阵的第个元素是数据集中第和第个元素的协方差。

协方差(Covariance)

是度量两个变量的变动的同步程度，也就是度量两个变量线性相关性程度。如果两个变量的协方差为0，则统计学上认为二者线性无关。注意两个无关的变量并非完全独立，只是没有线性相关性而已。

new_df = pd.DataFrame(
          {symbol : df['Adj Close'], 
           market : dfm['Adj Close']}, 
          index=df.index)
# 计算回报率
new_df[['stock_returns',
        'market_returns']] = new_df[[symbol,market]] / new_df[[symbol,market]].shift(1) -1
new_df = new_df.dropna()
# np.cov()对给定的数据和权重，估计协方差矩阵
# 协方差用于衡量两个变量的总体误差
covmat = np.cov(new_df["stock_returns"],
                new_df["market_returns"])
# 计算
beta = covmat[0,1]/covmat[1,1]
alpha= np.mean(new_df["stock_returns"]
              )-beta*np.mean(new_df["market_returns"])

为方便理解以上计算，打印一些结果看看。

>>> print(covmat)
[[0.00044348 0.00027564]
[0.00027564 0.00042031]]'
>>> print('Beta:', beta)
Beta: 0.6558020316481588'
>>> print('Alpha:', alpha)
Alpha: 0.00023645436856520742'

统计分析

以字段’Adj Close’为例

close = df['Adj Close']

Mean 均值

表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。

np.mean(close)
163.4495238561479

Median 中位数

按顺序排列的一组数据中居于中间位置的数。

np.median(close)
# 172.54000091552734

Mode 众数

指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。

mode = stats.mode(close)
print("中位数是 {} 计数为 {}".format(mode.mode[0], mode.count[0]))
# 中位数是 67.02999877929688 计数为 2

Range 全距

全距也叫”极差”。它是一组数据中最大值与最小值之差。可以用于度量数据的分散程度。

np.ptp(close)
# 256.5700149536133

Variance 方差

在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。

np.var(close)
# 3185.8517317644914

Standard 标准差

方差的平方根，用于度量数据如何分散程度。

np.std(close)
# 56.443349756764896

Standard error 标准误差

标准差是方差的算术平方根，估计样本均值之间的可变性。标准差能反映一个数据集的离散程度。平均数相同的，标准差未必相同。

stats.sem(close)
# 1.5907426123008535

Z-Scores

将观察值减去该组观察值的平均值，再除以标准差得到的，表示元素离均值有多少个标准差远。

znp.abs(stats.zscore(close))

[1.45596474 1.53710795 1.50273729 ... 
  1.2899743  1.32771134 1.22743374]

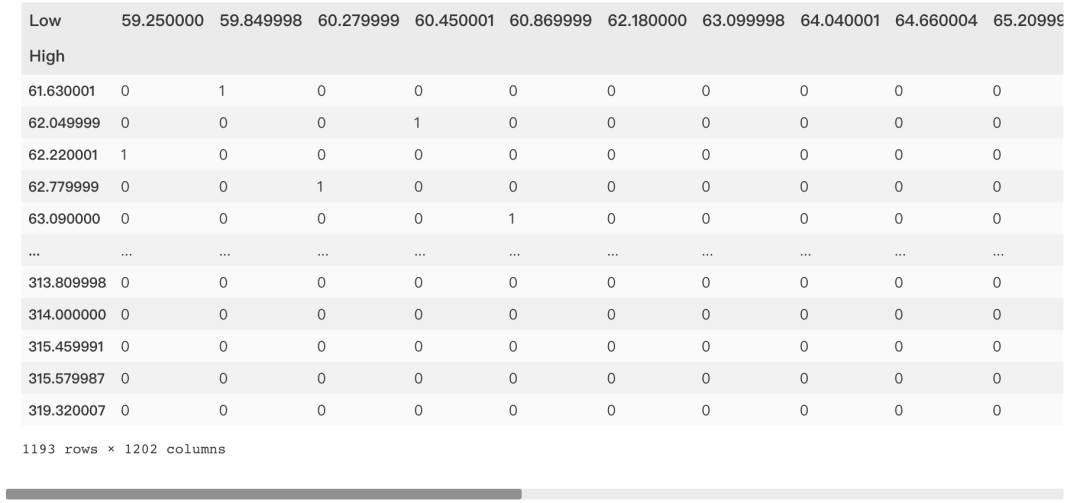
Contingency Table 列联表

列联表显示了两个变量之间的相关性。

pd.crosstab(df['High'], 
            df['Low'],  
            margins = False)

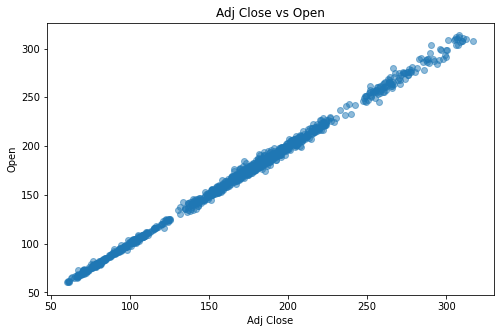
Scatter plot 散点图

散点图是指在回归分析中，数据点在直角坐标系平面上的分布图，散点图表示因变量随自变量而变化的大致趋势，据此可以选择合适的函数对数据点进行拟合。

plt.scatter(df['Adj Close'], 
            df['Open'], alpha=0.5)

Regression 回归

回归，指研究一组随机变量()和另一组()变量之间关系的统计分析方法，又称多重回归分析。是衡量一个变量的平均值与其他变量对应值之间的关系。

from sklearn.linear_model import LinearRegression
X = np.array(df['Open']).reshape(df.shape[0],-1)
y = np.array(df['Adj Close'])
LR = LinearRegression().fit(X, y)  
# 一些属性
LR.score(X, y)
LR.coef_
LR.intercept_
LR.predict(X)

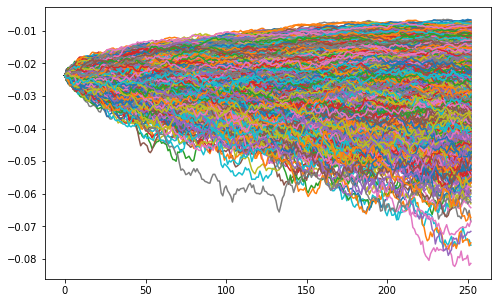
初等概率论预测结果

蒙特卡罗方法

是一种基于重复随机样本的实验计算算法。

df['Returns'] = df['Adj Close'].pct_change()
df['Returns'] = df['Returns'].dropna()
df = df.dropna()
S = df['Returns'][-1]     # 股票初始价格
T = 252                   # 交易天数
mu = df['Returns'].mean() # 均值
sigma = df['Returns'].std()*math.sqrt(252) #波幅

随机变量和概率分布

常见的股票概率分布方法

累积分布

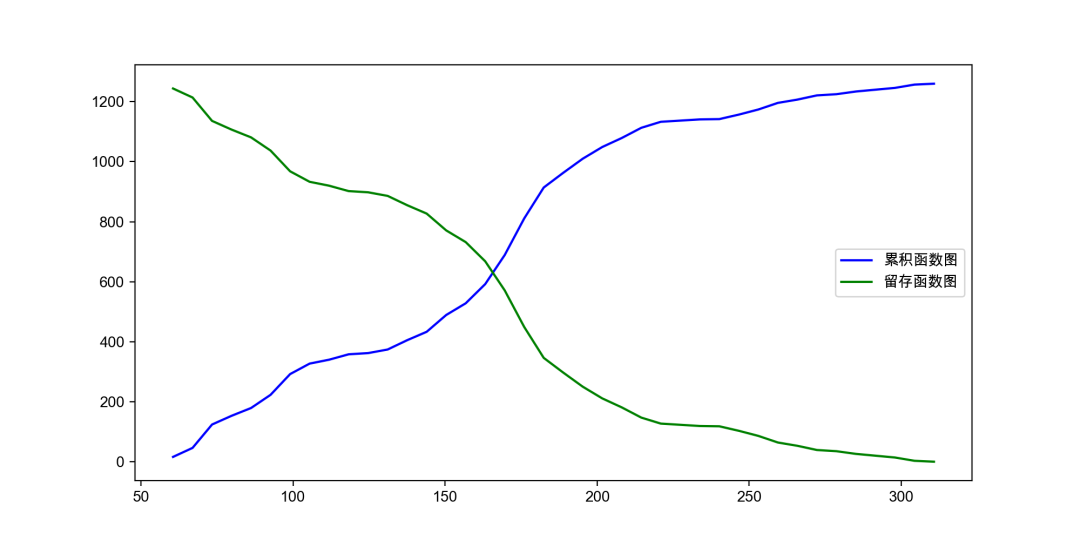
累积分布函数，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。一般以大写”CDF”（Cumulative Distribution Function）标记。
累积分布图（distribution diagram）是在一组依大小顺序排列的测量值中，当按一定的组即分组时出现测量值小于某个数值的频数或额率对组限的分布图。
在matplotlib中有两种绘图方式

plt.plot()
plt.step()

概率密度函数

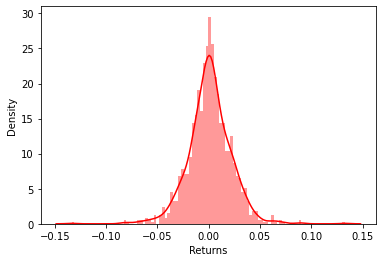
概率密度函数(Probability Density Function , PDF)是一个连续的随机变量，具有在样本空间中给定样本的值，可以解释为提供了随机变量值与该样本值相等的相对可能性。

values = df['Returns'][1:]
x = np.linspace(values.min(), values.max(), len(values))
loc, scale = stats.norm.fit(values)
param_density = stats.norm.pdf(x, loc=loc, scale=scale)
ax.hist(values, bins=30, density=True)
ax.plot(x, param_density, 'r-', label=label)

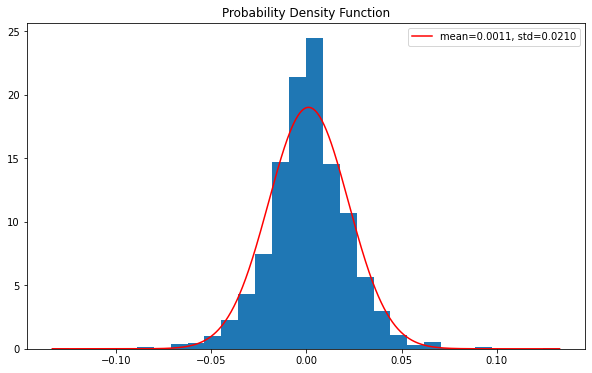
# 在这个阶段，回报率有升有降
df['Returns'].plot(figsize=(20, 8))

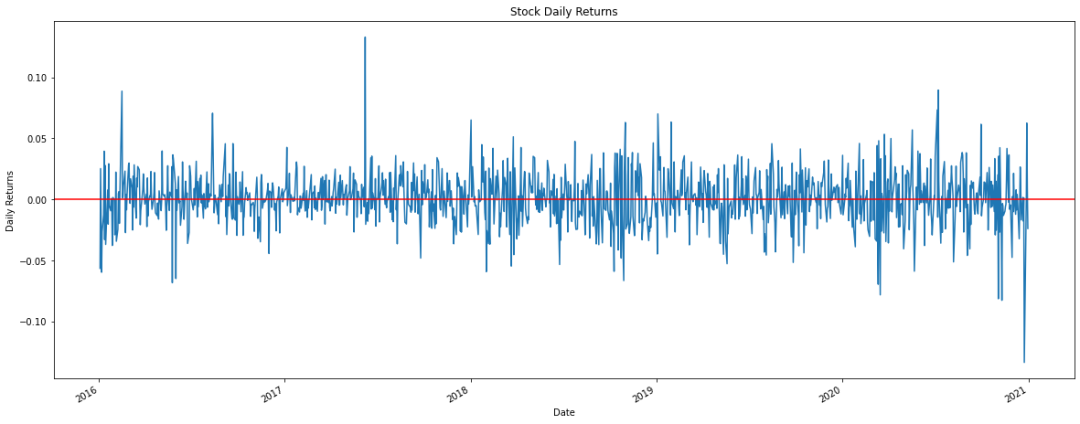
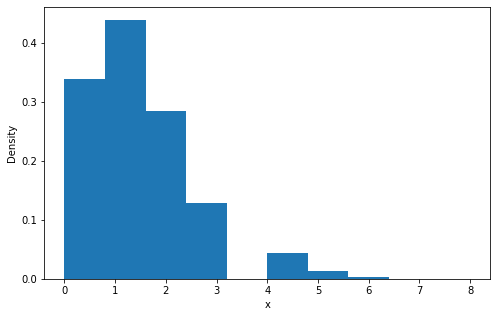
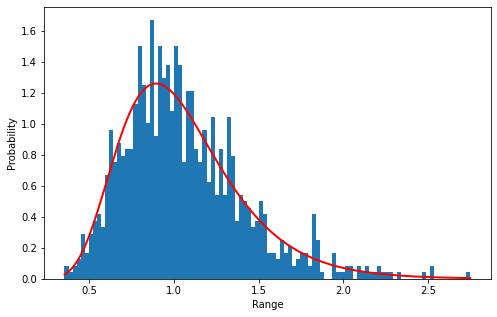
seaborn绘制直方图：先分箱，然后计算每个分箱频数的数据分布。

sns.distplot(df['Returns'].dropna(),bins=100,color='red')

累积概率分布

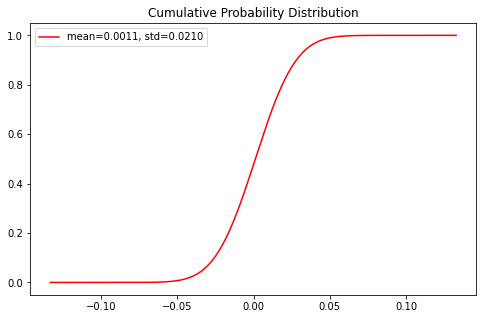
累积概率分布，又称累积分布函数、分布函数等，用于描述随机变量落在任一区间上的概率，常被视为数据的某种特征。
若该变量是连续变量，则累积概率分布是由概率密度函数积分求得的函数。
若该变量是离散变量，则累积概率分布是由分布律加和求得的函数。

param_density = stats.norm.cdf(x, loc=loc, scale=scale)
ax.plot(x, param_density, 'r-', label=label)

均匀分布

它是对称概率分布，在相同长度间隔的分布概率是等可能的。
均匀分布属于连续性概率分布函数，默认为 [0, 1] 的均匀分布。

values = df['Returns'][1:]
s = np.random.uniform(values.min(), values.max(), len(values))
# s = scipy.stats.uniform(loc=values.min(),
#     scale=values.max()-values.min())
count, bins, ignored = plt.hist(s, 15, density=True)
plt.plot(bins, np.ones_like(bins), linewidth=2, color='r')

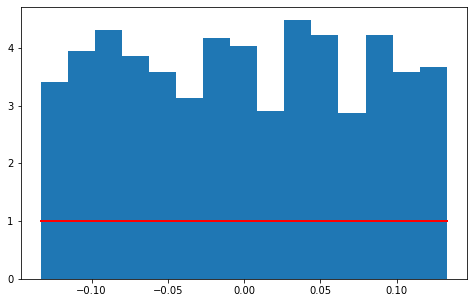
np.ones_like(bins)返回一个用1填充的跟输入形状和类型一致的数组。
np.random.uniform()上(values.min())下(values.max())界的界定范围内随机取len(values)个值

二项分布

二项分布概率密度函数
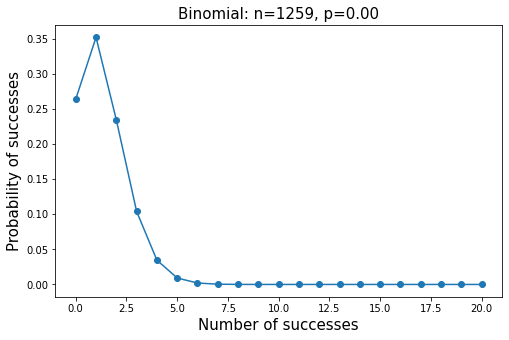
在概率论和统计学中，二项分布是n个独立的成功/失败试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。
PMF(概率质量函数)对离散随机变量的定义，是离散随机变量在各个特定取值的概率。该函数通俗来说，就是对一个离散型概率事件来说，使用该函数来求它各个成功事件结果的概率。
PDF(概率密度函数)是对连续型随机变量的定义，与PMF不同的是，在特定点上的值并不是该点的概率，连续随机概率事件只能求连续一段区域内发生事件的概率，通过对这段区间进行积分，可获得事件发生时间落在给定间隔内的概率

from scipy.stats import binom
n = len(df['Returns'])
p = df['Returns'].mean()
k = np.arange(0,21)

概率质量函数

pmf（k，n，p，loc=0）
# 二项分布
binomial = binom.pmf(k,n,p)
plt.plot(k, binomial, 'o-')

函数模拟二项随机变量

rvs(n, p, loc=0, size=1, random_state=None)

使用rvs函数模拟一个二项随机变量，其中参数size指定要进行模拟的次数。

binom_sim = binom.rvs(n = n, p = p, size=10000)
print("Mean: %f" % np.mean(binom_sim))
print("SD: %f" % np.std(binom_sim, ddof=1))
plt.hist(binom_sim, bins = 10, density = True)

Mean: 1.323600SD: 1.170991

泊松分布

泊松分布的参数是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为
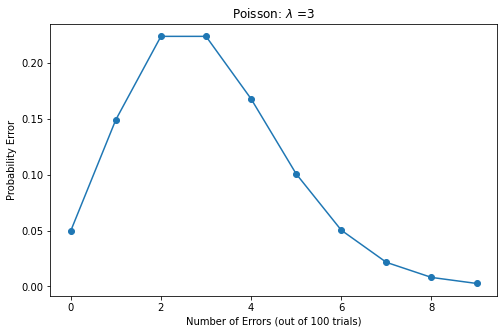
泊松分布概率密度函数

概率质量函数

rate = 3 # 错误率
n = np.arange(0,10) # 实验的数量
y = stats.poisson.pmf(n, rate)
# pmf(k, mu, loc=0)
plt.plot(n, y, 'o-')

模拟泊松随机变量

data = stats.poisson.rvs(mu=3, loc=0, size=100)
#  rvs(mu, loc=0, size=1, random_state=None)
print("Mean: %f" % np.mean(data))
print("Standard Deviation: %f" % np.std(data, ddof=1))
plt.hist(data, bins = 9, density = True, stacked=True)

Mean: 3.210000Standard Deviation: 1.854805

贝塔分布

贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，在机器学习和数理统计学中有重要应用。
贝塔分布是一组定义在区间的连续概率分布。
贝塔分布的概率密度函数是

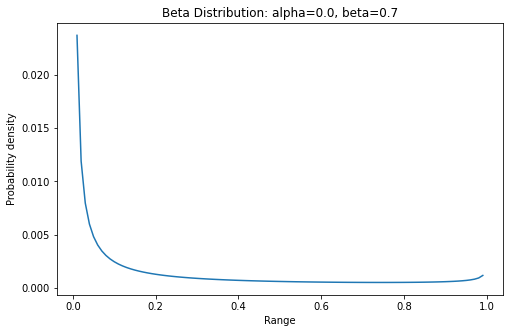
概率密度函数

pdf(x, a, b, loc=0, scale=1)
x = np.arange(0, 1, 0.01)
y = stats.beta.pdf(x, alpha, beta)
plt.plot(x, y)

指数分布

指数分布，也称为负指数分布，是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。

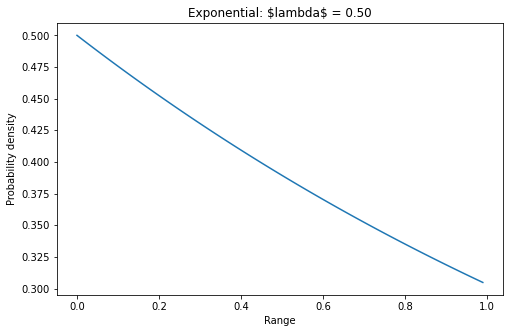
其概率密度函数

lambd = 0.5 # lambda
x = np.arange(0, 1, 0.01)
y = lambd * np.exp(-lambd * x)
plt.plot(x, y)

对数正态分布

是指一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布。对数正态分布从短期来看，与正态分布非常接近。
对数正态分布的概率密度函数

from scipy.stats import lognorm
# 均值
mu = df['Returns'].mean() 
#幅度
sigma = df['Returns'].std()*math.sqrt(252) 
s = np.random.lognormal(mu, sigma, 1000)
count, bins, ignored = plt.hist(s, 100, density=True, align='mid')
x = np.linspace(min(bins), max(bins), 10000)
pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2)) / (x * sigma * np.sqrt(2 * np.pi)))
# pdf=lognorm.pdf(x, s, loc=0, scale=1)
plt.plot(x, pdf, linewidth=2, color='r')

计算分位数

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。

# 计算股票回报率的5%,25%,75%和95%分位数
# 5% 分位数
>>> print('5% quantile', norm.ppf(0.05, mu, sigma))
'5% quantile  -0.548815100072449'
# 75% 分位数
>>> print('75% quantile', norm.ppf(0.75, mu, sigma) )
'75% quantile  0.2265390517243559

统计假设检验

假设(hypothesis)

一般定义：对事物未知事实的一种陈述。如:明天会下雨等
引申到统计学中，所关心的“事物未知事实”是什么?
统计学定义:对总体参数的的数值所作的一种陈述。对总体参数包括总体均值、比例、方差等在分析之前进行陈述。如：假设统计学期末考试的平均成绩等于90分。

假设检验(hypothesis testing)

定义:事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立。
地位:是统计方法(描述性统计和推断性统计) 中推断性统计(参数估计和假设检验)的两大方法之一。
应用:常用于产品生产中，产品质量的检验等问题上。
在假设检验中，先设定原假设(H0)，再设定与其相反的备择假设(H1)。接下来随机抽取样本，若在原假设成立的情况下，样本发生的概率(P)非常小，说明原假设不成立，备择假设成立，则拒绝原假设。否则，接受原假设。

假设检验的过程

(1)提出假设(2)确定适当的检验统计量(3)规定显著性水平(4)计算检验统计量的值(5)作出统计决策
Alpha：显著性水平是估计总体参数落在某一区间内，可能犯错误的概率。是当H0为真时拒绝H0的概率。
p-value：一种概率，一种在原假设为真的前提下出现观察样本以及更极端情况的概率。拒绝原假设的最小显著性水平。
p-value <= alpha：拒绝H0。
p-value > alpha：接受H0。

规定显著性水平

制定决策标准。计算z分布的置信区间。

alpha = 0.05
zleft = norm.ppf(alpha/2, 0, 1)
zright = -zleft  # z分布是对称的
print(zleft, zright)

-1.9599639845400545 1.9599639845400545

计算统计量的值

mu = df['Returns'].mean()
sigma = df['Returns'].std(ddof=1)
n = df['Returns'].shape[0]
# 如果样本容量n足够大，我们可以用z分布代替t分布
# H0为真时，mu = 0 
zhat = (mu - 0)/(sigma/n**0.5)
print(zhat)

1.7823176948718935

作出统计决策

决定是否拒绝原假设。

print('显著水平为{}，我们是否拒绝H0: {}
      '.format(alpha, zhat>zright or zhat<zleft))

显著水平为0.05，我们是否拒绝H0: False

单侧检验

mu = df['Returns'].mean()
sigma = df['Returns'].std(ddof=1)
n = df['Returns'].shape[0]

确定适当的检验统计量。如果样本容量n足够大，可以用z分布代替t分布。

zhat = (mu - 0)/(sigma/n**0.5)
print(zhat)

1.7823176948718935

规定显著性水平。

alpha = 0.05
zright = norm.ppf(1-alpha, 0, 1)
print(zright)
print('显著性水平为{}，我们是否拒绝H0: {}  
      '.format(alpha, zhat>zright))

1.6448536269514722 显著性水平为0.05，我们是否拒绝H0: True

p值检验

p_value = 1 - norm.cdf(zhat, 0, 1)
print(p_value)
print('显著性水平为{}，我们是否拒绝H0: {}
      '.format(alpha, p_value < alpha))

0.03734871936756168 显著性水平为0.05，我们是否拒绝H0: True

scipy.stats中的假设检验

金融股票数据是连续的数据。对于股票数据做假设检验时，是关于比较特征和目标或两个样本。有些假设检验，可以对一个样本进行检验。
连续统计分布清单

Shapiro-Wilk 检验

Shapiro-Wilk检验用于验证一个随机样本数据是否来自正态分布。

from scipy.stats import shapiro
import scipy as sp
W_test, p_value = shapiro(df['Returns'])
# 置信水平为95%，即 alpha=0.05
print('Shapiro-Wilk Test')
print('-'*40)
# 显著性决策
alpha = 0.05
if p_value < alpha:
    print("H0: 样本服从高斯分布")
    print("拒绝H0")
else:
    print("H1: 样本不服从高斯分布")
    print("接受H0")

Shapiro-Wilk Test
H0: 样本服从高斯分布拒绝H0

安德森-达令检验

安德森-达令检验（D’Agostino’s K^2 Test）样本数据是否来自特定分布，包括分布：’norm’, ‘expon’, ‘gumbel’, ‘extreme1’ or ‘logistic’.
零假设H0：样本服从特定分布；备择假设H1：样本不服从特定分布

from scipy.stats import anderson
result = anderson(df['Returns'].dropna())
result

AndersonResult( statistic=6.416543385168325, critical_values=array([0.574, 0.654, 0.785, 0.915, 1.089]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]))

做出决策

D’Agostino’s K^2 Test
统计量: 6.417 15.000: 0.574, 样本不服从正态分布 (拒绝H0) 10.000: 0.654, 样本不服从正态分布 (拒绝H0) 5.000: 0.785, 样本不服从正态分布 (拒绝H0) 2.500: 0.915, 样本不服从正态分布 (拒绝H0) 1.000: 1.089, 样本不服从正态分布 (拒绝H0)

相关性用来检验样本或特征是否相关。因此，检查两个样本或特征是否相关。

F-检验

F检验(F-test)，最常用的别名叫做联合假设检验。它是一种在零假设(H0)之下，统计值服从F-分布的检验。

import scipy
from scipy.stats import f
F = df['Adj Close'].var() / df['Returns'].var()
df1 = len(df['Adj Close']) - 1 
df2 = len(df['Returns']) - 1 
p_value = scipy.stats.f.cdf(F, df1, df2)

做出决策

F-test
Statistic: 1.000 H0: 样本间是相互独立的。 p=1.000

皮尔逊相关系数

皮尔逊相关系数（Pearson’s Correlation Coefficient）也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

适用范围

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：
(1) 两个变量之间是线性关系，都是连续数据。(2) 两个变量的总体是正态分布，或接近正态的单峰分布。(3) 两个变量的观测值是成对的，每对观测值之间相互独立。

from scipy.stats import pearsonr
coef, p_value = pearsonr(df['Open'], 
                    df['Adj Close'])

做出决策

皮尔逊相关系数
相关性检验: 0.999 H1: 样本之间存在相关性。 p=0.000

斯皮尔曼等级相关

斯皮尔曼等级相关是根据等级资料研究两个变量间相关关系的方法。它是依据两列成对等级的各对等级数之差来进行计算的，所以又称为“等级差数法”。
斯皮尔曼等级相关对数据条件的要求没有积差相关系数严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关来进行研究。
斯皮尔曼等级相关系数是反映两组变量之间联系的密切程度，它和相关系数r一样，取值区间[-1,+1]，所不同的是它是建立在等级的基础上计算的。

from scipy.stats import spearmanr
coef, p_value = spearmanr(df['Open'], df['Adj Close'])

做出决策

斯皮尔曼等级相关
斯皮尔曼等级相关系数: 0.997 样本间存在相关性 (拒绝H0) p=0.000

肯德尔等级相关

肯德尔相关(Kendall’s Rank Correlation)系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。
肯德尔相关系数的取值范围在-1到1之间

当τ为1时，表示两个随机变量拥有一致的等级相关性；
当τ为-1时，表示两个随机变量拥有完全相反的等级相关性；
当τ为0时，表示两个随机变量是相互独立的。
```
from scipy.stats import kendalltau
coef, p_value = kendalltau(df['Open'], 
                df['Adj Close'])
```
做出决策

肯德尔等级相关
肯德尔等级相关系数: 0.960 样本间存在相关性 (拒绝H0) p=0.000

卡方检验

卡方检验(Chi-Squared Test)是用途非常广的一种假设检验方法，它在分类资料统计推断中的应用，包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
在大数据运营场景中，通常用在某个变量(或特征)值是不是和因变量有显著关系。

from scipy.stats import chi2_contingency
from scipy.stats import chi2
stat, p_value, dof, expected = chi2_contingency(df[['Open','Low','High','Adj Close','Volume']])
prob = 0.95
critical = chi2.ppf(prob, dof)

统计量决策

abs(stat) >= critical
dof=5032
可能性=0.950,
critical=5198.140, stat=259227.557
两者具有相关性 (拒绝H0)

p值决策

p <= alpha
显著性=0.050, p=0.000
两者具有相关性 (拒绝H0)

这部分是比较两个样本或特征;得到结果并检查它们是否都是独立样本。

scipy.stats中其他假设检验

Box-Cox Power Transformation

Box cox Transformation可以将非正态分布的独立因变量转换成正态分布，很多统计检验方法的一个重要假设就是“正态性”，所以当对数据进行Box cox Transformation后，这意味着可以对数据进行许多种类的统计检验。
Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的。

>>> from scipy.stats import boxcox
>>> df['boxcox'], lam = boxcox(df['Adj Close'])
>>> print('Lambda: %f' % lam)

Lambda: -0.119624

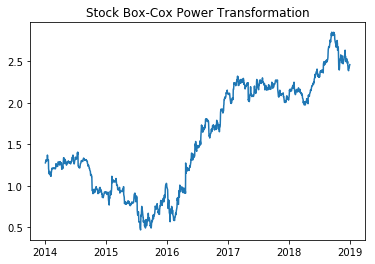
折线图

plt.plot(df['boxcox'])

直方图

plt.hist(df['boxcox'])

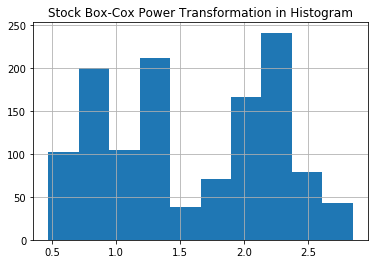
下面几个假设检验只简单力矩其使用方法，不做太多其他解释。

# 参数假设检验
# Student’s t-Test
# 这是对原假设的双侧检验，两个独立的样本有相同
# 的平均值(期望值)。
# 这个测试假设总体默认具有相同的方差。
from scipy.stats import ttest_ind
stat, p_value = ttest_ind(df['Open'], 
    df['Adj Close'])
# Paired Student’s t-test
# 这是对原假设的双侧检验，
# 即两个相关或重复的样本具有相同的平均值(期望值)
from scipy.stats import ttest_rel
stat, p_value = ttest_rel(df['Open'],
    df['Adj Close'])
# Analysis of Variance Test (ANOVA)
from scipy.stats import f_oneway
stat, p_value = f_oneway(df['Open'], 
    df['Adj Close'], df['Volume'])
# 非参数假设检验
# Mann-Whitney U Test
from scipy.stats import mannwhitneyu
stat, p_value = mannwhitneyu(df['Open'], 
    df['Adj Close'])
# Wilcoxon Signed-Rank Test
from scipy.stats import wilcoxon
stat, p_value = wilcoxon(df['Open'], 
    df['Adj Close'])
# Kruskal-Wallis Test
from scipy.stats import kruskal
stat, p_value = kruskal(df['Open'], 
    df['Adj Close'], df['Volume'])
# Levene Test
from scipy.stats import levene
stat, p_value = levene(df['Open'], 
    df['Adj Close'])
# Mood's Test
from scipy.stats import mood
stat, p_value = mood(df['Open'], 
    df['Adj Close'])
# Mood’s median test
from scipy.stats import median_test
stat, p_value, med, tbl = median_test(df[
  'Open'], df['Adj Close'], df['Volume'])
# Kolmogorov-Smirnov test
from scipy.stats import ks_2samp
stat, p_value = ks_2samp(df['Open'], 
    df['Adj Close'])

Scipy 与数据统计分析基础

准备

模块

数据准备

特征创造

统计分析

Mean 均值

Median 中位数

Mode 众数

Range 全距

Variance 方差

Standard 标准差

Standard error 标准误差

Z-Scores

Contingency Table 列联表

Scatter plot 散点图

Regression 回归

初等概率论预测结果

蒙特卡罗方法

随机变量和概率分布

累积分布

概率密度函数

累积概率分布

均匀分布

二项分布

概率质量函数

函数模拟二项随机变量

泊松分布

概率质量函数

模拟泊松随机变量

贝塔分布

概率密度函数

指数分布

其概率密度函数

对数正态分布

计算分位数

统计假设检验

假设(hypothesis)

假设检验(hypothesis testing)

假设检验的过程

规定显著性水平

计算统计量的值

作出统计决策

单侧检验

p值检验

scipy.stats中的假设检验

Shapiro-Wilk 检验

Shapiro-Wilk Test

安德森-达令检验

做出决策

D’Agostino’s K^2 Test

F-检验

做出决策

F-test

皮尔逊相关系数

适用范围

做出决策

皮尔逊相关系数

斯皮尔曼等级相关

做出决策

斯皮尔曼等级相关

肯德尔等级相关

做出决策

肯德尔等级相关

卡方检验

统计量决策

p值决策

scipy.stats中其他假设检验

Box-Cox Power Transformation

折线图

直方图