PyTorch
requires_grad、volatile、detach()/detach_()三个标志为中，最关键的就是 requires_grad，另外两个都可以转化为 requires_grad 来理解。
retain_graph、retain_variables、create_graph 三个标志位，与计算图的保持与建立有关系。其中 retain_variables 与 retain_graph等价，retain_variables 会在PyTorch新版本中被取消掉。

1、requires_grad 的含义及标志位说明

requires_gard 是Tensor变量的一个属性，一般默认为False。另外，0.4.0版本的 Pytorch 将 Variable 和 Tensor 合并，统称为 Tensor，在过去的版本中，requires_grad属性是Variable封装的属性

  • 如果对于某Variable 变量 x ，其 x.requires_grad == True，则表示它可以参与求导，也可以从它向后求导。默认情况下，一个新的Variables 的 requires_grad 和 volatile 都等于 False
  • requires_grad == True 具有传递性：如果：x.requires_grad == True，y.requires_grad == False ，z=f(x,y)则， z.requires_grad == True
  • 凡是参与运算的变量（包括输入量，中间输出量，输出量，网络权重参数等），都可以设置 requires_grad
  • volatile==True 就等价于 requires_grad==False 。volatile==True 同样具有传递性。一般只用在inference过程中。若是某个过程，从 x 开始都只需做预测，不需反传梯度的话，那么只需设置x.volatile=True，那么 x 以后的运算过程的输出均为 volatile==True，即 requires_grad==False 。虽然inference 过程不必backward()，所以requires_grad 的值为False 或 True，对结果是没有影响的，但是对程序的运算效率有直接影响；所以使用volatile=True，就不必把运算过程中所有参数都手动设一遍requires_grad=False 了，方便快捷
  • detach() ，如果 x 为中间输出，x' = x.detach 表示创建一个与 x 相同，但requires_grad==False 的variable，(实际上是把x’ 以前的计算图 gradfn 都消除了)，x’ 也就成了叶节点。原先反向传播时，回传到x时还会继续，而现在回到x’处后，就结束了，不继续回传求到了。另外值得注意，x (variable类型) 和 x’ (variable类型)都指向同一个Tensor，即 x.data，而`detach()` 表示不创建新变量，而是直接修改 x 本身

  • retain_graph ，每次 **backward()** 时，默认会把整个计算图free掉。一般情况下是每次迭代，只需一次 forward() 和一次 backward()，前向运算forward() 和反向传播backward()是成对存在的，一般一次backward()也是够用的。但是不排除，由于自定义loss等的复杂性，需要一次forward()，多个不同loss的backward()来累积同一个网络的grad，来更新参数。于是，若在当前backward()后，不执行forward() 而可以执行另一个backward()，需要在当前backward()时，指定保留计算图，即backward(retain_graph)

    2、反向求导和权重更新

  • 求导和优化（权重更新）是两个独立的过程，只不过优化时一定需要对应的已求取的梯度值。所以求得梯度值很关键，而且，经常会累积多种loss对某网络参数造成的梯度，一并更新网络

  • 反向传播过程中，肯定需要整个过程都链式求导。虽然中间参数参与求导，但是却可以不用于更新该处的网络参数。参数更新可以只更新想要更新的网络的参数
  • 如果obj是函数运算结果，且是标量，则 obj.backward() （注意，backward()函数中没有填入任何tensor值，就相当于 backward(torch.tensor([1])))

  • 对于继承自 nn.Module 的某一网络 net 或网络层，定义好后，发现默认情况下，net.paramters 的requires_grad 就是 True 的（虽然只是实验证明的，还未从源码处找到证据），这跟普通的Variable张量不同。因此，当x.requires_grad == False , y = net(x) 后，有 y.requires_grad == True ；但值得注意，虽然nn.xxloss和激活层函数，是继承nn.Module的，但是这两种并没有网络参数，就更谈不上 paramters.requires_grad 的值了。所以类似这两种函数的输出，其requires_grad只跟输入有关，不一定是 True

    3、计算图相关

  • 计算图就是模型前向forward() 和后向求梯度backward() 的流程参照

  • 能获取回传梯度(grad)的只有计算图的叶节点。注意是获取，而不是求取。中间节点的梯度在计算求取并回传之后就会被释放掉，没办法获取。想要获取中间节点梯度，可以使用 register_hook （钩子）函数工具。当然， register_hook 不仅仅只有这个作用
  • 只有标量才能直接使用 **backward()**，即loss.backward()，pytorch 框架中的各种nn.xxLoss()，得出的都是minibatch 中各结果平均/求和后的值。如果使用自定义的函数，得到的不是标量，则backward()时需要传入 grad_variable 参数
  • 经常会有这样的情况：x1 —> |net1| —> y1 —> |net2| —> z1，net1 和 net2 是两个不同的网络。x1 依次通过两个网络运算，生成 z1 。比较担心一次性运算后，再backward()，是不是只更新 net1而不是net1、net2都更新呢？类比 x2 —> |f1| —> y2 —> |f2| —> z2， f1、f2 是两个普通的函数，z2=f2(y2) , y2=f1(x2)

按照以下格式实验：

  1. w1 = torch.Tensor([2]) #认为w1 与 w2 是函数f1 与 f2的参数
  2. w1 = Variable(w1,requires_grad=True)
  3. w2 = torch.Tensor([2])
  4. w2 = Variable(w2,requires_grad=True)
  5. x2 = torch.rand(1)
  6. x2 = Variable(x2,requires_grad=True)
  7. y2 = x2**w1 # f1 运算
  8. z2 = w2*y2+1           # f2 运算
  9. z2.backward()
  10. print(x2.grad)
  11. print(y2.grad)
  12. print(w1.grad)
  13. print(w2.grad)

发现 x2.grad，w1.grad，w2.grad 是个值 ，但是 y2.grad却是None，说明x2,w1,w2的梯度保留了，y2的梯度获取不到。实际上，仔细想一想会发现，x2,w1,w2均为叶节点。在这棵计算树中 ，x2 与w1 是同一深度(底层)的叶节点，y2与w2 是同一深度，w2 是单独的叶节点，而 y2 是 x2 与 w1 的父节点，所以只有y2没有保留梯度值， 印证了之前的说法。同样这也说明，计算图本质就是一个类似二叉树的结构。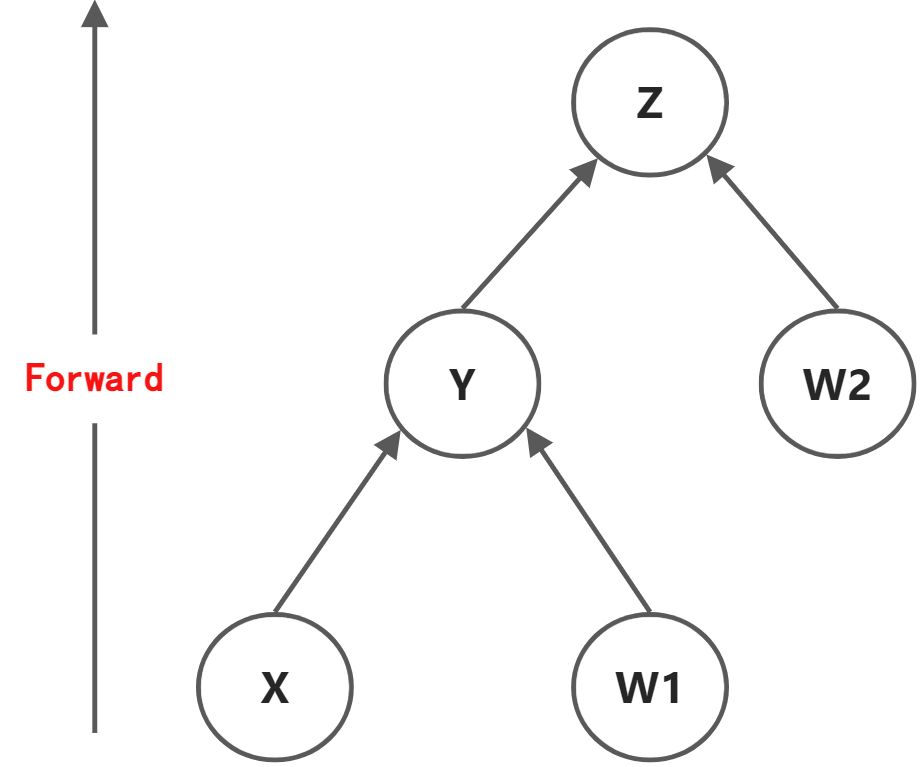
PyTorch中的backward() - 图1
那么对于两个网络，会是怎么样呢？使用pytorch 的cifar10 例程，稍作改动做了实验。把例程中使用的一个 Alexnet 拆成了两个net ——— net1 和 net2 。

  1. optimizer = torch.optim.SGD(itertools.chain(net1.parameters(), net2.parameters()),lr=0.001, momentum=0.9) # 这里 net1 和net2 优化的先后没有区别 ！！
  3. optimizer.zero_grad() #将参数的grad值初始化为0
  5. # forward + backward + optimize
  6. outputs1 = net1(inputs) #input 未置requires_grad为True，但不影响
  7. outputs2 = net2(outputs1)
  8. loss = criterion(outputs2, labels) #计算损失
  9. loss.backward() #反向传播
  11. print("inputs.requires_grad:")
  12. print(inputs.requires_grad) # False
  13. print("the grad of inputs:")
  14. print(inputs.grad) # None
  16. print("outputs1.requires_grad:")
  17. print(outputs1.requires_grad) # True
  18. print("the grad of outputs1:")
  19. print(outputs1.grad) # None
  21. print("the grad of net1:")
  22. print(net1.conv1.bias.grad) # no-None
  23. print("the grad of net2:")
  24. print(net2.fc3.bias.grad) # no-None
  26. optimizer.step() #用SGD更新参数

后缀注释就是打印的结果。可以看出，只有网络参数的grad是直接可获取的。而且是两个网络都可以获取grad 值，获取grad后，当然就可以更新网络的参数了，两个网络都是可以更新的。
类比上边例子的解释，两个网络其实就是处在叶节点的位置，只不过深度不同。同理，网络内部的运算，每一层网络权重参数其实也是处在叶节点上，只不过在树中的深度不同罢了，前向运算时按照二叉树的结构，不断生成父节点。
事实上，原先是以为网络与普通函数不同，因为它具有register_xx_hook()这个类函数工具，所以认为它可以默认保存权重参数的grad来用于更新，后来才明白，本质上与普通函数的参数一样，都是处在叶节点，就可以保存参数的grad，至于register_xx_hook()，看来是另做它用，或者说用register_xx_hook()可以记录甚至更改中间节点的grad值。

4、一些特殊情况

如果想把网络某一部分参数固定，不让其被训练，可以使用requires_grad。

  1. for p in sub_module.parameters():
  2.     p.requires_grad = False

可以这样理解，因为是叶节点（而不是中间节点），所以不求grad（grad为'None'），也不会影响网络的正常反向传播。