机器学习

偏差-方差权衡

x——样本特征数据;
y——响应测量值;
——测量误差，假设为均值0，标准差的独立噪声。
假设建模是寻找y与x之间的关系

衡量模型性能时常用的是平方误差，也就是模型输出与真实响应的误差

image.png
平方误差的分解

∵ 是独立噪声且
∴

∵是确定的
∴
∵统计平均是均值的无偏估计
∴
最终模型的误差只剩下了三个非误差项：

第一项真实模型与模型均值之差的平方和再求均值，显然括号内是肯定的，均值运算符可以直接拿掉，所以第一项就等于真实模型与模型均值之差的平方，给他一个专门的名称，叫偏差的平方。
第二项，对测量的误差求均值，不要忘记误差是均值为0的随机变量，所以第二项就是测量误差的方差。
第三项，模型均值与模型之差的平方再求均值，这是一个典型的方差定义式，所以就是模型的方差。
所以可以得到如下公式：

于是反应模型性能的平方误差最终由三个因素来决定，就是偏差、噪声方差和模型方差，其中噪声方差是独立元素，这里不做讨论，主要关注偏差和模型方差这两个。

偏差-变异性权衡

偏差

衡量模型的准确性
偏差指的是模型输出与真实值之间的差异，所以偏差的计算一定需要有标签数据，也意味着主要在有监督学习模型的建模阶段，偏差是所建立的模型精确性的衡量。低的偏差意味着更高的精确性，高的偏差则意味着更低的精确性。

方差/变异性

衡量模型的变异性、可泛化性
模型方差反应的是模型应用于不同的数据时的变异性大小，或者说模型的泛化能力。

偏差-方差困境

偏差
方差

  • 若追求低偏差，得到高方差
  • 若追求低方差，得到大偏差

以一个具体的线性回归的例子来说明一下：

  1. import pandas as pd
  2. import numpy as np
  3. from matplotlib import pyplot as plt
  4. import seaborn as sns
  5. %matplotlib inline
  6. df=pd.read_csv('C:\Python\Scripts\my_data\iris.csv',header=None,
  7.                names=['sepal_length','sepal_width','petal_length','petal_width','target'])
  8. my_data=df[['sepal_length','sepal_width']].iloc[:50]
  9. # sns.lmplot函数在回归的同时可以将样本散点图散点图和回归线同时画出来
  10. sns.lmplot(x='sepal_length',y='sepal_width',data=my_data,ci=None)
  11. #order 默认为 1，线性拟合

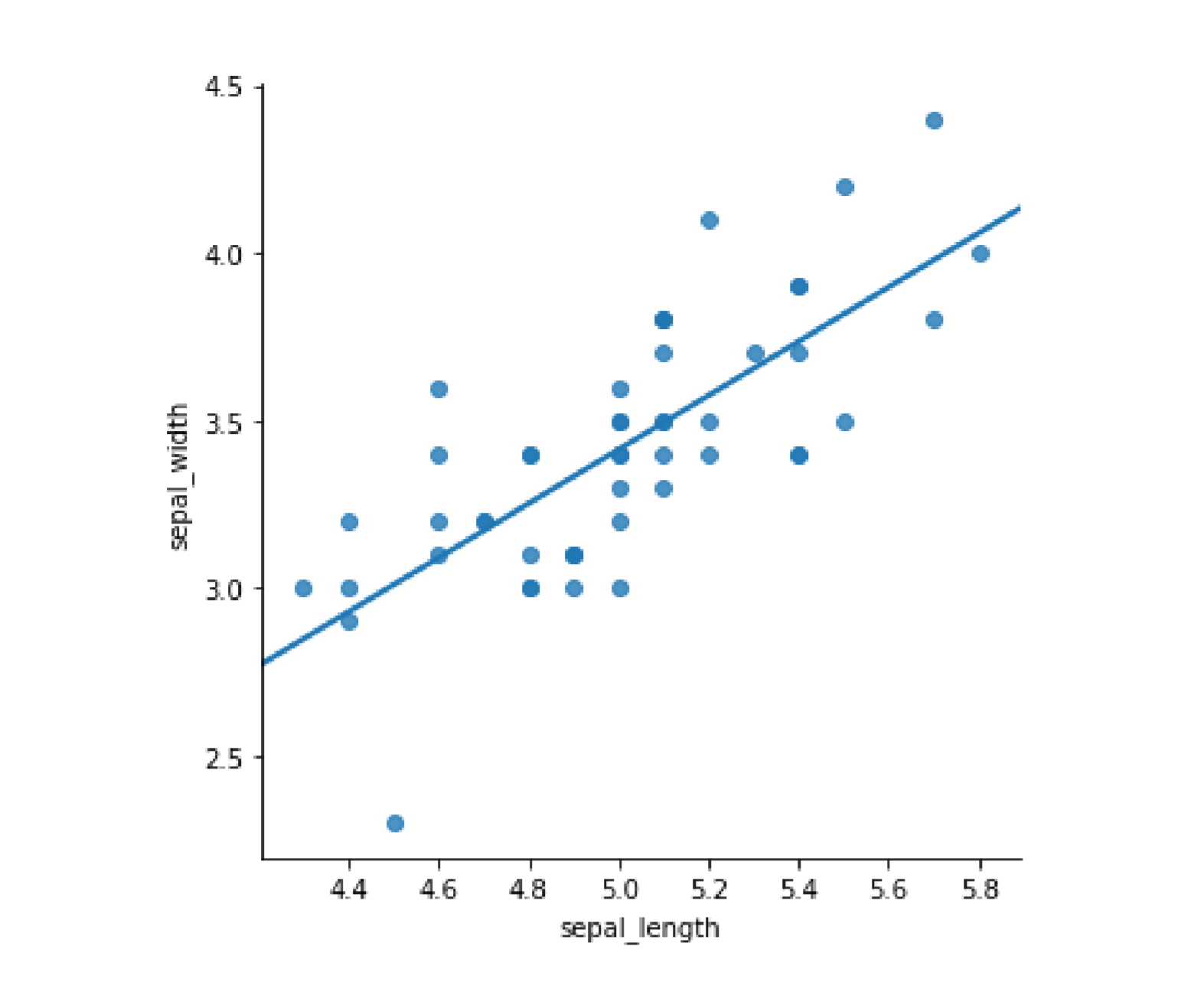
image.png
假装给他们打标签，随机的分为两类，然后对这两类分别做线性回归

  1. my_data['sample']=np.random.randint(1,3,len(my_data))
  2. my_data.head()
  3. my_data.groupby('sample')[['sepal_length','sepal_width']].mean()
  4. sns.lmplot(x='sepal_length',y='sepal_width',data=my_data,ci=None,hue='sample')

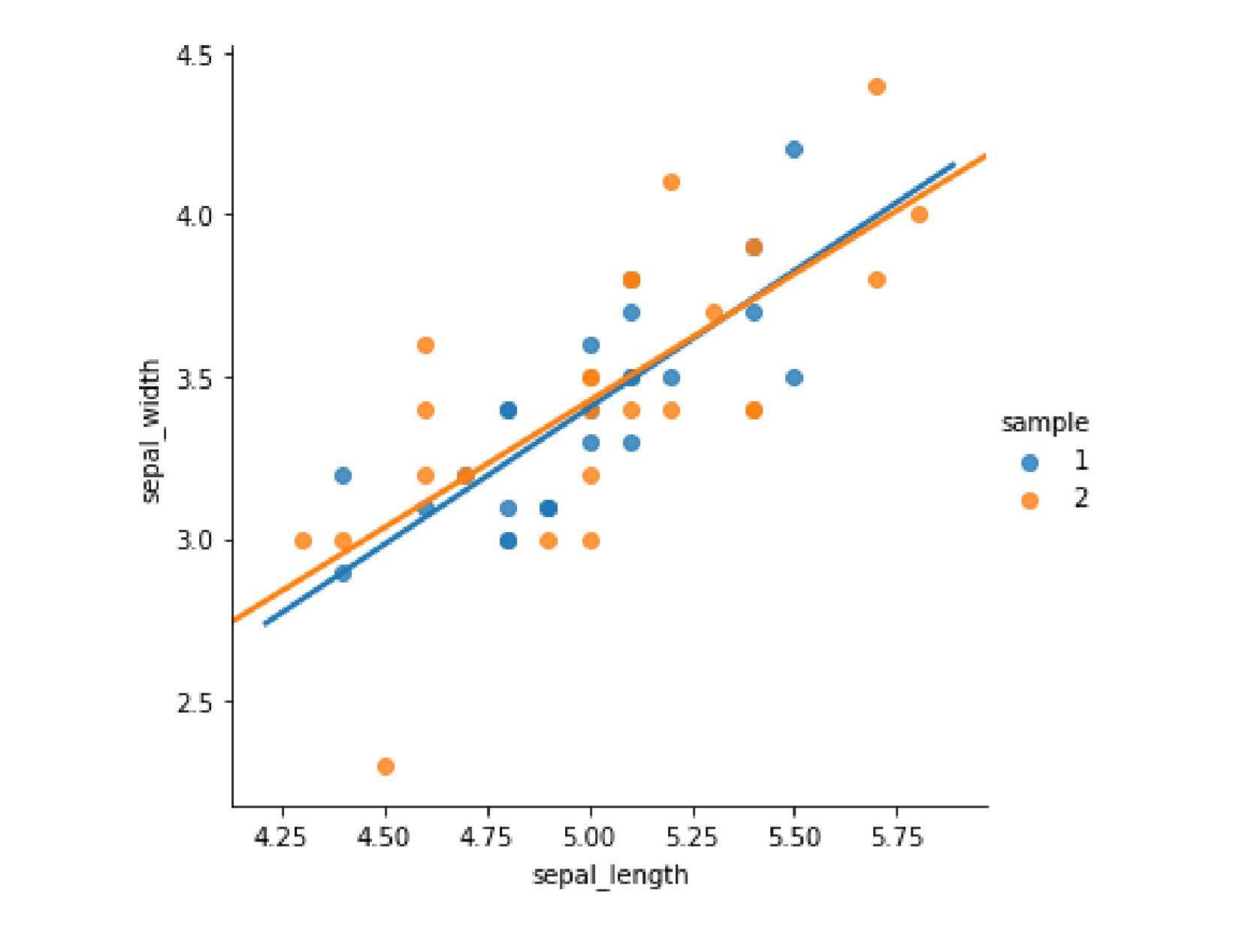
image.png
图中不同的颜色代表不同的随机标签，可以从图中看出，两类数据其实是来源于同一分布，尽管数据间有个体差异，但两个线性回归之间的差异并不大，但是模型的偏差值较大，也就是大部分的点都远离他们的回归线，如果不做线性回归，把回归的阶数order设置为6

  1. sns.lmplot(x='sepal_length',y='sepal_width',data=my_data,ci=None,hue='sample',order=6)
  2. plt.ylim(2.5,4.5)

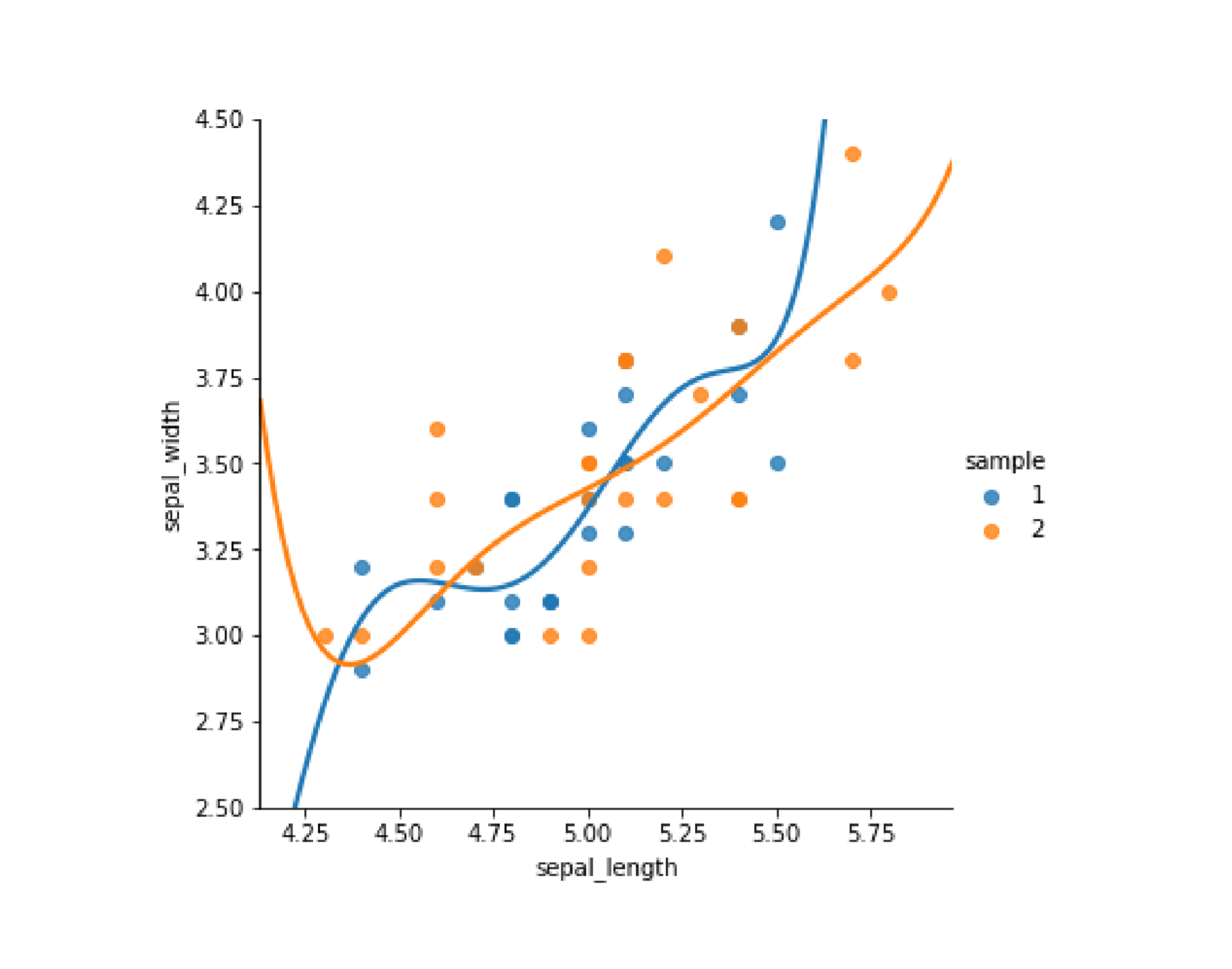
image.png
可以看到两条曲线更加迎合自己所在的散点位置，模型偏差变小了，但是两条回归曲线却展现出很大的差异。例如sepal length小于2.5的那些点，两个模型预测的sepal width会南辕北辙。然而事实上，两组样本源于同一分布，仅仅是采样的不同就导致了模型的巨大差异，显然这样的模型对数据过于敏感，变异性太大泛化性是很差的。这体现的就是方差-偏差困境。

模型的平方误差

  • 偏差——建模阶段模型与真实响应的偏差
  • 方差——模型面临不同数据时的变异性

  • 噪声

    实际应用中偏差-方差困境带来的问题

  • 模型在训练集上的精确度

  • 面临新数据时的泛化能力

    RMSE：模型性能的衡量

    根据RMSE的数学定理，自定义一个多项式拟合的RMSE函数，这个自定义函数中，三个参数：x一一预测变量、y——真实响应、coefs——多项式系数。
    函数中先根据预测变量和多项式系数来求出模型的响应，这里多项式求值使用的是np.polyval函数，然后根据模型响应和真实响应的差别求出rmse，

    1. def rmse(x, y, coefs):
    2.   yfit=np.polyval(coefs, x)
    3.   rmse=np.sqrt(np. mean((y-yfit)**2))
    4.      return rmse

    这里还是使用鸢尾花的前五十个样本，这里将五十个数据作随机划分，一半做训练集，一半作测试集，然后依次构造阶数为1-7的多项式模型，对训练集数据作多项式拟合，然后在拟合出的结果分别计算训练集和测试集的rmse，这里多项式拟合使用的是np.polyval函数，输入参数中指定独立变量，真实响应以及多项式阶数就可以获得多项式系数，而且这个系数是支持在np.polyval函数中直接使用的。最后把不同阶次模型的训练集rmse和测试集rmse在同一张图中画出来。

    1. from sklearn.model_selection import train_test_split
    2. import numpy as np
    3. import pandas as pd
    4. from matplotlib import pyplot as plt
    5. df=pd.read_csv('C:\Python\Scripts\my_data\iris.csv',header=None,names=['sepal_length','sepal_width','petal_length','petal_width','target'])
    6. my_data=df[['sepal_length','sepal_width']].iloc[:50]
    7. def rmse(x,y,coefs): # 注意，自定义函数的语法
    8.   yfit=np.polyval(coefs,x)
    9.   rmse=np.sqrt(np.mean((y-yfit)**2))
    10.   return rmse
    11. xtrain,xtest,ytrain,ytest=train_test_split(my_data['sepal_length'],my_data['sepal_width'],test_size = 0.5)
    12. train_err=[]
    13. validation_err=[]
    14. degrees=range(1,8)
    15. for i,d in enumerate(degrees):
    16.   p=np.polyfit(xtrain,ytrain,d)
    17.   train_err.append(rmse(xtrain,ytrain,p))
    18.   validation_err.append(rmse(xtest,ytest,p))
    19. fig,ax=plt.subplots()
    20. ax.plot(degrees,validation_err,lw=2,label='testing error')
    21. ax.plot(degrees,train_err,lw=2,label='training error')
    22. ax.legend(loc=0)
    23. ax.set_xlabel('degree of polynomial')
    24. ax.set_ylabel('RMSE')

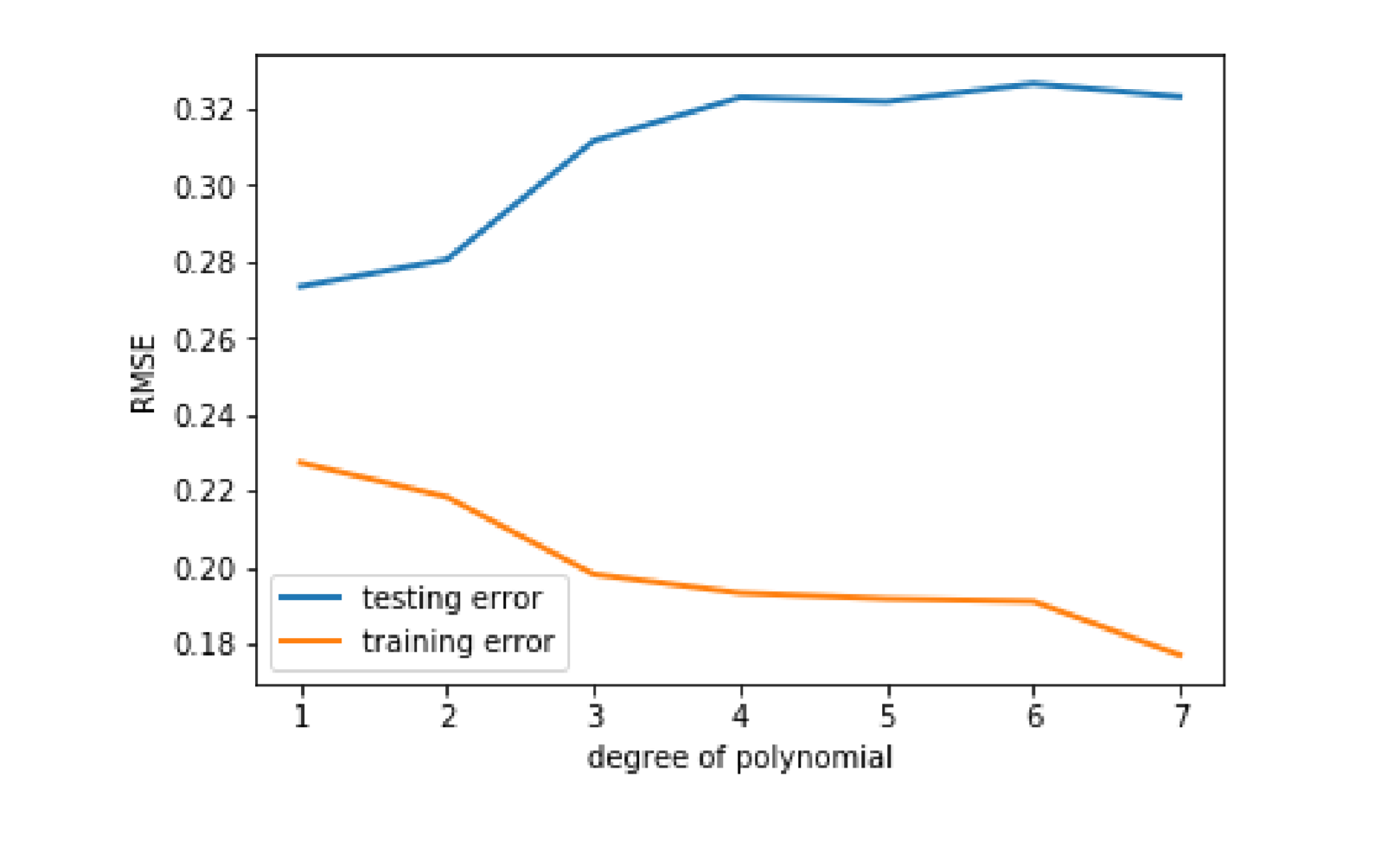
    image.png
    图中以模型阶次为横轴，rmse为纵轴，黄色直线代表训练集rmse，蓝色直线代表测试集rmse。从结果的图中可以看到，随着模型阶次的身高呈现略微下降的趋势，然而蓝色的线，也就是测试集的rmse在大幅的上升。这则是方差偏差困境的极端情况。

    过拟合与欠拟合

    当建模过程中，也就是训练集过程中，一味提高模型复杂度来追求低偏差时，模型面临的有差异的数据时，例如这里的测试集，性能反而大大下降。这种在训练集上性能很好，而在测试集上性能下降严重，泛化能力差的极端现象，一般称为过拟合（Overfitting）。
    与过拟合相对的，模型过于简单，尽管稳定，却即使在训练集偏差有过大现象称之为欠拟合。

    解决途径

    Underfitting

  • 增加模型的复杂程度

  • 增加特征

Overfitting

  • 降低模型复杂程度
  • 增加样本容量

过拟合和欠拟合依然反应的是偏差和方差权衡的问题，有监督学习在的总误差，偏差项和方差项可以用下图表示：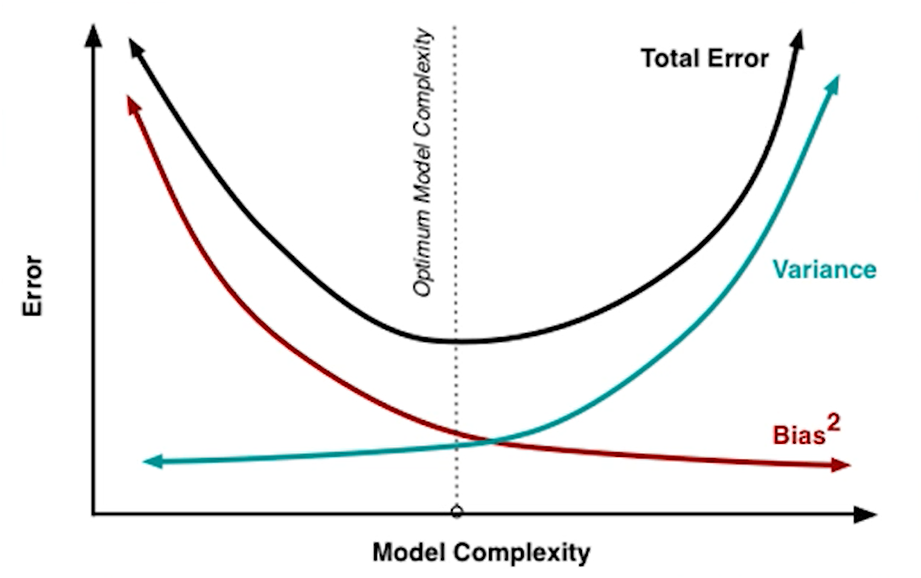
image.png
从图中可以看到，随着模型复杂度的升高，模型的偏差项会变小，但是方差项会升高，但一般而已会存在一个最优点，使得两者达到一个折中，总误差最小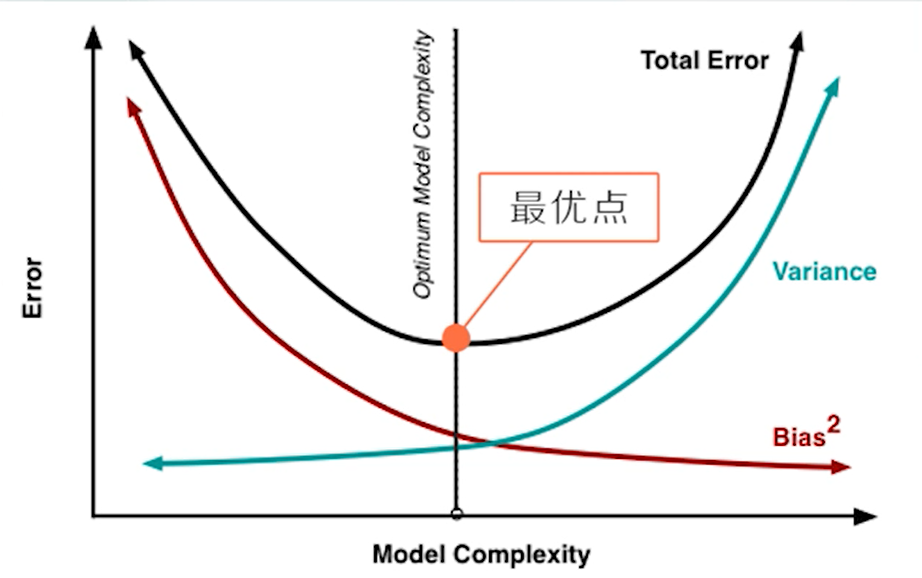
image.png
所谓的偏差方差权衡就是要找到这个最优点。
偏差-方差困境中如何评价模型?其中K折交叉验证就是一种最常用的策略。

K折交叉验证

K折交叉验证的步骤

  1. 对数据做K等份划分
  2. 其中1份作为测试集，剩下的K-1份作为训练集
  3. 换1份作为测试集，剩下的K-1份作为训练集
  4. 测试集遍历每一份，即共做K次训练-测试，模型性能为K次平均

用图来理解K折交叉验证中数据的划分

  1.  from sklearn.model_selection import KFold
  2. my_data=df[['sepal_length','sepal_width']]
  3. nfolds=3
  4. fig,axes=plt.subplots(1,nfolds,figsize=(14,4))
  5. kf=KFold(n_splits =nfolds)
  6. i=0
  7. for training, validation in kf.split(my_data):
  8.     x,y=my_data.iloc[training]['sepal_length'],df.iloc[training]['sepal_width']
  9.     axes[i].plot(x,y,'ro')
  10.     x,y=my_data.iloc[validation]['sepal_length'],df.iloc[validation]['
  11.     sepal_width']
  12.     axes[i].plot(x,y,'bo')
  13.     i=i+1
  14. plt.tight_layout()

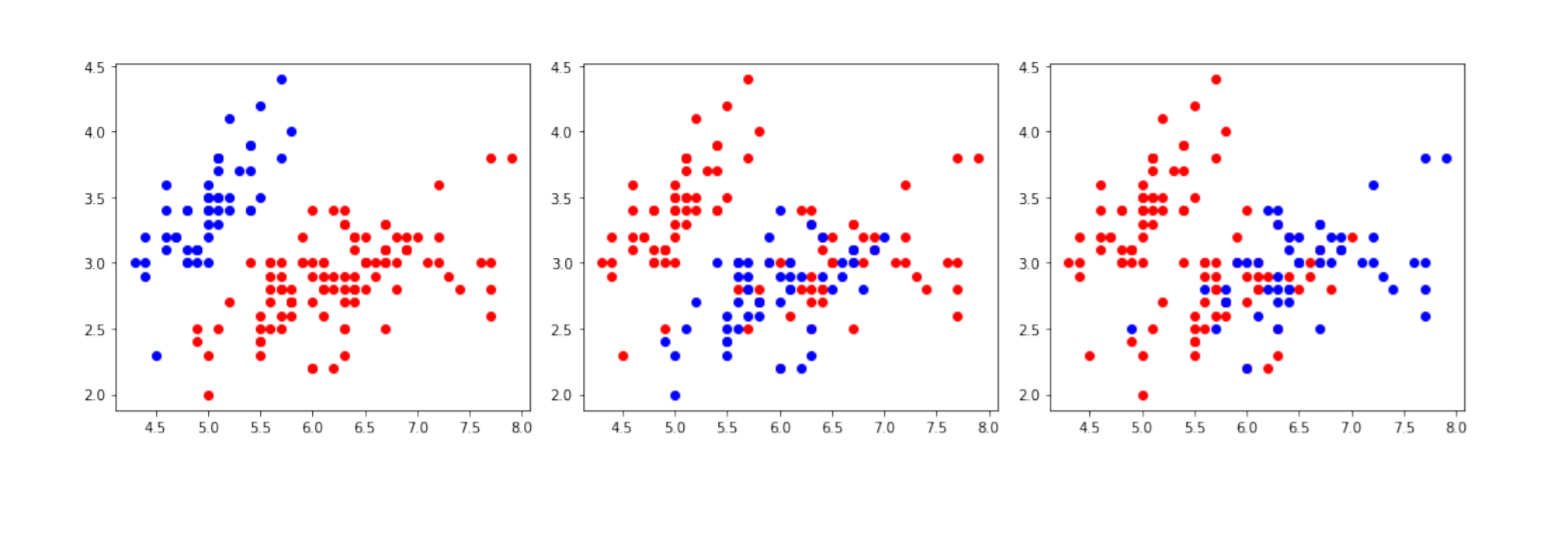
image.png
这幅图三个子图中所包含的数据集是完全一样的，都是150个鸢尾花，以sepal_length为横轴sepal_width为纵轴的散点图，每一副子图都代表一次模型训练加验证时的数据划分，其中红色的点是训练集，蓝色的点则是测试集数据，所以3折交叉验证刚好对应三副不同的子图，可以看到每个数据在三幅图中有两次红色也就是训练模型的集汇和一次蓝色，也就是测试模型的集汇。
再来看一个例子， sklearn.model_selection 库中的 cross_val_score 函数可以实现k折交叉验证。对150个鸢尾花数据建立一个KNN（也就是K邻近点模型），简单来说KNN就是用距离样本最近的k个数据即近邻点的响应作为数据的响应。 sklearn.neighbors 库中的 KNeighborsClassifier 对象可以直接拿来应用，分别创建两个KNeighborsClassifier模型，一个用全部的数据来训练，然后用同一批建模数据来测所得模型的性能。

  1. from sklearn.model_selection import cross_val_score,train_test_split
  2. from sklearn.neighbors import KNeighborsClassifier
  3. knn1 = KNeighborsClassifier(n_neighbors=1)
  4. knn2 = KNeighborsClassifier(n_neighbors=1)
  5. knn1.fit(my_data[['sepal_length','sepal_width']],my_class) # 全部数据用来训练
  6. print('训练集测试集相同时，模型的性能得分是：',knn1.score(my_data[['sepal_length','
  7. sepal_width']],my_class))# 在训练集上评价性能
  8. print('\n')scores=
  9. cross_val_score(knn2,my_data[['sepal_length','sepal_width']],my_class,cv=5,
  10. scoring='accuracy') # 交叉验证
  11. print('5 折交叉验证时，模型的性能平均得分是：',
  12. scores.mean())

image.png
可以看到这个模型的得分接近0.93，但是当使用五折交叉验证来训练模型时，五次下来的平均成绩只有0.73，远远低于之前的成绩，但是由于在交叉验证中使用的是模型没有见过的数据来测试模型，五次重复下来对模型的评价要比第一个模型客观公正的多。
因为在真正应用模型的时候，由于采样差异和测量噪声的存在是很难遇到于训练数据一模一样的情况。
先来看一个简单的例子：

  1. import numpy as np
  2. import pandas as pd
  3. from matplotlib import pyplot as plt
  4. from sklearn.neighbors import KNeighborsClassifier
  5. from sklearn.model_selection import cross_val_score
  6. df=pd.read_csv('C:\Python\Scripts\my_data\iris.csv',header=None,
  7. names=['sepal_length','sepal_width','petal_length','petal_width','target'])
  8. my_data=df[['sepal_length','sepal_width']]
  9. my_class=[]
  10. for n in range(150):
  11.     if n<50:
  12.         my_class.append(1)
  13.     elif n<100:
  14.         my_class.append(2)
  15.     else:
  16.         my_class.append(3)
  17. k_range=range(1,30)
  18. errors=[]
  19. for k in k_range:
  20.     knn=KNeighborsClassifier(n_neighbors=k)
  21.     # cross_val_score函数实现k值交叉验证，并求出模型的平均性能等等
  22.     scores=cross_val_score(knn,df[['sepal_length','sepal_width']],my_class,cv=5,
  23.     scoring='accuracy')
  24.     accuracy=np.mean(scores)
  25.     # 选取的模型出错率=1-准确率作为评价指标
  26.     error=1-accuracy
  27.     errors.append(error)
  28. plt.figure()
  29. plt.plot(k_range,errors) # 从图看 KNN 中近邻数对 error 的影响
  30. plt.xlabel('k')
  31. plt.ylabel('error rates')

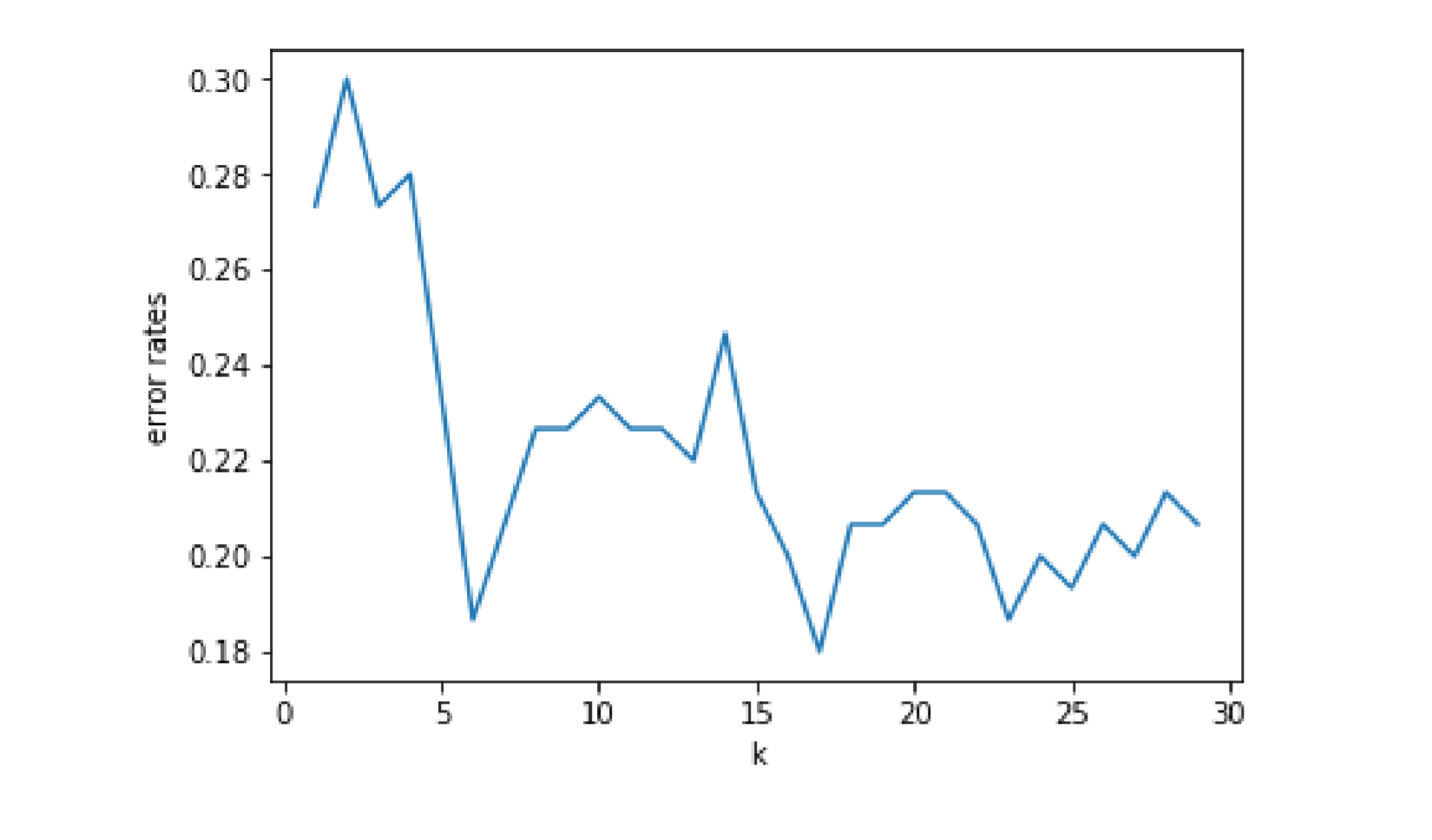
image.png
通过结果的图可以看到，随着近邻数k的增加，出错率开始是整体下降趋势，然后大于等于7以后又呈现出一定的震荡和反复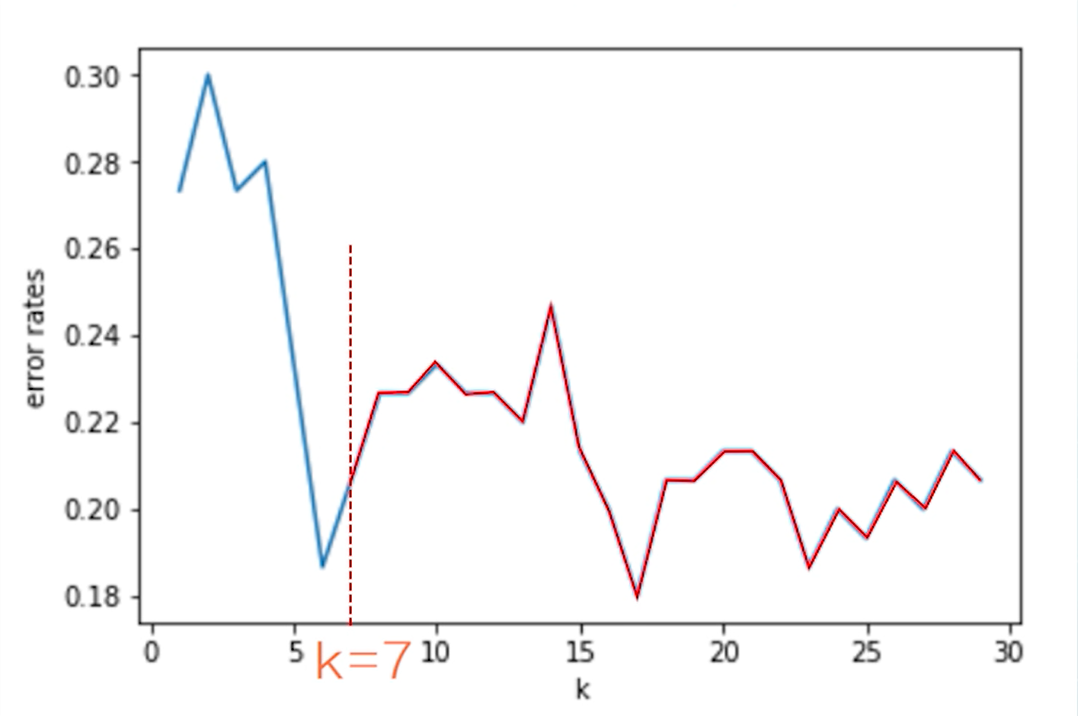
image.png
这个图给了一个很好的提示，可以把关心的指标随着参数变化的情况记录下来，然后就可以寻找最佳参数，例如这个例子中的k=6就是一个合适的选择，这其实就是调参过程的核心思想。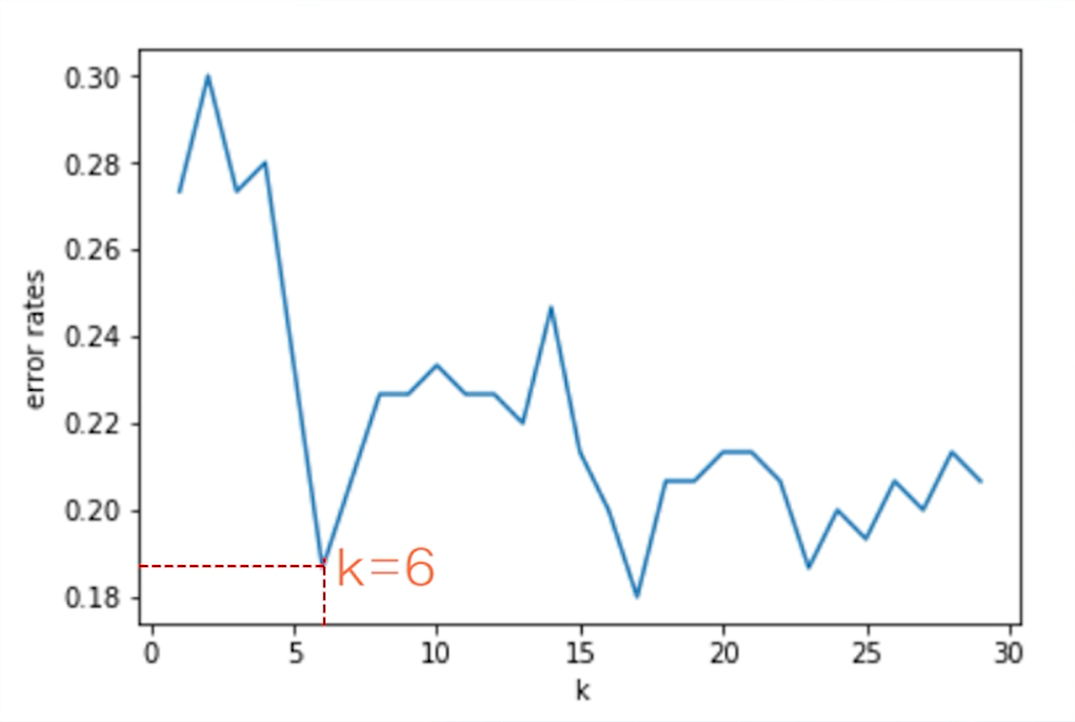
image.png
除了自己构建for循环来实现参数遍历搜索，sklearn库的model_selection模块中还有现成的网格搜索函数——GridSearchCV函数。

参数的网格搜索

sklearn库的model_selection模块中现成的网格搜索函数——GridSearchCV函数。

  1. from sklearn.neighbors import KNeighborsClassifier
  2. from sklearn.model_selection import GridSearchCV
  3. knn=KNeighborsClassifier()
  4. k_range=range(1,30)
  5. param_grid=dict(n_neighbors=k_range)
  6. # cv参数指定了交叉验证的折数，scoring参数指定了评价模型的指标
  7. grid=GridSearchCV(knn,param_grid,cv=5,scoring='accuracy')
  8. # 调用fit方法就可以完成网格参数
  9. grid.fit(my_data[['sepal_length','sepal_width']],my_class)
  10. # 通过grid.cv_results_属性来了解网格搜索建模的具体情况
  11. pd.DataFrame(grid.cv_results_).head(29)

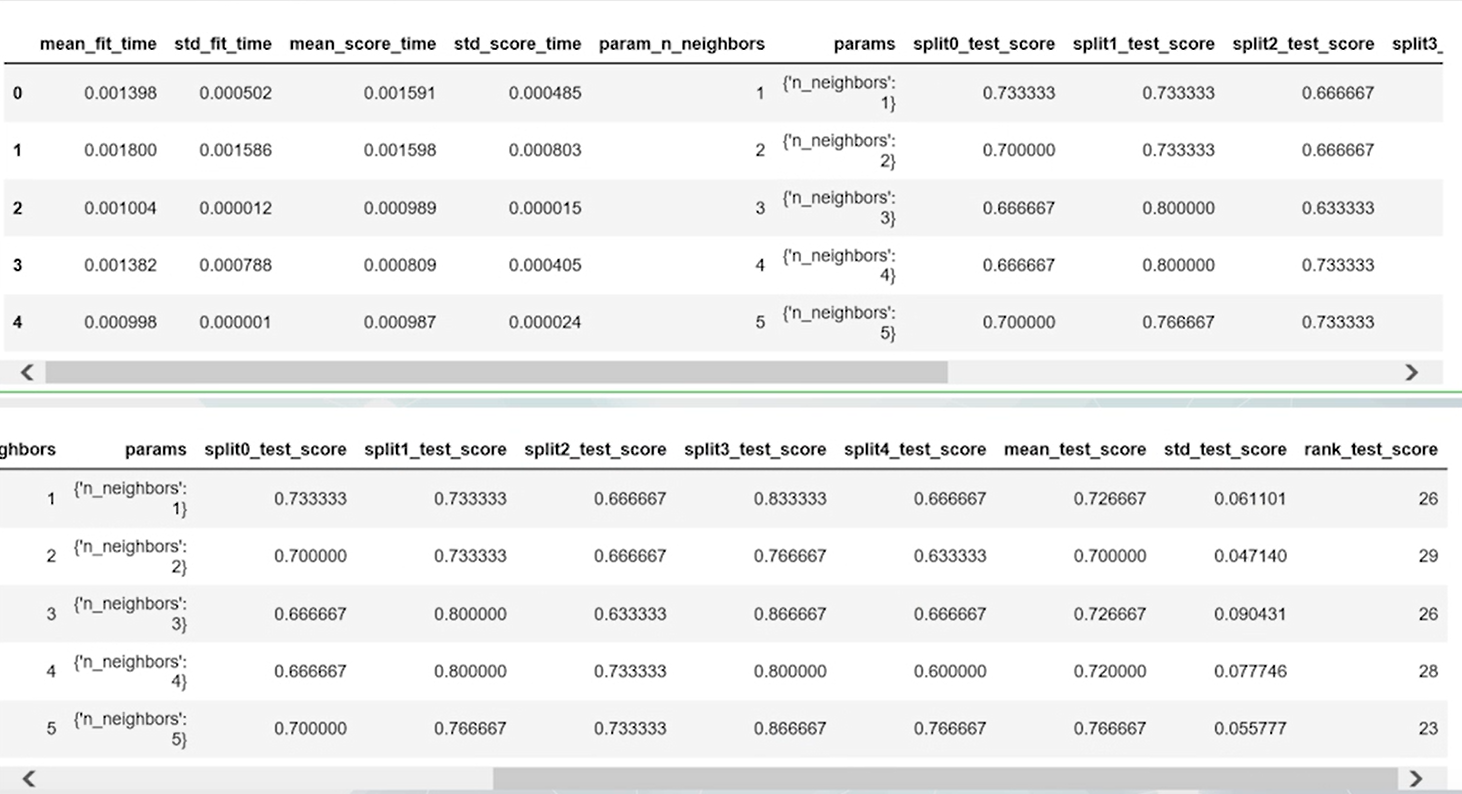
image.png

  1. grid_mean_scores= grid.cv_results_['mean_test_score']
  2. print(grid_mean_scores,'\n')
  3. plt.figure()
  4. plt.xlabel('Tuning Parameter: N nearest neighbors')
  5. plt.ylabel('Classification Accuracy')
  6. plt.plot(k_range,grid_mean_scores)
  7. print('最高得分是近邻值取 k =',grid.best_params_['n_neighbors'],'时的得分,grid.best_score_)
  8. plt.plot(grid.best_params_['n_neighbors'],grid.best_score_,'ro',
  9. markersize=12,markeredgewidth=1.5,
  10. markerfacecolor='None',markeredgecolor='r')

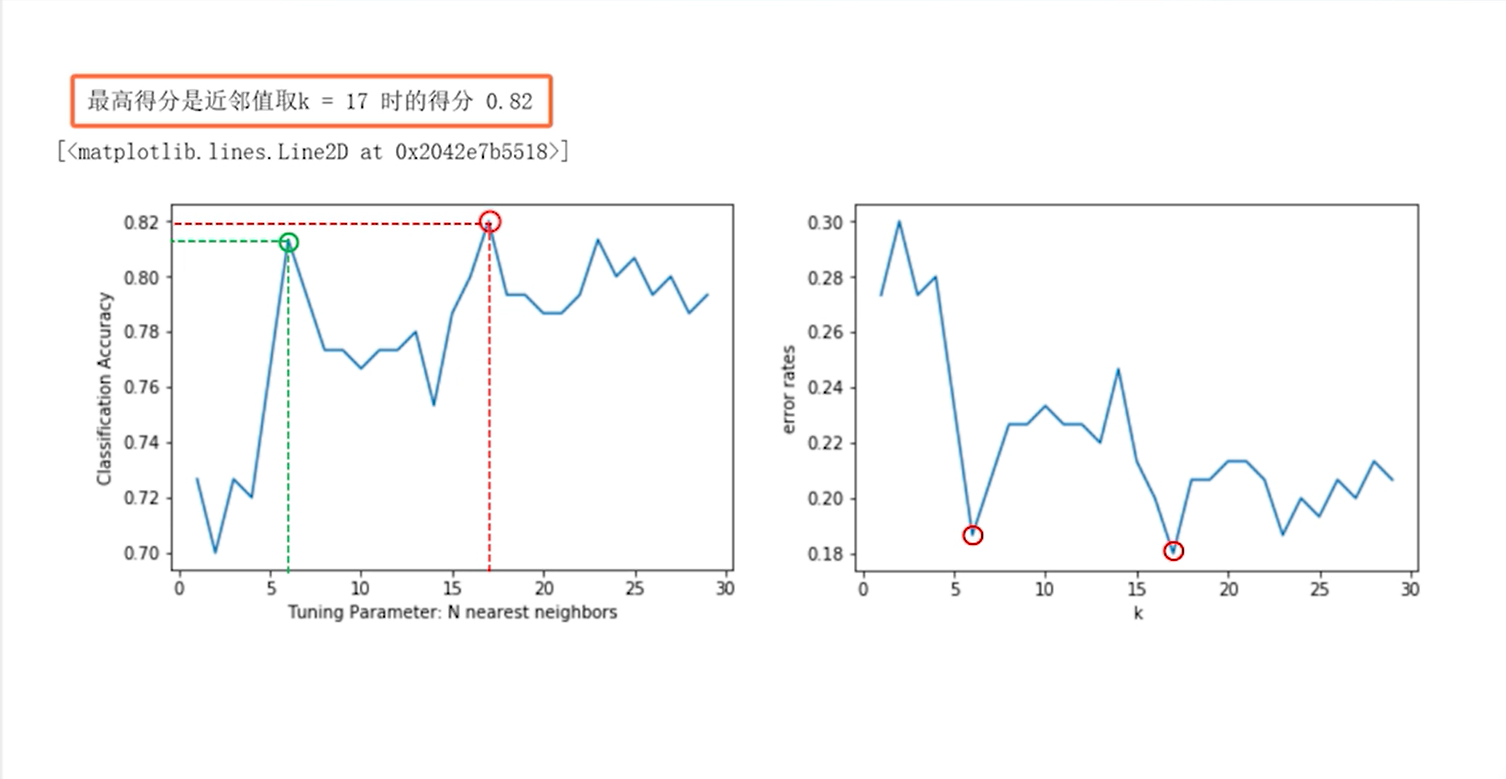
image.png
这里需要说明的是，程序自动找的最佳参数是17，而并非之前选择的k=6，这是因为GridSearchCV只考虑了score的大小，k取17时准确率确实是高于k取6的，这与自己使用for循环搜索的结果是一致的，但是考虑到k取17时处于震荡区，所以这里推荐取6。

  1. print(grid.best_params_)
  2. print(grid.best_score_)
  3. print(grid.best_estimator_)
  4. #p=2 欧氏距离，weights='uniform' 或者'distance'(反距离加权)

image.png
在实际应用中，一般也会结合折现趋势做选择，另外在一些计算机资源消耗密切相关的参数选择，还要考虑到提供性能得分的资源代价。如果性能只是略微提升而时间消耗却大大增加时，一般也会放弃那个绝对性得分最高的选择，而采用得分与资源消耗的综合最优选择。所以现有的库提供了很多自动化的计算，但是真正的选择还是要结合实际情况进行选择。
来实验一下对多个参数进行网格搜索：

多参数网格参数搜索

  1. knn=KNeighborsClassifier()
  2. k_range=range(1,30)
  3. # 算法设置两种选择kd_tree-多维树和ball_tree-超球体树
  4. algorithm_opt=['kd_tree','ball_tree']
  5. # 度量阶数设置从1-5
  6. p_range=range(1,5)
  7. # 加权方式设置两种选择，uniform-均匀加权和distance-反距离加权
  8. weight_range=['uniform','distance']
  9. param_grid=dict(n_neighbors=k_range,weights=weight_range,algorithm=algorithm_opt,p=p_range)
  10. print(param_grid)

image.png
打印参数的字典结构发现确实和设置的一样

  1. # 调用GridSearchCV函数生成示例并初始化
  2. grid=GridSearchCV(knn,param_grid,cv=5,scoring='accuracy')
  3. # 调用fit方法对模型进行拟合和校验
  4. grid.fit(my_data[['sepal_length','sepal_width']],my_class)
  5. # 打印最佳性能得分
  6. print(grid.best_score_)
  7. # 打印最优参数
  8. print(grid.best_estimator_)

image.png
最后可以看到，近邻点数依然选择17，最优算法是’kd_tree’，距离用’minkowski’度量，最优基数为2，均匀加权更好。
模型调参：

  • 模型的数学本质
  • 专业领域
  • 数据科学家的个人经验

    集成学习

    将多个模型进行组合，以期获得比任何一个单独的模型都更好的性能。
    先来看一下模拟模型的例子
    均匀分布：指生成的随机数落在某个区间的概率，与落入其他任何一个同样宽度区间的概率是一样的。例如下面落入0.1到0.2区间和落入0.5到0.6区间的概率是一样的。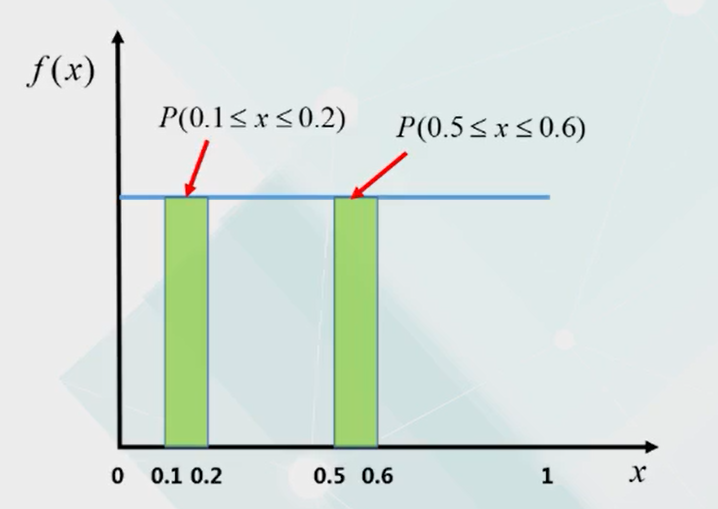
    image.png
    那么当样本容量足够大时，落入某个区间的样本个数就只和区间的宽度和数据值域的占比有关，比如

大于0.1小于0.2的样本个数应该大致占数据总量的0.1/1也就是十分之一。

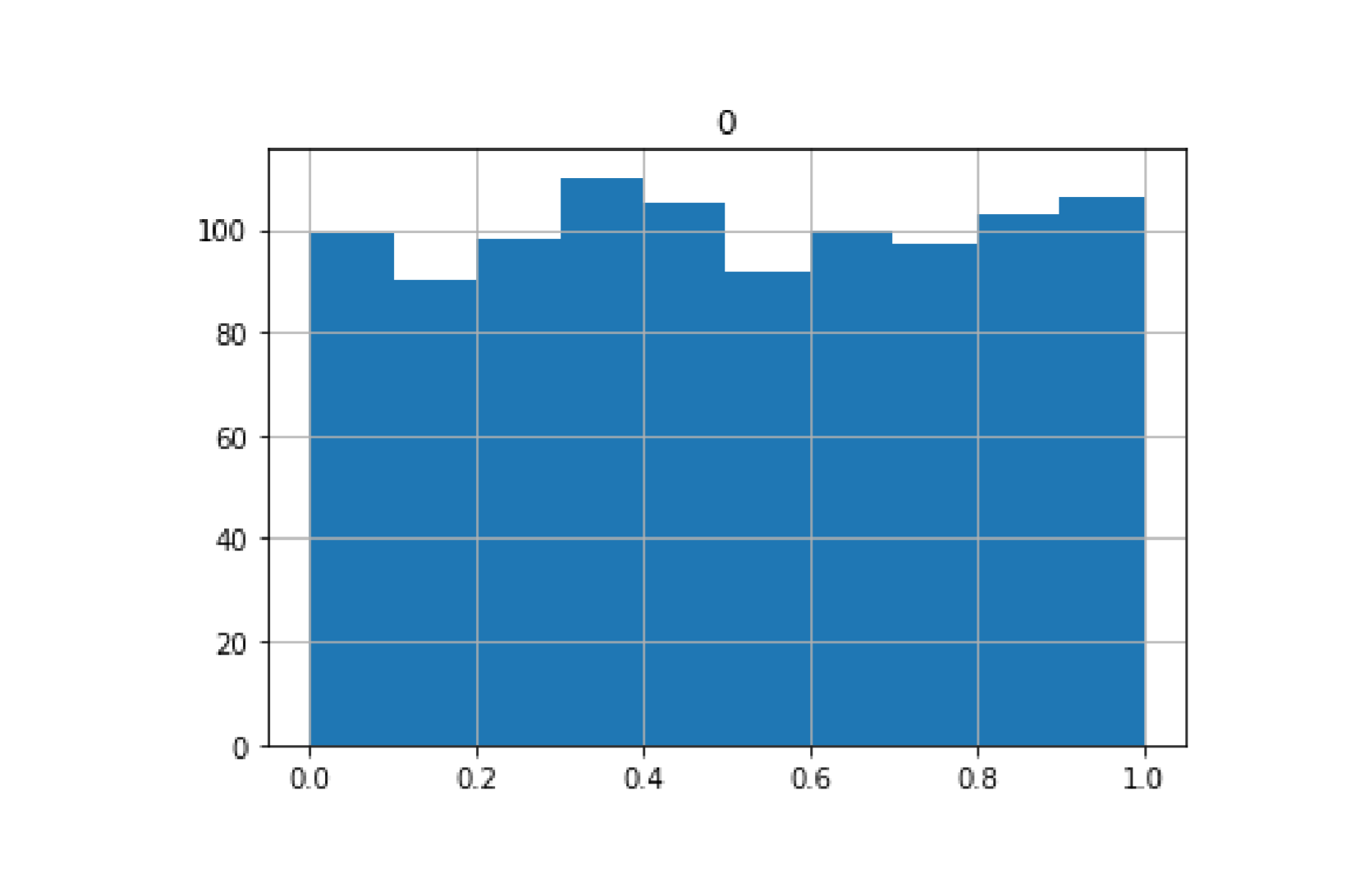
  1. import numpy as np
  2. import pandas as pd
  3. data1=np.random.rand(1000) #[0,1] 均匀分布的随机数
  4. data2=np.random.rand(1000)
  5. data3=np.random.rand(1000)
  6. data4=np.random.rand(1000)
  7. data5=np.random.rand(1000)
  8. pd.DataFrame(data1).hist(bins=10)
  9. print('data1 的 1000 个数中，有',(data1>0.5).sum(),'个数据是大于 0.5 的')
  10. print('data1 的 1000 个数中，有',(data1>0.3).sum(),'个数据是大于 0.3 的')

image.png
image.png

  1. # 大于 0.3 就预测 1，否则预测 0, 假设真实值全 1，则预测的 accuracy=0.7
  2. model1=np.where(data1>0.3,1,0)
  3. model2=np.where(data2>0.3,1,0)
  4. model3=np.where(data3>0.3,1,0)
  5. model4=np.where(data4>0.3,1,0)
  6. model5=np.where(data5>0.3,1,0)
  7. # 均值数学上相当于预测 1 占所有样本的比例，相当于预测的 accuracy
  8. print('第一个模型的 accuracy 是：',model1.mean())
  9. print('第二个模型的 accuracy 是：',model2.mean())
  10. print('第三个模型的 accuracy 是：',model3.mean())
  11. print('第四个模型的 accuracy 是：',model4.mean())
  12. print('第五个模型的 accuracy 是：',model5.mean())

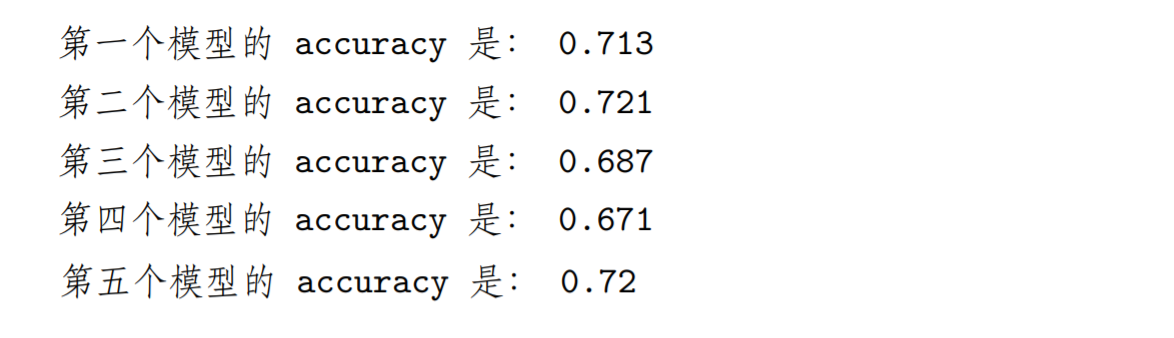
image.png
看到结果显示，五个独立模型的准确率确实都在百分之七十左右。
接下来模拟集成

  1. # 相当于 5 个预测模型累加平均
  2. ensemble_preds=np.round((model1+model2+model3+model4+model5)/5.0).astype(int)
  3. print('集成模型的 accuracy 是：',ensemble_preds.mean())

image.png
此时的准确率约百分之八十四，明显高出原来五个模型的百分之七十，这就是孔多塞陪审团定理，群体的智慧也就是集成，能够提高判断的准确率。
修改模型的参数使得准确率小于百分之五十的时候再来看一下他们的集成结果

  1. # 大于 0.3 就预测 1，否则预测 0, 假设真实值全 1，则预测的 accuracy=0.7
  2. model1=np.where(data1>0.7,1,0)
  3. model2=np.where(data2>0.7,1,0)
  4. model3=np.where(data3>0.7,1,0)
  5. model4=np.where(data4>0.7,1,0)
  6. model5=np.where(data5>0.7,1,0)
  7. # 均值数学上相当于预测 1 占所有样本的比例，相当于预测的 accuracy
  8. print('第一个模型的 accuracy 是：',model1.mean())
  9. print('第二个模型的 accuracy 是：',model2.mean())
  10. print('第三个模型的 accuracy 是：',model3.mean())
  11. print('第四个模型的 accuracy 是：',model4.mean())
  12. print('第五个模型的 accuracy 是：',model5.mean())
  13. # 相当于 5 个预测模型累加平均
  14. ensemble_preds=np.round((model1+model2+model3+model4+model5)/5.0).astype(int)
  15. print('集成模型的 accuracy 是：',ensemble_preds.mean())

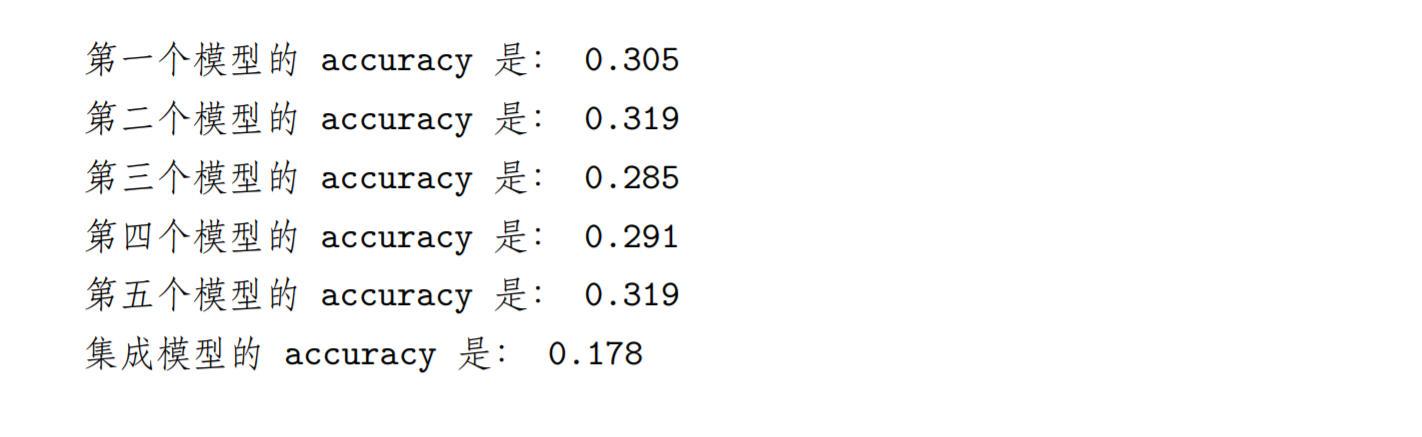
image.png
可以发现集成后性能变得更低了，只有不到百分之十八。如果单个模型有好有坏呢？

  1. # 大于 0.3 就预测 1，否则预测 0, 假设真实值全 1，则预测的 accuracy=0.7
  2. model1=np.where(data1>0.7,1,0)
  3. model2=np.where(data2>0.3,1,0)
  4. model3=np.where(data3>0.6,1,0)
  5. model4=np.where(data4>0.2,1,0)
  6. model5=np.where(data5>0.5,1,0)
  7. # 均值数学上相当于预测 1 占所有样本的比例，相当于预测的 accuracy
  8. print('第一个模型的 accuracy 是：',model1.mean())
  9. print('第二个模型的 accuracy 是：',model2.mean())
  10. print('第三个模型的 accuracy 是：',model3.mean())
  11. print('第四个模型的 accuracy 是：',model4.mean())
  12. print('第五个模型的 accuracy 是：',model5.mean())
  13. # 相当于 5 个预测模型累加平均
  14. ensemble_preds=np.round((model1+model2+model3+model4+model5)/5.0).astype(int)
  15. print('集成模型的 accuracy 是：',ensemble_preds.mean())

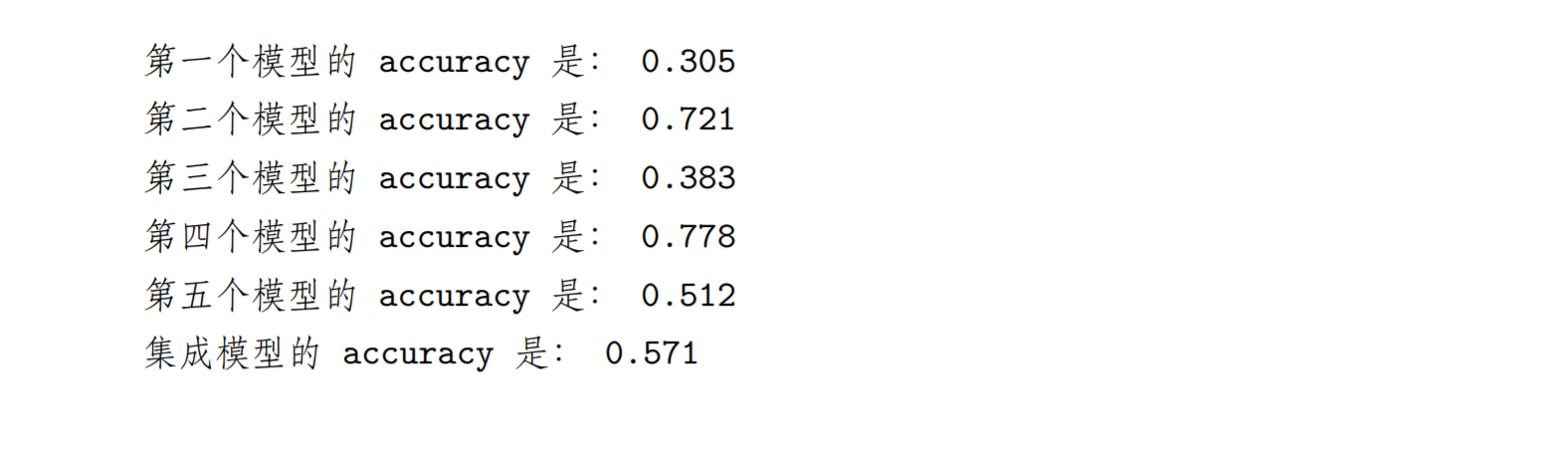
image.png
可以发现集成性能比差的好，比好的差，相当于取了好与坏的折中。

孔多塞陪审团定理前提条件

模型间相互独立（不受其他模型结果影响)
>每个单独的模型必须优于随机模型

决策树的集成

决策树：用带条件判断的二叉树来对数据分组，如果不限定最大树深度，每个分支可以穷尽所有的特征。
在特征足够多的应用中容易造成过拟合，解决的办法有两个：

>Bagging (bootstrap aggregation)

bootstrap：是一种在原始数据集上允许放回的随机抽样操作。
Bootstrap案例
原始数据集
1、2、3、4、5、6、7、8、9、10
Bootstrap sample
2、3、2、8、10、6、5、6、2、9
Step1：从原始训练集中做N次与原始样本容量相等的Bootstrap sarmple;【Bootstrap样本数=原始样本数】
Step2：在以上样本基础上构建N个独立的决策树;【N要足够大、深度足够以保证低偏差】
Step3：综合多次决策树的结果;
分类问题——投票
回归问题——平均

>随机森林

构建决策树时，从全体p个特征中随机挑选m个。
区别：对特征进行随机挑选
构造步骤：
Step1：对特征进行N次独立随机挑选，每次挑选不少于一定量的特征作为单棵决策树的候选特征;
Step2：基于每个候选特征集合独立构造一棵决策树;
Step3：N棵决策树的结果投票或平均形成集成的输出。
使用德国银行的信用数据建一个随机森林模型，这个文件包含一千个用户数据，20个特征，一个用户类型标签，标签显示有300个用户是高风险用户，特征中既有数值型数据，又有很多类别数据，先对类别数据作编码。
利用sklearn库中ensemble模块的RandomForestClassifier对象可以构造随机森林模型。
然后使用sklearn.model_selection模块中的cross_val_score函数进行交叉验证并评价模型。 ```python

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import cross_val_score from sklearn.ensemble import RandomForestClassifier feature_col=my_data.columns X=my_data[[‘duration’]] # for n,my_str in enumerate(feature_col): if (my_str!=’customer_type’) & (my_str != ‘duration’): if my_data[[my_str]].dtypes[0]!=object: X=pd.concat([X,my_data[[my_str]]],axis=1) for n,my_str in enumerate(feature_col): if my_data[[my_str]].dtypes[0] == object: my_dummy=pd.get_dummies(my_data[[my_str]],prefix=my_str) X=pd.concat([X,my_dummy],axis=1) print(X.info())

  1. 由于1000个中只有300个是高风险，两种类别不平衡，所以采用ROC曲线的AUC参数为性能的评估参数。
  2. ```python
  3. estimator_range=range(10,400,10)
  4. my_scores=[]
  5. for estimator in estimator_range:
  6.     my_tree=RandomForestClassifier(n_estimators=estimator)
  7.     accuracy_scores=cross_val_score(my_tree,X,my_data['customer_type'],cv=5,scoring='roc_auc')
  8.     my_scores.append(accuracy_scores.mean())
  9. plt.plot(estimator_range,my_scores)
  10. plt.xlabel('the number of trees')
  11. plt.ylabel('ROC_AUC')

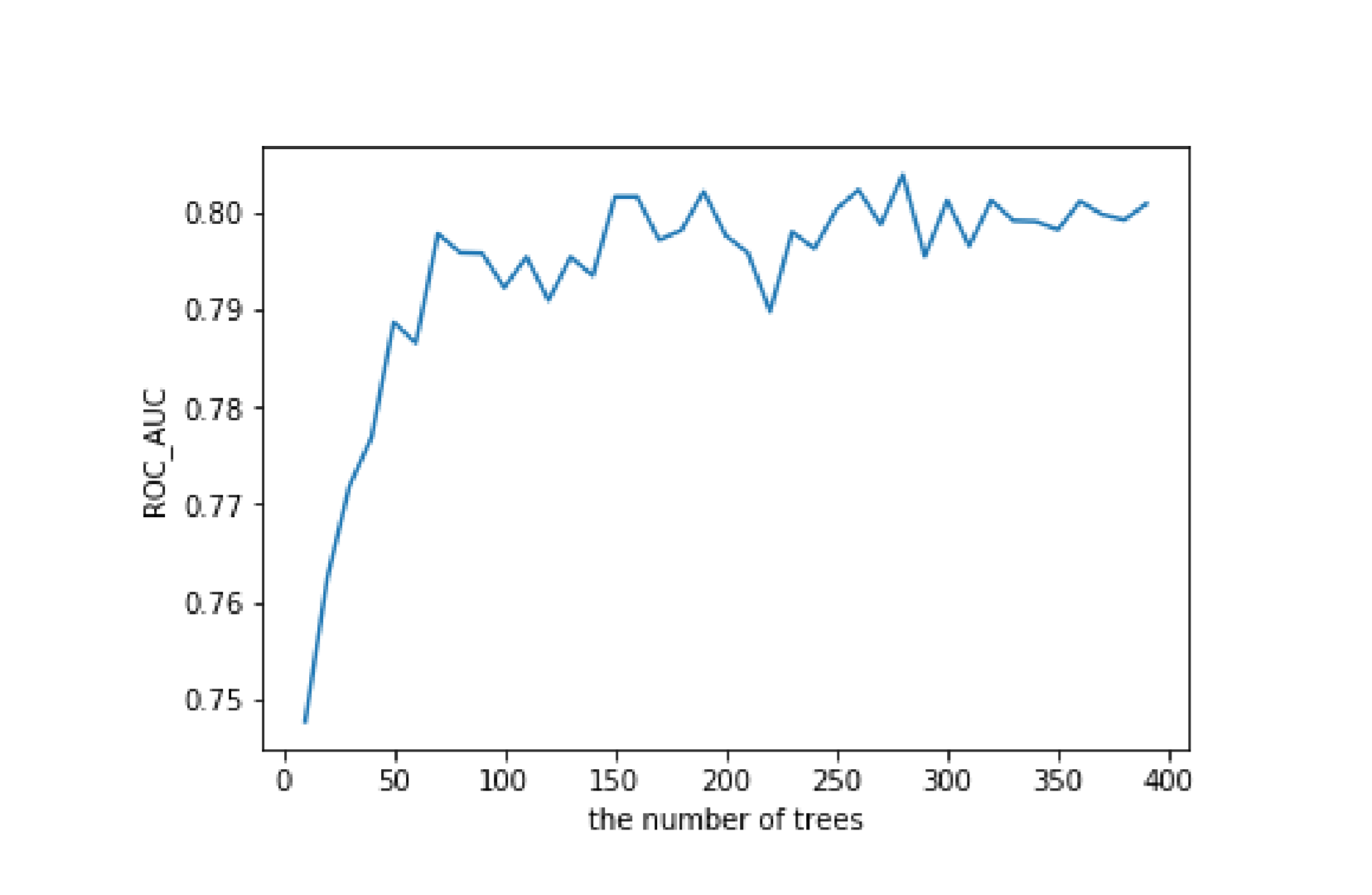
image.png
从结果图可以看出，树的个数超过150以后，分类集的性能开始趋于平稳。
最后还可以使用RandomForestClassifier对象中的feature_importances_属性看一下特征在分类中的重要性。然后通过sort_values方法进行排序输出。

  1. my_RF=RandomForestClassifier(n_estimators=150)
  2. my_RF.fit(X,my_data['customer_type'])
  3. pd.DataFrame({'feature':X.columns,'importance':my_RF.feature_importances_}).sort_values('importance',ascending=False)

image.png
从结果可以看出当前欠款金额是最重要的特征。
随机森林是应用最广泛的模型之一，由于集成的优势，他的性能与其他优秀的模型比起来都不会差太多，同时随机森林由于本身就有对特征和数据的重抽样，因此哪怕不特别进行训练集和测试集划分或交叉验证，其性能指标也是比较可靠的。此外，集成的做法使得特征的重要性也更可靠。
但是由于是多个数的并行结构，随机森林训练和预测起来都比较慢，而且难以像决策树那样可视化。
优势：集成———性能有保证、性能评价和特征重要性可靠
劣势：训练和预测比较慢