图神经网络

神经网络

一、图神经网络介绍

**

图神经网络(Graph Neural Networks, GNNs)是基于图结构的深度学习方法，近期被广泛应用到各类图像、自然语言处理等任务上。图神经网络作为神经网络扩展，可以处理以图结构表示的数据格式。在图中，每个节点都由本身的特性以及其相邻的节点和关系所定义，网络通过递归地聚合和转换相邻节点的表示向量来计算节点的表示向量。
在论文《Relational inductive biases, deep learning, and graph networks》中，作者定义了通用图网络框架graph networks (GN) framework，概括和扩展了各种图神经网络，并且支持使用简单的模块来构建复杂的结构。GN framework的主要计算单元是GN block，一个图到图的模块，它的输入是一个图，在图结构上进行计算，然后得到同样是图结构的输出。
在GN framework下，一个图可以被定义为一个三元组，是图的一个全局表示， 代表图中个节点的集合，为节点i的表示，表示图中条边的集合，为边的表示，和分别代表边的接收节点和发送节点。
每一个GN block包含三个更新函数，以及三个聚合函数：



上式中，，。
其中 应用于图中每条边的更新， 应用于图中每个节点的更新， 则用来更新图的全局表示；函数将输入的表示集合整合为一个表示，该函数设计为可以接收任意大小的集合输入，通常可以为加和、平均值或者最大值等不限输入个数的操作。
当一个GN block得到一个图 的输入时，计算通常从边到节点，再到全局进行。下图给出了一个GN block的更新过程。

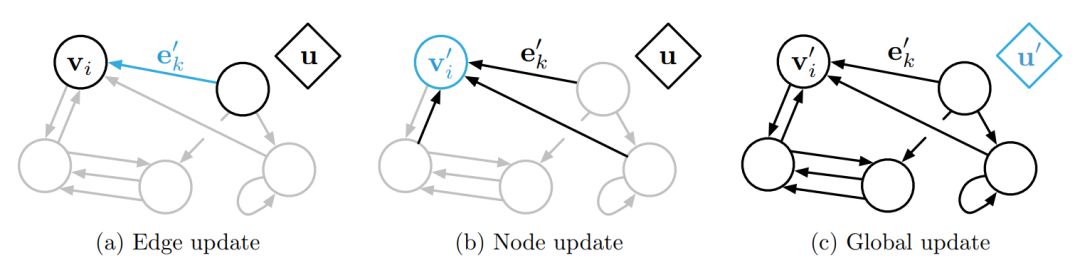
图1 一个GN block的更新过程
一个GN block的计算可以被描述为如下几步：
1. 更新每一条边，输入参数为边表示，接收和发送节点的表示和以及全局表示，输出为更新过的边表示；
2. 用来有同一个聚合接收节点的边的信息，对节点i得到所有入边及邻近节点信息整合，用于下一步节点的更新；
3. 更新每一个节点，输入为上文中的，节点表示$以及全局表示，输出为更新过的节点表示；
4. 聚合图中所有边的信息得到边信息整合；
5. 通过聚合图中所有节点信息得到节点的信息整合；
6. 更新全局的表示，输入为边信息整合，节点信息整合，以及节点表示，输出为更新过的全局表示 。
可以通过上述的更新步骤来套用目前的图神经网络算法，当然这里的步骤的顺序并不是严格固定的，比如可以先更新全局信息，再更新节点信息以及边的信息。

为什么要使用图神经网络

图神经网络有灵活的结构和更新方式，可以很好的表达一些数据本身的结构特性，除了一些自带图结构的数据集（如Cora，Citeseer等）以外，图神经网络目前也被应用在更多的任务上，比如文本摘要，文本分类和序列标注任务等，目前图神经网络以及其变种在很多任务上都取得了目前最好的结果。
比较常见的图神经网络算法主要有Graph Convolutional Network（GCN）和Graph Attention Network（GAT）等网络及其变种，在本文第三部分会给出基于图神经网络框架DGL的GCN以及GAT的代码及注解。

二、图神经网络库

相比于传统的基于邻接矩阵的图神经网络实现方法，目前完成度较好的图神经网络框架主要是基于PyTorch和MXNet的DGL (Deep Graph Library)和PyG (PyTorch Geometric)。主要使用DGL作为开发的框架，原因是各种网络模型的tutorial给的比较详尽，同时包括TreeLSTM这种经典模型也可以通过给定节点访问的顺序通过框架很轻松的实现，相比于不使用图网络框架的代码具有更强的可读性。
但是，实际上图神经网络框架只适用于图结构中的边和点是同一量级的情况，因为图神经网络框架的信息是通过图中的边来传递的，会将节点的表示复制多次。在这种情况下，反而不如使用邻接矩阵直接做矩阵乘法，因为使用邻接矩阵做矩阵乘法其实不会将节点信息复制多次，会对显存有极大的节省。

三、常见算法以及代码示例详解

GCN

GCN的计算公式如下：
上式中表示网络的第l层，代表非线性激活函数，为该层的权重矩阵，和分别代表度矩阵以及邻接矩阵，~符号表示对每一个节点加上一个自环，即，为单位矩阵，由于邻接矩阵是没有进行正则化的，所以论文中通过使得结果中每一行的和都为1。

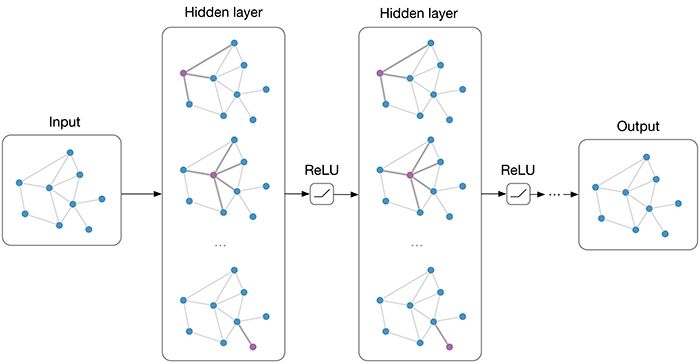
图2 在每一层图网络中，每个节点通过对邻近节点的信息聚合得到这层该节点的输出
相比于前文给出的GCN基于邻接矩阵的公式定义，GCN的公式可以被更简洁的定义为以下两步：
1）对于节点u,首先将节点邻居表示聚合到一起，生成中间表示，
2）将得到的中间表示通过一层非线性神经网络层。
下面为基于DGL的代码示例，在代码实现中，第一步通过DGL自带的message passing函数实现，第二步通过DGL的apply_nodes方法，将基于PyTorch中nn.Module的用户自定义函数加入实现：

import dgl
import dgl.function as fn
import torch as th
import torch.nn as nn
import torch.nn.functional as F
from dgl import DGLGraph
gcn_msg = fn.copy_src(src='h', out='m')
gcn_reduce = fn.sum(msg='m', out='h')

接下来为apply_nodes定义更新节点的自定义函数，这里是一个线性变换加上一个非线性激活函数的网络层：

class NodeApplyModule(nn.Module):
    def __init__(self, in_feats, out_feats, activation):
        super(NodeApplyModule, self).__init__()
        self.linear = nn.Linear(in_feats, out_feats)
        self.activation = activation
    def forward(self, node):
        h = self.linear(node.data['h'])
        h = self.activation(h)
        return {'h' : h}

下面定义GCN模块，一层GCN首先通过update_all方法将节点信息通过边传递，然后通过apply_nodes得到新的节点表示：

class GCN(nn.Module):
    def __init__(self, in_feats, out_feats, activation):
        super(GCN, self).__init__()
        self.apply_mod = NodeApplyModule(in_feats, out_feats, activation)
    def forward(self, g, feature):
        g.ndata['h'] = feature
        g.update_all(gcn_msg, gcn_reduce)
        g.apply_nodes(func=self.apply_mod)
        return g.ndata.pop('h')

整个网络模块的定义和Pytorch中的NN模型定义本质上相同，如下我们定义两个GCN网络层：

class Net(nn.Module):
    def __init__(self, in_dim, hidden_dim, out_dim):
        super(Net, self).__init__()
        self.gcn1 = GCN(in_dim, hidden_dim, F.relu)
        self.gcn2 = GCN(hidden_dim, out_dim, F.relu)
        def forward(self, g, features):
            x = self.gcn1(g, features)
            x = self.gcn2(g, x)
            return x
        net = Net()
        print(net)

GAT

GAT和GCN的主要区别就在于邻近节点信息的聚合方式，GAT通过引入attention机制来替代GCN中的静态归一化卷积运算，下面给出使用 l 层网络输出来计算第 l+1 层网络输出的公式：





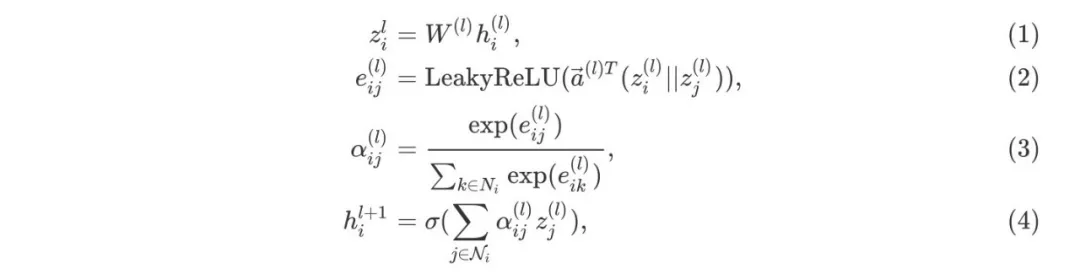
在上式中，公式(1)为上一层节点表示通过可学习的权重矩阵做线性变换；公式(2)计算两个邻近节点的为未进行标准化的attention分数，这里首先将两个节点的表示相连，然后和一个可学习的权重向量做点积，最后通过函数。这种形式通常叫做additive attention，相比Transformer中的则是dot-product attention；公式(3)对每个与该节点有入边的节点的attention分数使用softmax函数作归一化操作；公式(4)与GCN类似，聚合邻近节点的表示，使用公式(3)得到的分数作为权值。具体的计算方式如下图所示：

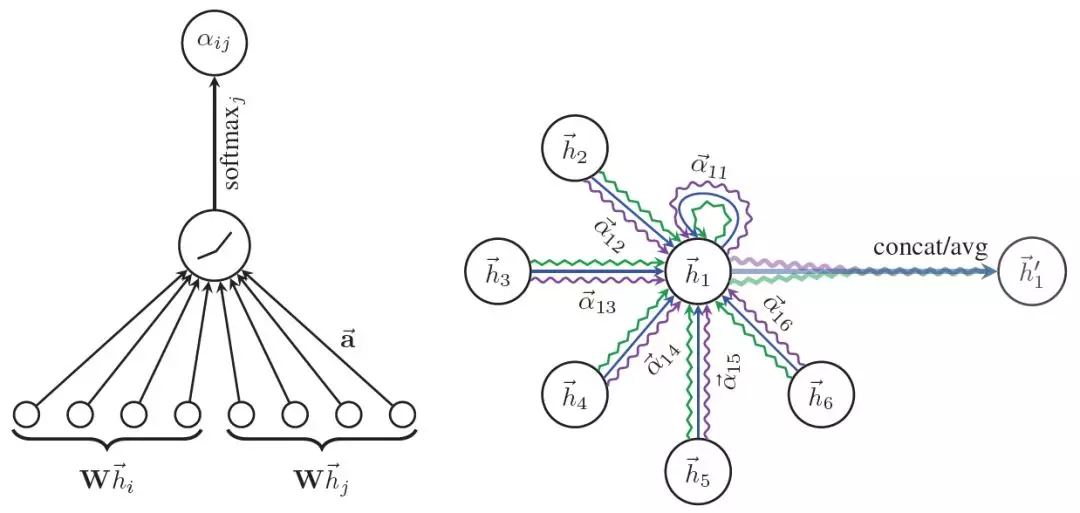
图3 Graph Attention Networks计算attention分数以及更新节点表示
下面的基于DGL的代码逐一分解了上面的四个公式，公式(1)中的线性变换直接使用Pytorch中的torch.nn.Linear模块

import torch
import torch.nn as nn
import torch.nn.functional as F
class GATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim):
        super(GATLayer, self).__init__()
        self.g = g
        # equation (1)
        self.fc = nn.Linear(in_dim, out_dim, bias=False)
        # equation (2)
        self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False)
    def edge_attention(self, edges):
        # edge UDF for equation (2)
        z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)
        a = self.attn_fc(z2)
        return {'e': F.leaky_relu(a)}
    def message_func(self, edges):
        # message UDF for equation (3) & (4)
        return {'z': edges.src['z'], 'e': edges.data['e']}
    def reduce_func(self, nodes):
        # reduce UDF for equation (3) & (4)
        # equation (3)
        alpha = F.softmax(nodes.mailbox['e'], dim=1)
        # equation (4)
        h = torch.sum(alpha * nodes.mailbox['z'], dim=1)
        return {'h': h}
    def forward(self, h):
        # equation (1)
        z = self.fc(h)
        self.g.ndata['z'] = z
        # equation (2)
        self.g.apply_edges(self.edge_attention)
        # equation (3) & (4)
        self.g.update_all(self.message_func, self.reduce_func)
        return self.g.ndata.pop('h')

公式(2)中的通过两个相邻节点i和j的表示计算，这里通过DGL的apply_edgesAPI来实现，参数是下面的自定义函数edge_attention：

1def edge_attention(self, edges):
2    # edge UDF for equation (2)
3    z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)
4    a = self.attn_fc(z2)
5    return {'e' : F.leaky_relu(a)}

这里和可学习权重向量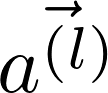的点积通过上面定义的线性变换函数attn_fc得到，这里apply_edge会将所有的边的数据放到一个tensor里，所以cat，attn_fc可以并行计算，这也是上文提到的如果边的数量比点的数量多一个量级，最好还是使用邻接矩阵的方式实现图网络的原因，因为会将点的信息复制多次。
对于公式(3)和公式(4)，使用update_allAPI来实现所有节点的信息传递，message function会发送两部分信息：经过变换的表示和每条边上尚未经过归一化的attention分数，然后通过下面的reduce function，首先通过softmax对attention的分数作归一化操作（公式(3)），然后将节点的邻近节点的表示按照归一化之后的attention权重聚合起来得到新的表示（公式(4)）：

def reduce_func(self, nodes):
    # reduce UDF for equation (3) & (4)
    # equation (3)
    alpha = F.softmax(nodes.mailbox['e'], dim=1)
    # equation (4)
    h = torch.sum(alpha * nodes.mailbox['z'], dim=1)
    return {'h' : h}

GAT同样使用了类似Transformer的Multi-head Attention，用来加强模型表达能力并且稳定学习过程。每一个attention head有自己独立的参数，可以通过两种方式合并它们的输出：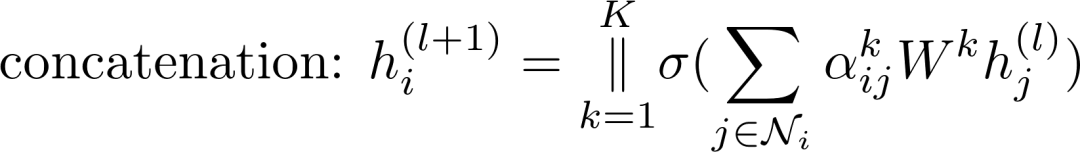
或者average：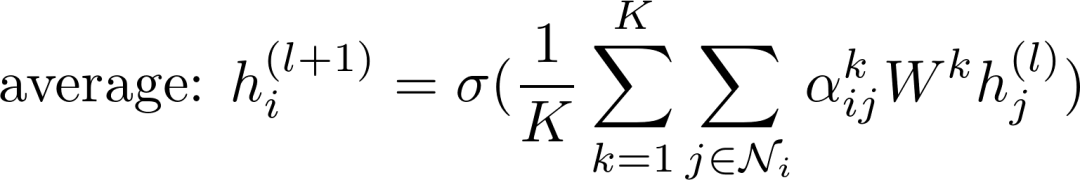
上式中代表attention heads的数量，原作者建议对于网络中间层使用concatenation，最后一层使用average得到attention的输出，与上面的单个head的GATLayer相结合可以得到下面的代码：

class MultiHeadGATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim, num_heads, merge='cat'):
        super(MultiHeadGATLayer, self).__init__()
        self.heads = nn.ModuleList()
        for i in range(num_heads):
            self.heads.append(GATLayer(g, in_dim, out_dim))
        self.merge = merge
    def forward(self, h):
        head_outs = [attn_head(h) for attn_head in self.heads]
        if self.merge == 'cat':
            # concat on the output feature dimension (dim=1)
            return torch.cat(head_outs, dim=1)
        else:
            # merge using average
            return torch.mean(torch.stack(head_outs))

最后定义一个两层的GAT模型

class GAT(nn.Module):
    def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):
        super(GAT, self).__init__()
        self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)
        # Be aware that the input dimension is hidden_dim*num_heads since
        # multiple head outputs are concatenated together. Also, only
        # one attention head in the output layer.
        self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)
    def forward(self, h):
        h = self.layer1(h)
        h = F.elu(h)
        h = self.layer2(h)
        return h

上面GAT和GCN的详细代码可以在DGL的Github(https://github.com/dmlc/dgl)上找到。

四、总结

图神经网络在近期的研究中被广泛应用，结合参考资料和自身对图神经网络的理解，总结了一个快速上手的简要教程。除了在一些有着天然图结构的任务，图神经网络也可以应用在自然语言处理任务中，可以在模型中更好地表示信息。本文还给出了基于图神经网络框架DGL的GCN和GAT的代码及注解，但是根据实际使用经验，图神经网络框架在处理边数量比节点数量多一个量级的情况下，会比使用邻接矩阵的写法占用更多的内存，还是需要根据具体情况来选择使用。