机器学习 Python

问题

如果有一组数据，如何确定他们来自哪个统计分布？
从数据分析的角度，并不想要通过严格的统计方法去找到这个分布，其实 Python 中有一个可以自动拟合数据分布的库 —— distfit 。这是一个python包，用于通过残差平方和（RSS）和拟合优度检验（GOF）对89个单变量分布进行概率密度拟合，并返回最佳分布。

distfit 简单又好用

  1. # 安装
  2. pip install distfit

常见用法：
.fit_transform()：在经验数据 X 上拟合分布
.summary：获得拟合数据并测试拟合优度的所有分布的分数。
.predict()：预测响应变量的概率
.model：输出分布的最佳参数
.plot()：绘制最佳的拟合分布

示例

  1. from distfit import distfit
  2. import numpy as np
  3. X = np.random.normal(0, 2, [100,10])
  4. y = [-8,-6,0,1,2,3,4,5,6]
  5. dist = distfit(todf=True)
  6. dist.fit_transform(X)
  7. dist.plot()

输出用于拟合过程的函数列表，它使用最流行的 10 个发行版的列表进行扫描。

  1. [distfit] >[norm      ] [0.00 sec] [RSS: 0.0120713] [loc=-0.047 scale=1.984]
  2. [distfit] >[expon     ] [0.0 sec] [RSS: 0.4092169] [loc=-7.320 scale=7.273]
  3. [distfit] >[pareto    ] [0.06 sec] [RSS: 0.4098607] [loc=-98251992.546 scale=98251985.226]
  4. [distfit] >[dweibull  ] [0.01 sec] [RSS: 0.0229391] [loc=-0.046 scale=1.721]
  5. [distfit] >[t         ] [0.04 sec] [RSS: 0.0120717] [loc=-0.047 scale=1.984]
  6. [distfit] >[genextreme] [0.05 sec] [RSS: 0.0107445] [loc=-0.755 scale=1.981]
  7. [distfit] >[gamma     ] [0.04 sec] [RSS: 0.0118907] [loc=-191.812 scale=0.021]
  8. [distfit] >[lognorm   ] [0.09 sec] [RSS: 0.0117103] [loc=-107.148 scale=107.084]
  9. [distfit] >[beta      ] [0.03 sec] [RSS: 0.0116300] [loc=-14.479 scale=28.973]
  10. [distfit] >[uniform   ] [0.0 sec] [RSS: 0.2545746] [loc=-7.320 scale=12.835]
  11. [distfit] >[loggamma  ] [0.04 sec] [RSS: 0.0123738] [loc=-360.941 scale=54.518]

当然，distfit 支持的分布还有很多：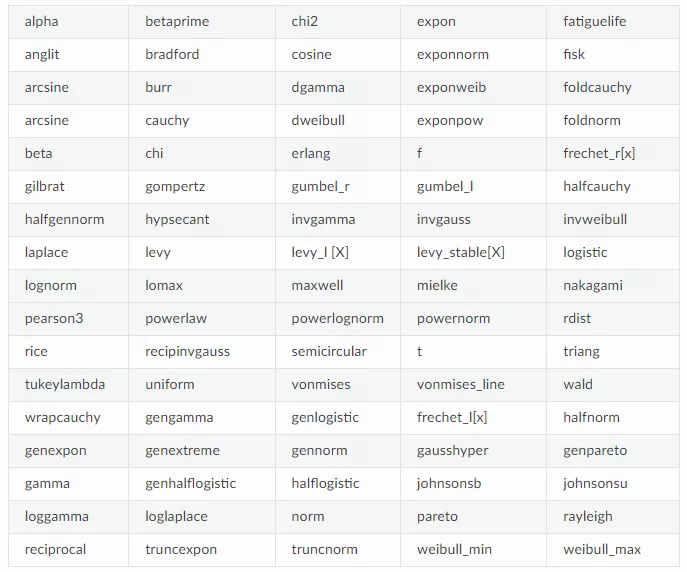
用Python学线性代数：自动拟合数据分布 - 图1
最后绘制最佳的拟合分布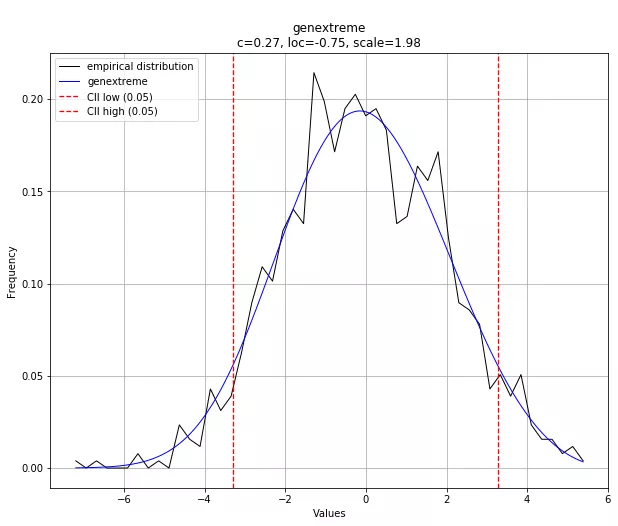用Python学线性代数：自动拟合数据分布 - 图2
dist.summary 输出各分布的参数。

  1.          distr      score  ...       scale                                       arg
  2. 0   genextreme  0.0107445  ...      1.9814                    (0.27387377680364405,)
  3. 1         beta    0.01163  ...     28.9726  (26.055079164665887, 26.248878389403494)
  4. 2      lognorm  0.0117103  ...     107.084                    (0.01848064379707136,)
  5. 3        gamma  0.0118907  ...   0.0205321                      (9339.777394183824,)
  6. 4         norm  0.0120713  ...     1.98429                                        ()
  7. 5            t  0.0120717  ...     1.98428                      (1863131.339823592,)
  8. 6     loggamma  0.0123738  ...     54.5178                      (750.2645425001494,)
  9. 7     dweibull  0.0229391  ...     1.72129                     (1.2898970802235787,)
  10. 8      uniform   0.254575  ...     12.8346                                        ()
  11. 9        expon   0.409217  ...     7.27316                                        ()
  12. 10      pareto   0.409861  ...  9.8252e+07                     (13542571.060345018,)