Ch 6.3 抽样分布

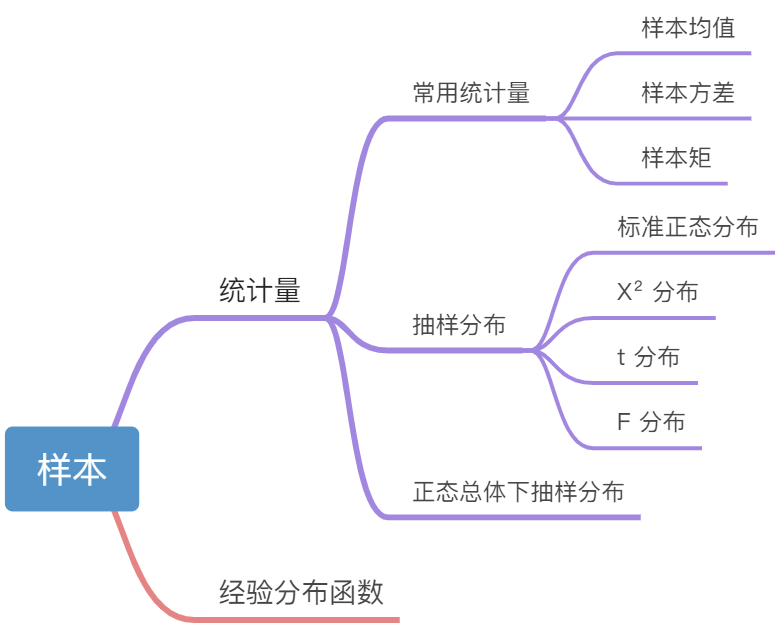
Mindmap

6.3.1 公式汇总

样本平均值：
样本方差： (自由度-1，因此分母为n-1;解释：由均值可以推算最后一个数字，因此已经被限制)
样本标准差：
样本k阶（原点）矩：
样本k阶中心矩

6.3.2 X²分布(卡方分布)

概述

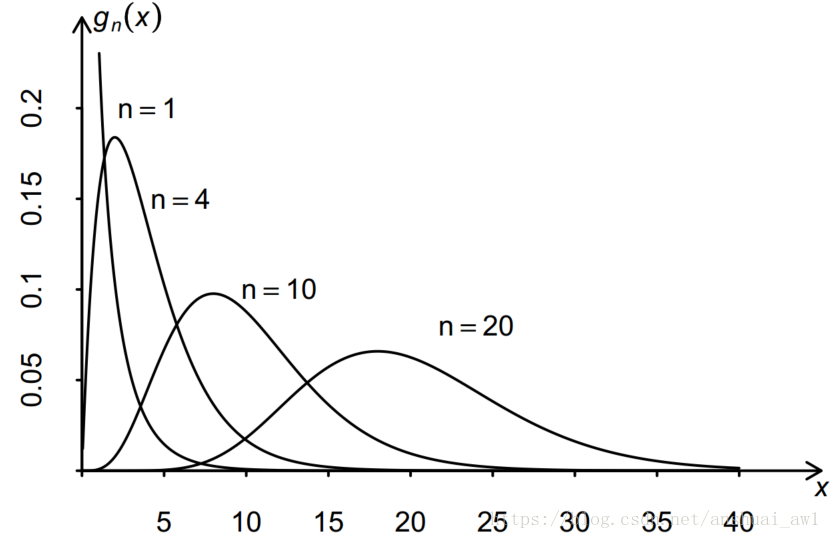在x=n-2时取值最大
设是来自总体的样本，则称统计量

服从自由度为n的
概率密度不要求掌握

性质

X²分布的可加性** 设，并且相互独立，则有
X²分布的数学期望与方差** 若X²~X²(n)，则有

X²分布上分位点

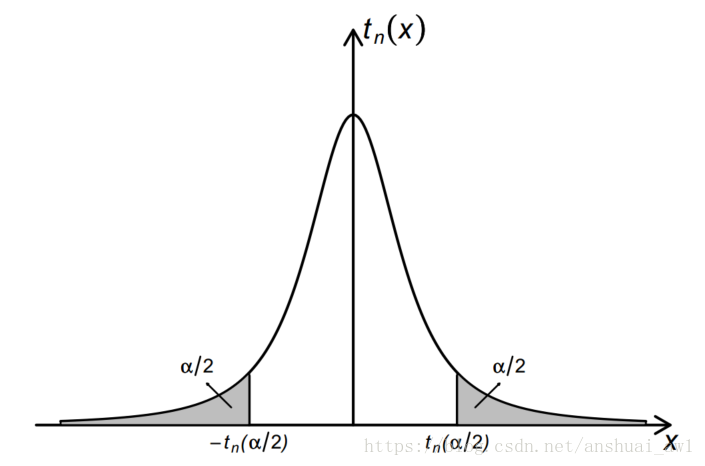
上α分位数：
其中n为定值参数，为X轴上的一个点，而α代表概率（即为面积）

例题

i. 已知服从，求 解： ，服从卡方分布 （查表可得）

6.3.3 t分布

概述

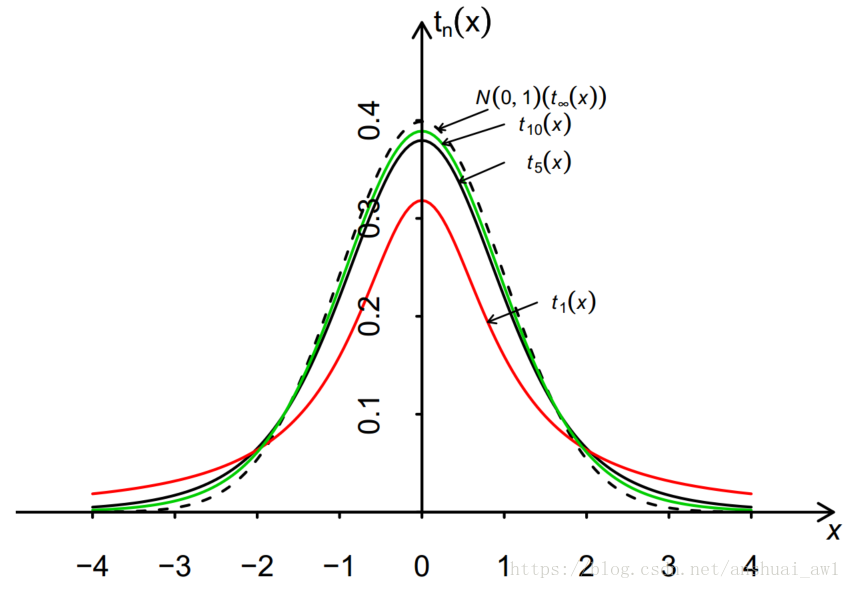（当n充分大时其图形类似于标准正态变量概率密度的图形）
设，且X，Y相互独立，则称随机变量 服从自由度为n的t分布. 记为t~t(n)

概率密度函数不要求掌握

t分布上分位点

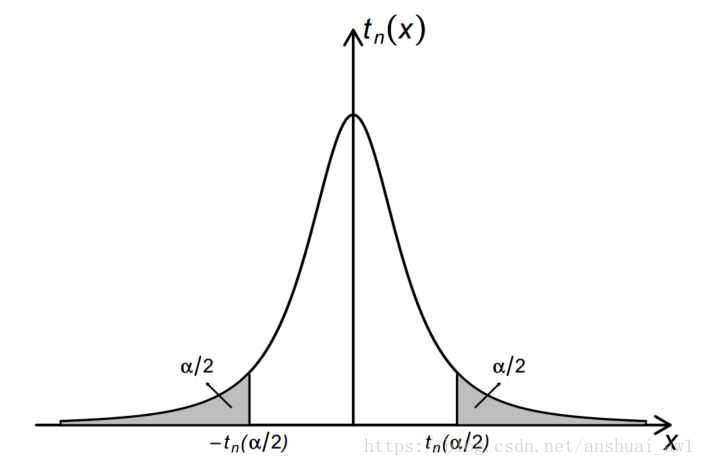
中，α为概率（面积），为X轴上的某一点

例题

i. 已知服从N(0,4) 独立，令求中的 解： 由于t分布 ，求在t(4)中P大于0.005的值

6.3.4 F分布

概述

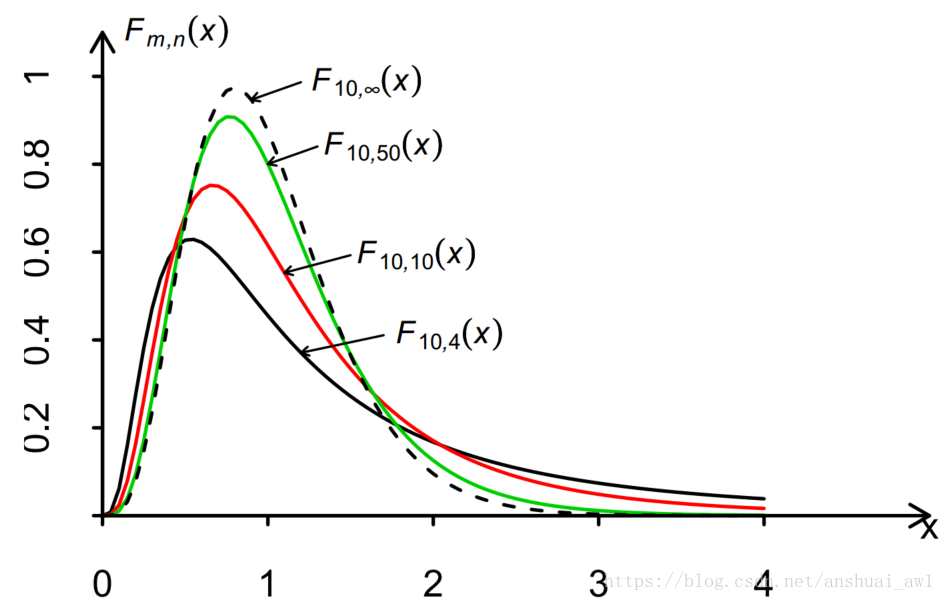
设且U, V相互独立，则称随机变量
服从自由度为的F分布，记为，记为

性质

若则 （换位）