插入排序 Insertion Sort

概念

插入排序是一种简单直观的排序算法。在插入排序中，我们从前到后依次处理未排好序的元素，对于每个元素，我们将它与之前排好序的元素进行比较，找到对应的位置后并插入。本质上，对于每一个要被处理的元素，我们只关心它与之前元素的关系，当前元素之后的元素我们下一轮才去处理。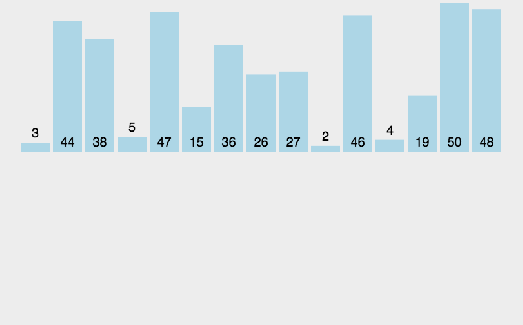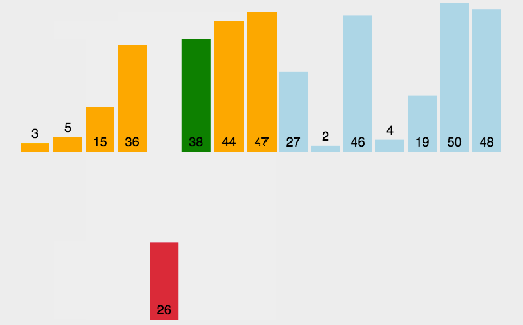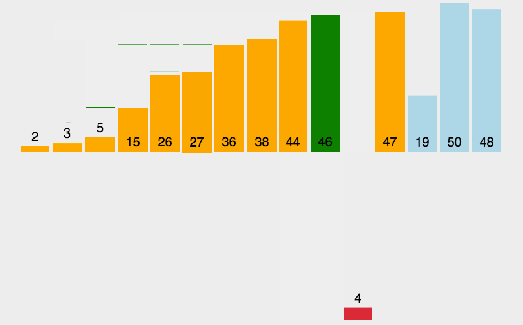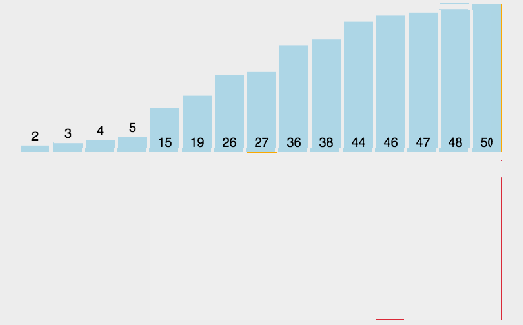

在实现上，每个元素和之前元素比较的过程，是一个从后到前扫描的过程。在扫描时，我们将已排好序的元素先后挪位，为新的元素提供插入位置。这也叫做 in-place 排序，这样我们就不需要额外的内存空间了。

具体步骤

1. 从第二个元素（第一个要被排序的新元素）开始，从后向前扫描之前的元素序列
2. 如果当前扫描的元素大于新元素，将扫描元素移动到下一位
3. 重复步骤2，直到找到一个小于或者等于新元素的位置
4. 将新元素插入到该位置
5. 对于之后的元素重复步骤1~4

复杂度分析

时间复杂度：O(n²)
空间复杂度：O(1)
「时间复杂度」在此算法中就是计算比较的次数，第一个元素我们需要比较1次，第二个元素2次，对于第n个元素，我们需要和之前的元素比较n次，比较总数量也就是 1 + 2 + … + n = n(n + 1) / 2
≈ n^2。因为我们调换位置时采用「原地操作」(in place)，所以不需要额外空间，既空间复杂度为O(1)。

public void insertionSort(int[] array) {
    for(int i = 1; i < array.length; i++) {
        int cur = array[i];
        int insertionIndex = i - 1;
        while(insertionIndex >= 0 && array[insertionIndex] > cur) {
            array[insertionIndex + 1] = array[insertionIndex];
            insertionIndex--;
        }
        array[insertionIndex + 1] = cur;
    }
}