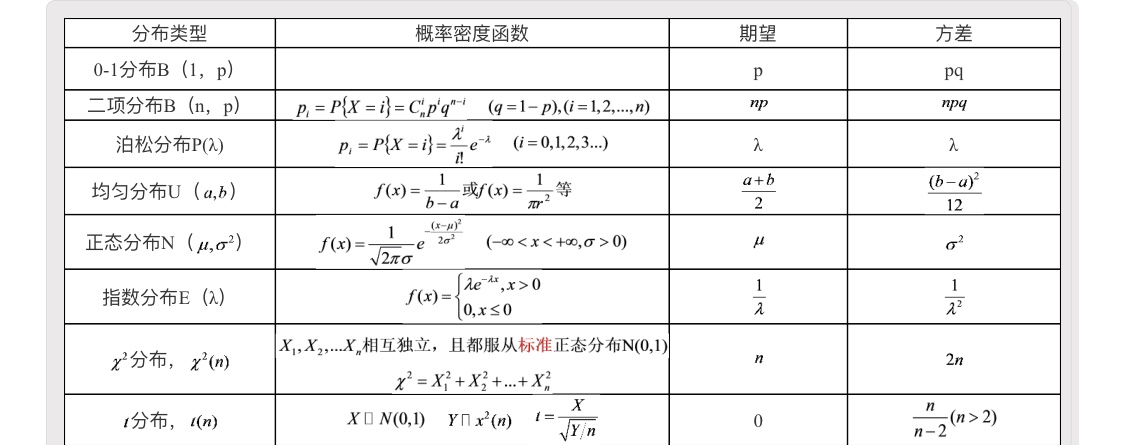
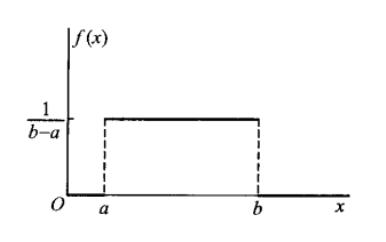
概念

如果对于随机变量X的分布函数F(x)，存在非负可积函数f(x)，使对于任意实数x有
（是一种累积函数）
则称X为连续型随机变量，f(x)称为X的概率密度函数，简称概率密度

性质

1. 
2. 
3. 对任意实数，,
4. (分布函数)(概率密度)

   均匀分布

   若连续型随机变量X具有概率密度为
   
   则称X在区间（a，b）上服从均匀分布。记为X~U(a，b)
   f(x)概率密度函数图像
   

指数分布

若连续型随机变量X的概率密度为

其中，则称X服从参数为的指数分布
性质：无记忆性，对于任意s,t>0,P{X>s+t|X>s}=P{X>t}

正态分布

![L0_P@~G1@%20E]BZXY51YX.png
若连续型随机变量X的概率密度为
，则服从正态分布，简记为

当时称X服从标准正态分布

引理（标准化）** 若**，则