Pre-graphics

Defer

<script src="file.js" type="module" defer></script>

load the module from the file
dont execute until the page is loaded
window.requestsAnimationFrame(func);

this puts an event on the event queue
it will be some time in the future(nexr frame)
it will happen after current function finishes

Time delta

<script type="module">
        /* Slider 2 - measure the time between iterations */
        let lasttime;  // time
        /** @type{HTMLInputElement} */ let slr = (/** @type{HTMLInputElement} */ document.getElementById("slider2"));
        function advanceSLR(timestamp) {
            let newValue;
            if (lasttime === undefined) {
                newValue = 0;
            } else {
                // doing this in steps to explain...
                const delta = (timestamp - lasttime);       // how many milliseconds since last update
                const change = delta / 1000.0 * 100.0;  // want the slider in 1000ms, but the slider is 100 units
                newValue = (Number(slr.value)+change) % 100;   // move the slider forward
            }
            slr.value = newValue.toString();
            window.requestAnimationFrame(advanceSLR);
            lasttime = timestamp;      // remember the last update
        }
        window.requestAnimationFrame(advanceSLR);  
</script>

<script type="module">
    /* Slider 6 - measure the time between iterations */
    /* this is similar to slider 2, except that we store the "current value"
        ourselves, so we are not subject to rounding errors
     */
    let lasttime;  // time
    let value = 0;
    /** @type{HTMLInputElement} */ let slr = (/** @type{HTMLInputElement} */ document.getElementById("slider6"));
    function advanceSLR(timestamp) {
        if (! (lasttime === undefined)) {
            const delta = (timestamp - lasttime) / 10.0;
            value = (value + delta) % 100;
        }
        slr.value = value.toString();
        window.requestAnimationFrame(advanceSLR);
        lasttime = timestamp;      // remember the last update
    }
    window.requestAnimationFrame(advanceSLR);
</script>

Basic graphics

Representing images types

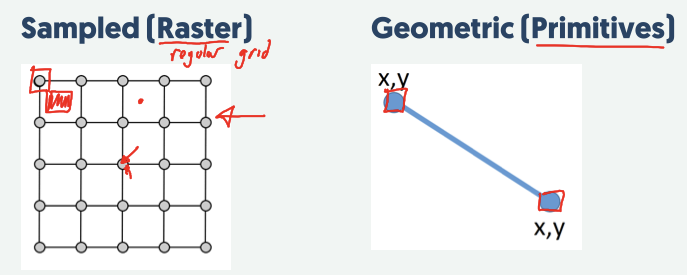
Sampled(raster)
1. LCD/LED/CRT
2. laser printer, inkjet printer
3. film, irregular grid of crystals
Geometric(primitives)
1. pen plotter
2. laser light shows
3. old fashioned vector display
  continuous vs. flicker/strobe
flicker fusion: flashing things seem continues
draw too slowly: double buffering, draw in back
Even / Odd and Winding(Non-zero)

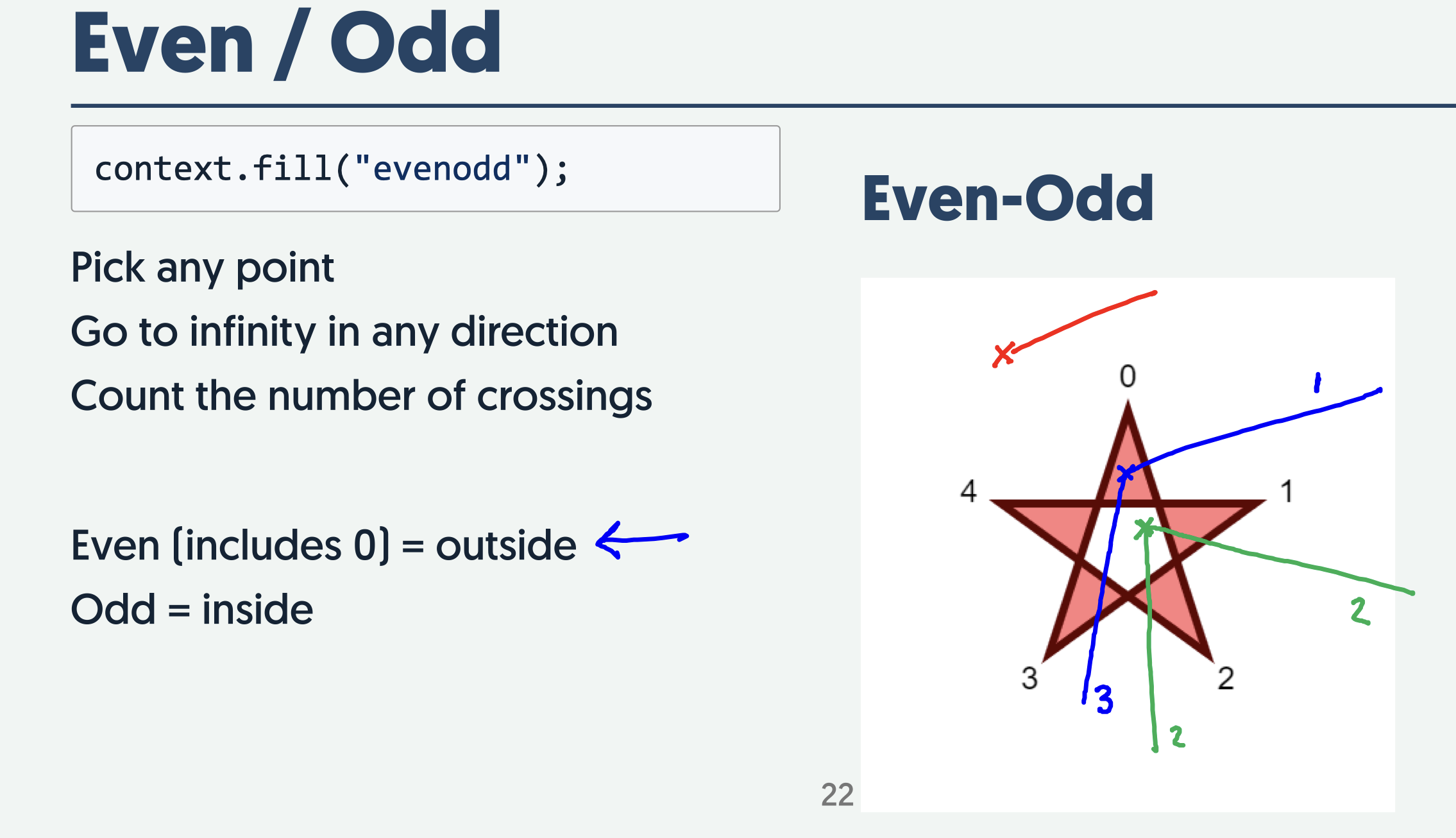
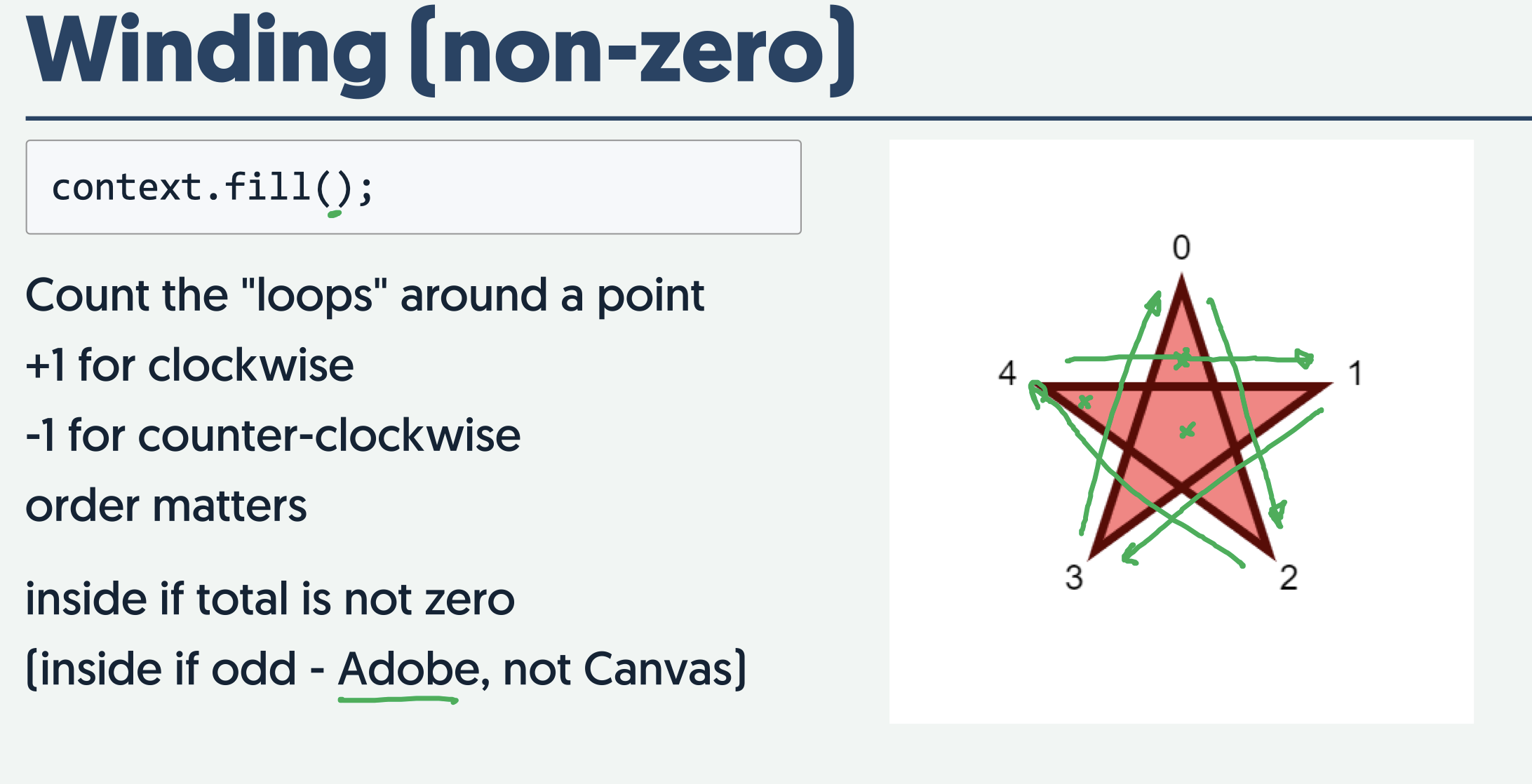
Even/Odd:

Even(includes) -> outside
Odd -> inside

Winding(non-zero):

- 1 for clockwise, -1 for counter-clockwise
total = 0 -> inside,
Web graphics APIs

Canvas 2D
1. an immediate mode 2d drawing library, 1 DOM element for picture
SVG(scalable vector graphics)
1. a display-list(object-based) graphics library
2. grphics objects are DOM elements
WebGL
1. direct access to the graphics hardware
2. require low-level control

Immediate vs. Retained APIs

Canvas is the immediate API, while SVG is the retained API

2D transformation

translate and scale (order matters!)

context.scale(sx, sy); -> scale
context.translate(2,2); -> translate

scale and translate

context.scale(sx,sy);
context.translate(tx,ty);
context.lineTo(X,Y);
means for all X, Y:
context.lineTo(sx(X + tx), sy(Y + ty))

translate and scale

context.translate(tx,ty);
context.scale(sx,sy);
context.lineTo(X,Y);
means for all X, Y:
context.lineTo(tx+(Xsx), ty+(Ysy))

rotation

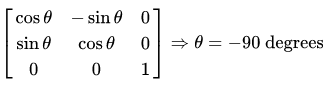
rotate around a point:
context.translate(cx,cy);
context.rotate(angle);
context.translate(-cx, -cy);
drawThing();

skew (shear)

Function composition

x= **h**( **g**( f(**x**))) -> x= (h o g o f)(x)

Homogeneous Coordinates

translate:
[1 0 1 [x [x + 1
0 1 1 y y + 1
0 0 1 ] * 1] = 1]
scale:
[2 0 0
0 2 0
0 0 1]
ATTENTION:
[ 1 0 0
0 1 0
0 0 2 ]
->
[ x/2
y/2
1 ]
2 here means scale by 1/2

Curves

Curves 1

C(n) continuous
C(0) - position, no gaps
C(1) - positions and tangents, no corners, G1 only the direction, but C1 both direction and size
C(2) - positions and tangents and 2nd derivatives (切线大小一样), if C(2), almost must G(2)

Curves 2

Cardinal Cubics - C(1)

Cardinal Splines

The trick to cardinal splines is that we compute the derivatives at any point based on the previous and next point.
s = (1-t) / 2
p′i=s*(pi+1−pi−1), when s = 1/2, we call this cardinal splines

DeCastlejau Constructions

We ues DeCastlejau Constructions to get point position in any position.(when u = what?)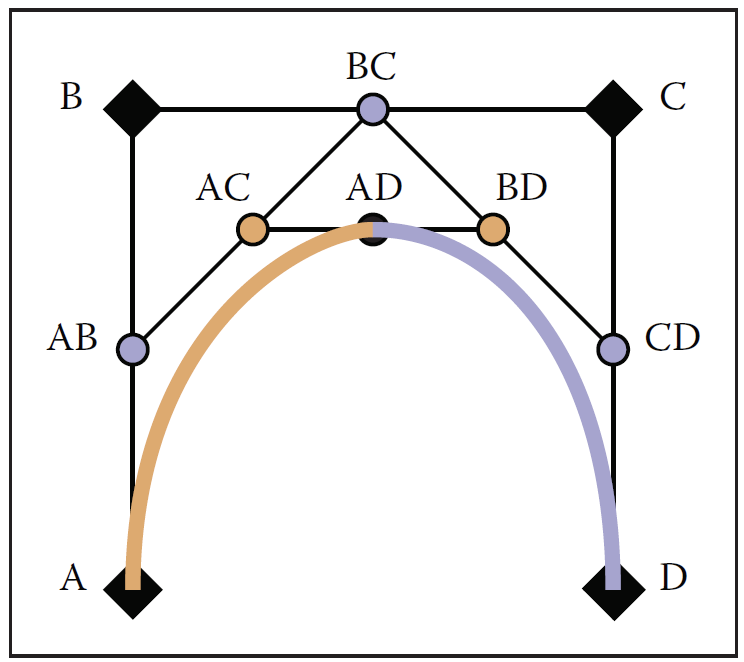

Simple example: [0,8,16,24]
[4,12,20]
[8,16]
[12]
We get the final x value as 12.

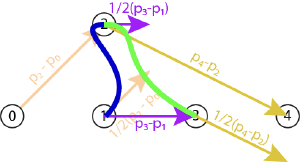
Cubic Bézier Curves

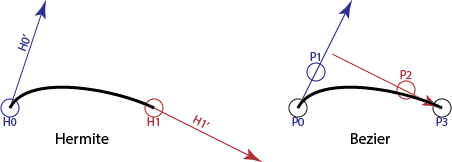
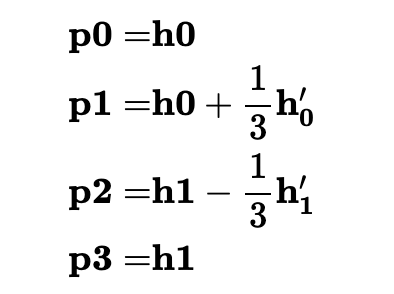
f′(0)=h′0=3(p1−p0)f′(0)=h0′=3(p1−p0)
the tangent is the difference in points times 2 for quadratic

Example:
A curve is made from two Bezier Segments that meet with C(1) continuity.
The first segment is a cubic and has its control points at (0,0), (0,2), (4,6), and (6,6)
The second segment is a quadratic, and has its control points at (6,6), (9,6), (12,0)

the first control point must be the same as the last control point of the previous segment
We know the tangent vector where the curve meets must be 3 ( (6,6)-(4,6) ) or (6,0). So, to have that tangent vector, the quadratic must have its second point at (9,6). (the tangent is the difference in points times 2).

Curves 3

Beziers

Good:

interpolate end-points, stay in convex hull
tangents at ends based on points

Not Good:

not projective invariant
cannot represent conics 圆锥曲线, circle
sometimes we want interpolation

Cardinals (local, next and prev.)
C(1)
local
interpolating

Natural Splines (Cubics) (not local)
C(2)
second derivative is zero at the ends
not local

B-Splines (local) - C(d - 1)
d = 1, line segments [p0,p1], [p1,p2],…[pn-1,pn]
d = 2, quadratics [p0, p1, p2], [p1, p2, p3],..[pn-2, pn-1, pn]
uniform low order polynomial, d = 2 or 3 in graphics
Cubic B-Splines:
1. 4 points influence a curve segment(locally),
2. neighboring segments share 3 points
3. each segment is a cubric polynomial
Locality: each control point influences d+1 segments
Continuity: curve is C(d - 1)
not interpolating

Course Ground🎠

COMP 559 review