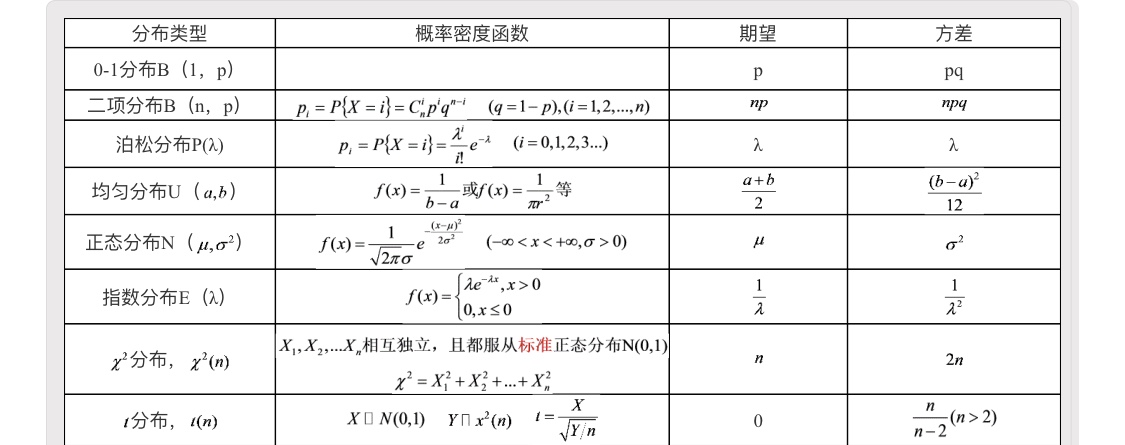
Ch 4.1-2 期望与方差 - 图2

期望

  1. 离散型 Ch 4.1-2 期望与方差 - 图3

  2. 连续型 Ch 4.1-2 期望与方差 - 图4

    期望性质

  3. 设C是常数，则有E(C)=C

  4. 设X是一个随机变量，C是常数 只有 E(CX)=CE(X)
  5. 设X,Y 是两个随机变量，则有 E(X+Y)=E(X)+E(Y)
  6. 设X,Y是相互独立的随机变量，则有 E(XY)=E(X)E(Y)

方差

Ch 4.1-2 期望与方差 - 图5

方差性质

  1. 设X为随机变量，C为常数，则有 Ch 4.1-2 期望与方差 - 图6
  2. 设随机变量X与Y相互独立，则有 Ch 4.1-2 期望与方差 - 图7（重点）

    例题

    | i. 设随机变量X具有(0 - 1)分布，其分布律为
    P{X=0}=1-p, P{X=1}=p. 求D(X)
    解：
    E(X) = 0(1-p)+1p = p
    E(X) = 0(1-p)+1p = p
    D(X) = E(X)-[E(X)] = p-p = p(1-p) | | —- |