归并排序 MergeSort

概念

归并排序也是一种基于归并操作的有效排序算法。在此算法中，我们将一个数组分为两个子数组，通过递归重复将数组切分到只剩下一个元素为止。然后将每个子数组中的元素排序后合并，通过不断合并子数组，最后就会拿到一个排好序的大数组。
归并排序和快排一样，也是一种分而治之算法，简单理解就是将大问题变为小问题，然后把所有小问题都解决掉，大问题就迎刃而解了。其中主要包括两个步骤：

1. 切分步骤：将大问题变为小问题，通过递归解决更小的子问题。
2. 解决步骤：将小问题的结果合并，以此找到大问题的答案。

以数组 [38, 27, 43, 3, 9, 82, 10] 为例，我们通过递归分组，之后原数组被分成长度小于等于2的子数组：

[38, 27], [43, 3], [9, 82], [10]

并将子数组中的元素排序好：

[27, 28], [3, 43], [9, 82], [10]

然后两两合并，归并成排好序的子数组：

[3, 27, 38, 43], [9, 10, 82]

最后将子数组合并为一个排好序的大数组：

[3, 9, 10, 27, 38, 43, 82]

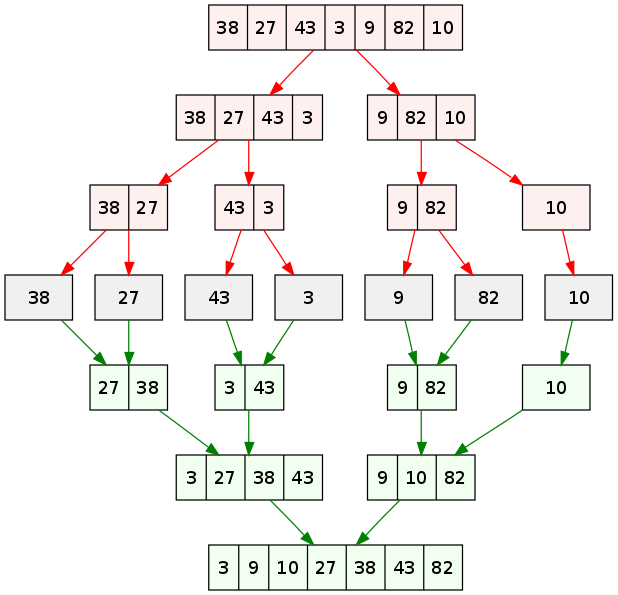
递归具体步骤

1. 递归切分当前数组
2. 如果当前数组数量小于等于1，无需排序，直接返回结果
3. 否则将当前数组分为两个子数组，递归排序这两个子数组
4. 在子数组排序结束后，将子数组的结果归并成排好序的数组

复杂度分析

时间：O(nlogN)
空间：O(N)
在将大问题切分为小问题的过程中，我们每次都将数组切一半，所以需要logN次才能将数组切到一个元素，所以递归的层级就是logN。在每一层中，我们要对子数组进行归并，我们要扫描所有的元素，所以每一层需要N次扫描。那么，时间复杂度就是层级乘以每层的操作 = logN * N = O(NLogN)。在每一层中，我们需要一个临时的数组来存放原先的数据，然后在这个数组中扫描子数组的元素，并将其排好序放回原来的数组，所以空间复杂度就是O(N)。

public void mergeSort(int[] array) {
    int[] helper = copy(array);
    mergeSort(array, helper, 0, array.length - 1);
    return array;
}
public void mergeSort(int[] array, int[] helper, int left, int right) {
    if(right - left < 1) return;
    int mid = left + (right - left) / 2;
    mergeSort(array, helper, left, mid);
    mergeSort(array, helper, mid + 1, right);
    merge(array, helper, left, mid, right);
}
public void merge(int[] array, int[] helper, int left, int mid, int right) {
    for(int i = left; i <= right; i++) {
        helper[i] = array[i];
    }
    int leftStart = left;
    int rightStart = mid + 1;
    for (int i = left; i <= right; i++) { 
        if (leftStart > mid) {   
            array[i] = helper[rightStart++];
        } else if (rightStart > right) {
            array[i] = helper[leftStart++];
        } else if (helper[leftStart] < helper[rightStart]) {
            array[i] = helper[leftStart++];
        } else {
            array[i] = helper[rightStart++];
        }
     }
}
public int[] copy(int[] array) {
     int[] newArray = new int[array.length];
     for(int i = 0; i < array.length; i++) { 
         newArray[i] = array[i];
     }
     return newArray;
}