二分查找 Binary Search

public int BinarySearch(int key, int[] array){
    int left = 0, right = array.length - 1;
    while(left <= right){
        int mid = left + (right - left)/2;
        if(key == array[mid]) return mid;
        if(key < array[mid]) right = mid - 1;
        else left = mid + 1;
    }
    return -1;
}

实现时需要注意以下细节：

1. 在计算 mid 时不能使用 mid = left + right) / 2 这种方式，因为 left + right 可能会导致加法溢出，应该使用 mid = left + (left - right) / 2。
2. 对 h 的赋值和循环条件有关，当循环条件为 left <= right 时，right = mid - 1；当循环条件为 left < right 时，right = mid。解释如下：在循环条件为 left <= right 时，如果 right = mid，会出现循环无法退出的情况，例如 left = 1，right = 1，此时 mid 也等于 1，如果此时继续执行 h = mid，那么就会无限循环；在循环条件为 left < right，如果 right = mid - 1，会错误跳过查找的数，例如对于数组 [1,2,3]，要查找 1，最开始 left = 0，right = 2，mid = 1，判断 key < arr[mid] 执行 right = mid - 1 = 0，此时循环退出，直接把查找的数跳过了。
3. left 的赋值一般都为 left = mid + 1。

Leetcode 69. x的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

方法一： 二分查找

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

class Solution{
    public int mySqrt(int x){
        int left = 0;
        int right = x;
        while(left <= right){
            int mid = left + (right - left) / 2;
            long temp = mid**2;
            if(temp < x){
                left = mid + 1;
            }else if(temp > x){
                right = mid - 1;
            }else if(temp == x){
                return mid;
            }
        }
        //r一定会停在mid**2 <= x的最大那个mid的位置，因为mid**2=x的mid如果存在的话在上面
        //就已经返回了，所以这里只需要返回r就好了
        return right;
    }
}

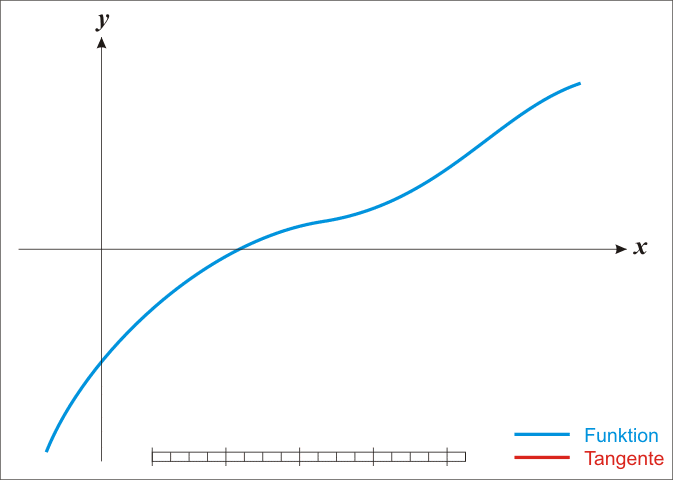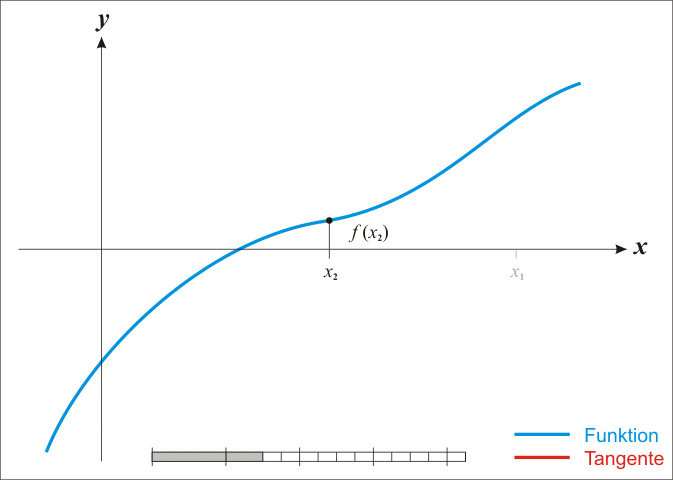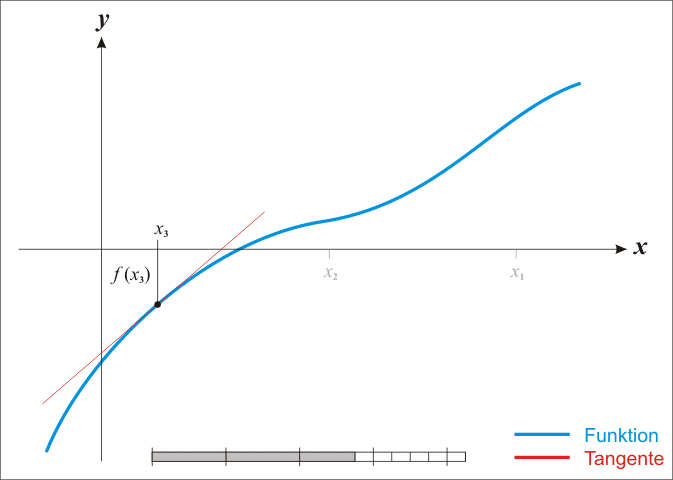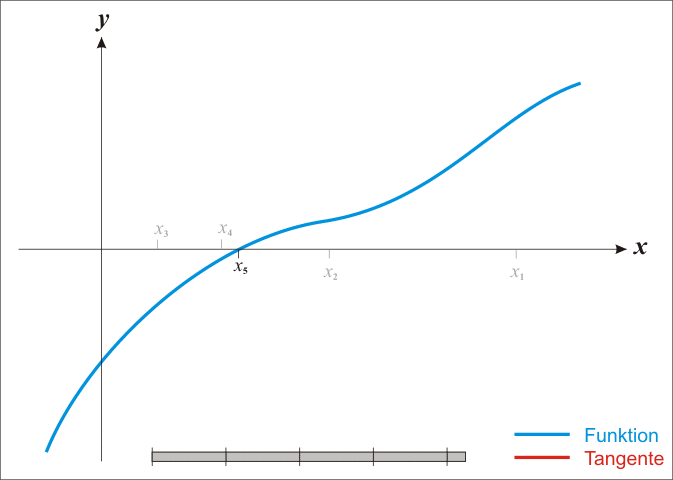
方法二：牛顿法
**

public class Solution {
    public int mySqrt(int a) {
        long x = a;
        while (x * x > a) {
            x = (x + a / x) / 2;
        }
        return (int) x;
    }
}