翻译至https://grisha.org/blog/2016/01/29/triple-exponential-smoothing-forecasting/
这三部分的总结[第二部分第三部分]是我试图对Holt-Winters方法做一个实事求是的解释(和Python代码),对于我们这些人来说,虽然他们假设自己在数学方面可能很在行,但仍然会在每次机会时尽量避免它。我不得不在修改tgres(它有一个Golang实现)时深入研究这个主题。在发现它有点复杂(但又非常简单)之后,我想分享这些知识是很好的,在这个过程中,我也希望能巩固它。
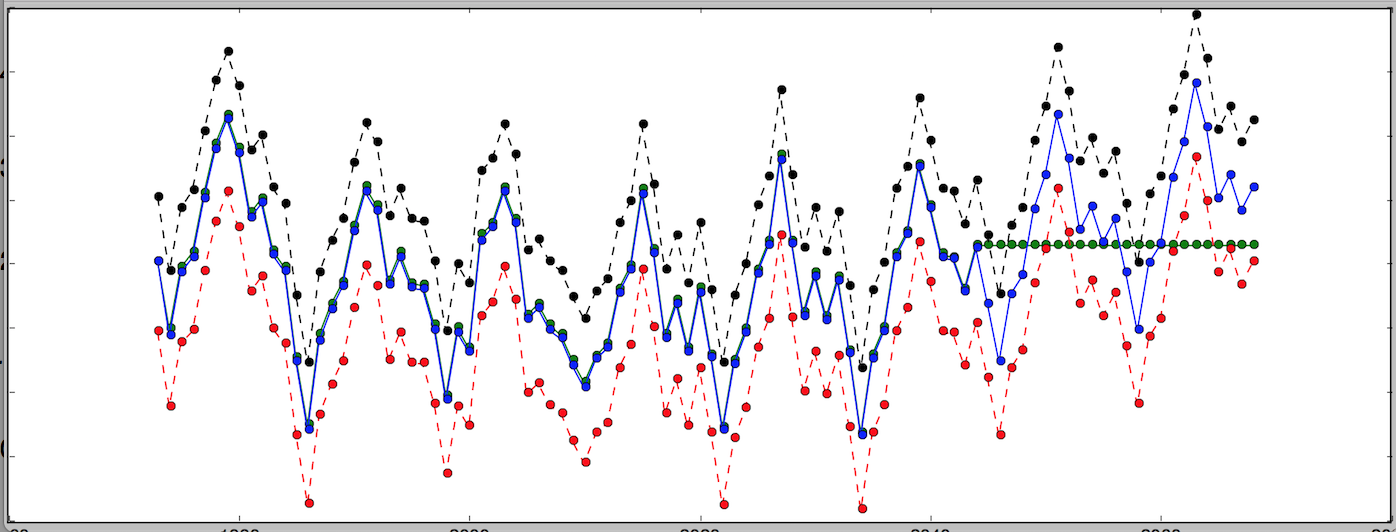
三指数平滑,也称为Holt-Winters方法,是一种可以用来预测序列中数据点的方法或算法,前提是序列是“周期性”的,即在某一时期内重复。
一点历史
**
在某种形式或另一种形式的指数平滑可以追溯到西蒙·泊松(Siméon Poisson,1781-1840)的工作,而它在预测中的应用似乎是一个多世纪后的1956年由罗伯特·布朗(1923-2013)在其出版物《预测需求指数平滑》(Exponential smoothing for Predictive Demand,马萨诸塞州剑桥)中率先提出的。[根据网址,布朗似乎在预测烟草需求?]
1957年,麻省理工学院和芝加哥大学的毕业生查尔斯·霍尔特教授(1921-2010)在芝加哥商品大学(当时称为CIT)工作,预测生产、库存和劳动力的趋势。看来霍尔特和布朗是独立工作的,对彼此的工作一无所知。霍尔特发表了一篇论文“用指数加权移动平均数预测趋势和季节”(卡内基理工学院海军研究办公室第52号备忘录)描述了双指数平滑。三年后,1960年,霍尔特的一名学生(?)Peter R.Winters通过添加季节性改进了算法,并通过指数加权移动平均(Management Science 6324–342)发布了预测销售额,引用了Holt博士1957年的论文作为同一主题的早期工作。这个算法被称为三指数平滑或霍尔特温特斯方法,后者可能是因为它在1960年普伦蒂斯霍尔书“计划生产,库存和劳动力”霍尔特,莫迪利亚尼,穆思,西蒙,博尼尼和温特斯描述-祝你好运找到一个副本!
奇怪的是,我在网上找不到彼得·温特斯的任何个人信息。如果你有什么发现,请告诉我,我会在这里添加一个参考。
2000年,当Jake D.Brutlag(时任WebTV)在《网络监控时间序列》(第14届系统管理会议记录,LISA 2000)上发表《异常行为检测》(Aberrant Behavior Detection)时,Holt-Winters方法在互联网服务提供商圈子里广为人知。它描述了Holt-Winters季节性方法的一个变体的开源C实现(实现链接)如何用于监视网络流量,Holt-Winters季节性方法是他为非常流行的ISPs RRDTool提供的一个特性。
2003年,温特斯论文发表40多年来,牛津大学的James W Taylor教授将Holt-Winters方法推广到多季节性(即n次指数平滑),并发表了使用双季节指数平滑的短期电力需求预测(运筹学学会杂志,第54卷,第799-805页)。(但我们这里不讨论泰勒方法)。
2011年,由Brutlag贡献的RRDTool实现由Matthew Graham移植到Graphite,从而使它在devops社区中更加流行。
那么…它是怎么工作的?
预测,第一小小步
**
解释三指数平滑的最好方法是从最简单的预测方法开始逐步建立。为了避免文本太长,我们将停止使用三次指数平滑,尽管还有很多其他方法已知。
我只在我认为最有意义的地方使用数学符号,有时还附带一个“英语翻译”,并在适当的地方补充一些Python代码。在Python中,我避免使用任何非标准的包,保持示例的简洁。为了清楚起见,我选择不使用发电机。这里的目标是解释算法的内部工作,以便您可以用自己喜欢的任何语言实现它。
我也希望能证明,这足够简单,你不需要求助于SciPy或其他什么(不是说有什么问题)。
但首先,一些术语
系列(series)
这里的主题是一个系列。在现实世界中,我们很可能将其应用于时间序列,但对于这个讨论来说,时间方面是不相关的。序列只是一个有序的数字序列。我们可能使用的词在性质上是按时间顺序排列的(过去,未来,但,已经,甚至时间!),但这只是因为它让人更容易理解。所以忘记时间,时间戳,间隔,时间不存在,每个数据点唯一的属性(除了值)是它的顺序:第一,下一,前一,最后,等等。
把一个序列看作二维x,y坐标的列表是有用的,其中x是顺序(总是向上1),y是值。由于这个原因,在我们的数学公式中,我们将坚持y代表值,x代表顺序。
观察与预期
预测是根据我们所知道的值来估计我们还不知道的值。我们知道的值被称为观察值,而我们预测的值是预期值。表示期望值的数学约定是用扬抑符a.k.a.“hat”:ŷ
例如,如果我们有一个类似于[1,2,3]的序列,我们可能会预测下一个值为4。使用这个术语,给定观测序列[1,2,3],下一个期望值ŷ4是4。
方法(method)
我们可能根据[1,2,3]直觉得出,在这个数列中,每个值都比前一个值大1,在数学符号中,可以用andŷx+1=yx+1来表示。这个方程式,是我们直觉的结果,被称为预测方法。
如果我们的方法是正确的,那么下一个观测值确实是4,但是如果[1,2,3]实际上是斐波纳契序列的一部分,那么在我们期望的4=4的地方,我们将观测到y4=5。注意前一个表达式中的hattedŷ(预期)和后一个表达式中的y(观察)。
错误,SSE和MSE
在我们已经观测到的情况下,计算期望值是完全正常的。比较两者可以计算出误差,这是观察到的误差和预期的误差之间的差异,是衡量方法准确性的一个不可或缺的指标。
由于差分可以是负数或正数,通常的惯例是使用绝对值或平方误差,使数字始终为正数。对于整个序列,平方误差通常求和得到平方误差之和(SSE)。有时您可能会遇到均方误差(MSE),即简单的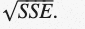
现在的方法(从哪里开始的乐趣!)
在接下来的几个例子中,我们将使用这个小系列:
请随意将它和以下任何代码片段粘贴到Python repl中)
朴素的方法
这是最原始的预测方法。朴素方法的前提是期望点等于最后观测点: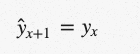
用这种方法我们可以预测下一个点是12。
简单平均数
一种较简单的方法是对所有先前观测到的数据点进行算术平均。我们取所有已知值,计算平均值,并打赌这将是下一个值。当然,这并不是完全正确的,但它可能在球场的某个地方,希望你能看到这种简单化方法背后的原因。
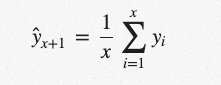
(好的,这个公式在这里只是因为我觉得大写的Sigma看起来很酷。我真诚地希望平均值不需要解释。)在Python中:
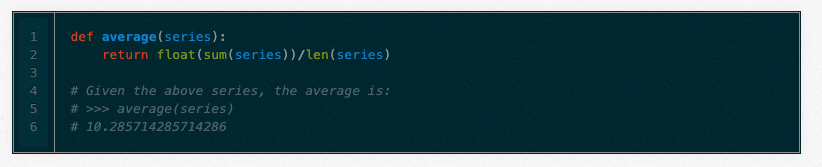
作为一种预测方法,事实上有些情况下它是正确的。例如,你的期末成绩可能是以前所有成绩的平均数。
移动平均值
对简单平均数的改进是n个最后点的平均数。显然,这里的想法是,只有最近的价值观才重要。移动平均数的计算涉及有时被称为大小为n的“滑动窗口”:
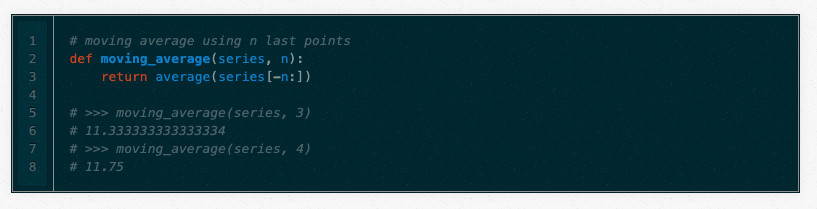
移动平均值实际上是相当有效的,特别是如果你为序列选择了正确的n。股票分析师非常喜欢。
还要注意,简单平均数是移动平均数的一个变体,因此上面的两个函数可以重新编写为一个递归函数:

加权移动平均
加权移动平均是一种移动平均,其中在滑动窗口内的值被赋予不同的权重,通常是为了使最近的点更重要。
它不需要选择窗口大小,而是需要一个权重列表(应该加起来为1)。例如,如果我们选择[0.1,0.2,0.3,0.4]作为权重,我们将分别给最后4个点10%,20%,30%和40%。在Python中:
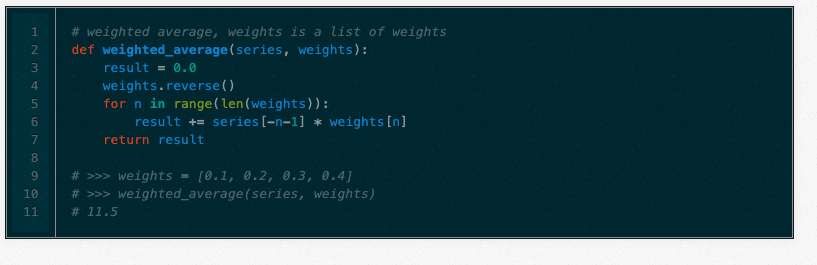
加权移动平均是以下内容的基础,请花点时间来理解它,在阅读之前给它一个思考。
我还要强调重量加起来等于1的重要性。为了说明原因,假设我们选取权重[0.9,0.8,0.7,0.6](加起来是3.0)。注意发生了什么:
拍照时间!
这张图片展示了我们的小系列和所有上述预测。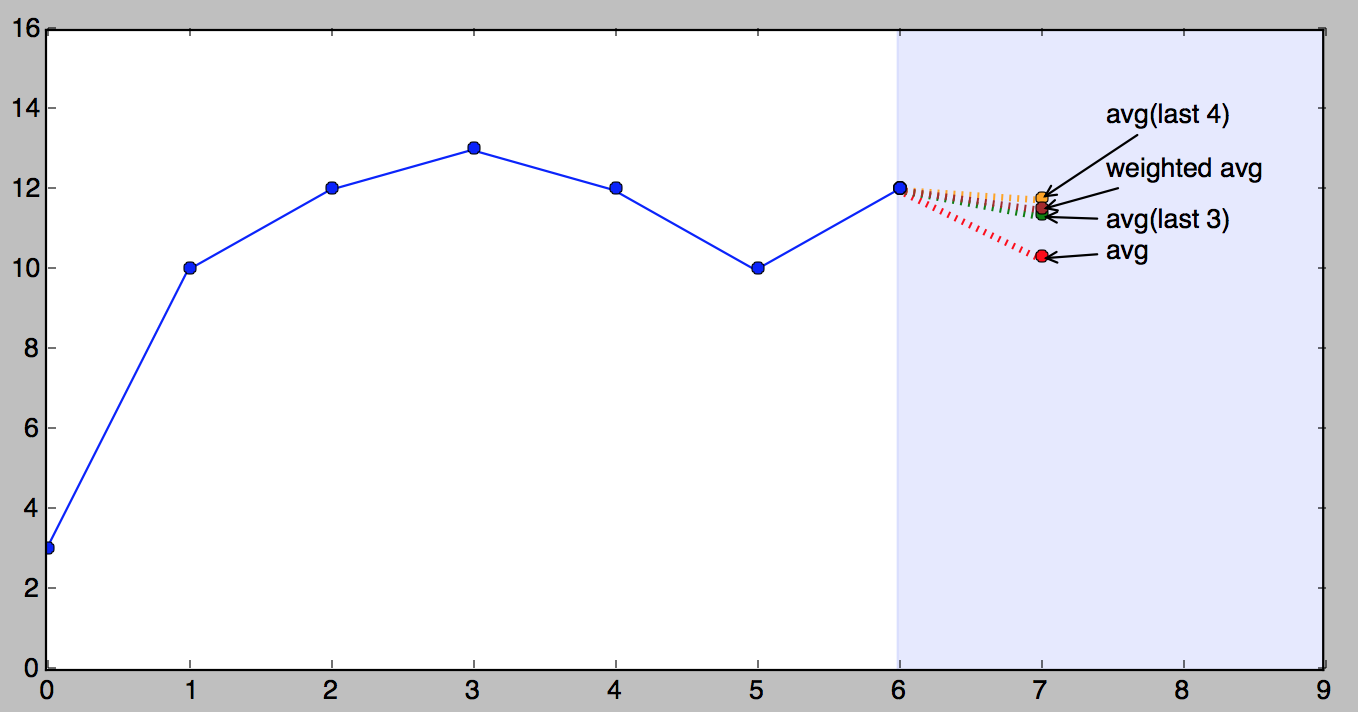
很重要的一点是要知道,以上哪种方法更好在很大程度上取决于级数的性质。我呈现它们的顺序是从简单到复杂,但“更复杂”并不一定意味着“更好”。
单指数平滑
这就是事情变得有趣的地方。想象一下一个加权平均值,我们考虑所有的数据点,当我们回到过去时,按指数分配较小的权重。例如,如果我们从0.9开始,我们的权重将是(回到时间):
…最终接近零点。在某种程度上,这与上面的加权平均非常相似,只是权重由数学决定,均匀衰减。起始重量越小,越快接近零。
只是…有个问题:重量加起来不等于1。前三个数字的总和已经是2.439!(给读者的练习:权重之和接近多少?为什么?)
使泊松、霍尔特或罗伯茨在数学史上占有永久地位的是用一个简洁而优雅的公式来解决这个问题: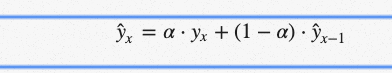
如果你盯着它看足够长的时间,你会看到期望值ŷx是两个产品的总和:α⋅yx和(1–α)⋅xŷ1。在上面(有问题的)例子中,可以将α(alpha)看作是一种起始权重0.9。它被称为平滑因子或平滑系数(取决于谁写了你的课本)。
所以本质上我们得到了一个有两个权重的加权移动平均值:α和1—α。α和1-α之和是1,所以一切都很好。
现在让我们放大求和的右边。聪明的是,1—α乘以先前的期望值ŷx-1。如果你仔细想想,这是同一个公式的结果,它使表达式递归(程序员喜欢递归),如果你把它全部写在纸上,你会很快看到(1—α)一次又一次地乘以它自己,直到数列的开始,如果有一个,否则无穷大。这就是为什么这个方法叫做指数法。
关于α的另一个重要的事情是,它的值决定了我们给出的最近观测值与最后期望值的权重。这是一种杠杆,当它更高(接近1)时,左边的重量更大,当它更低(接近0)时,右边的重量更大。
也许α更好地被称为记忆衰退率:α越高,方法“遗忘”的速度越快。
为什么叫“平滑”?
**
据我所知,这只是指这些方法在绘制值时对图形的影响:锯齿线变得更平滑。移动平均也有同样的效果,所以它也应该被称为平滑。
实施
这种方法的一个方面是程序员会理解的,这一点与数学家无关:它实现起来简单而高效。这是一些蟒蛇。与前面的示例不同,此函数返回整个序列的预期值,而不仅仅是一个点。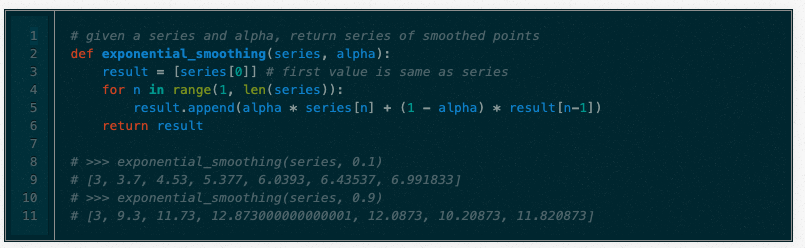
**下图显示了我们系列的指数平滑版本,α为0.9(红色)和α为0.1(橙色)。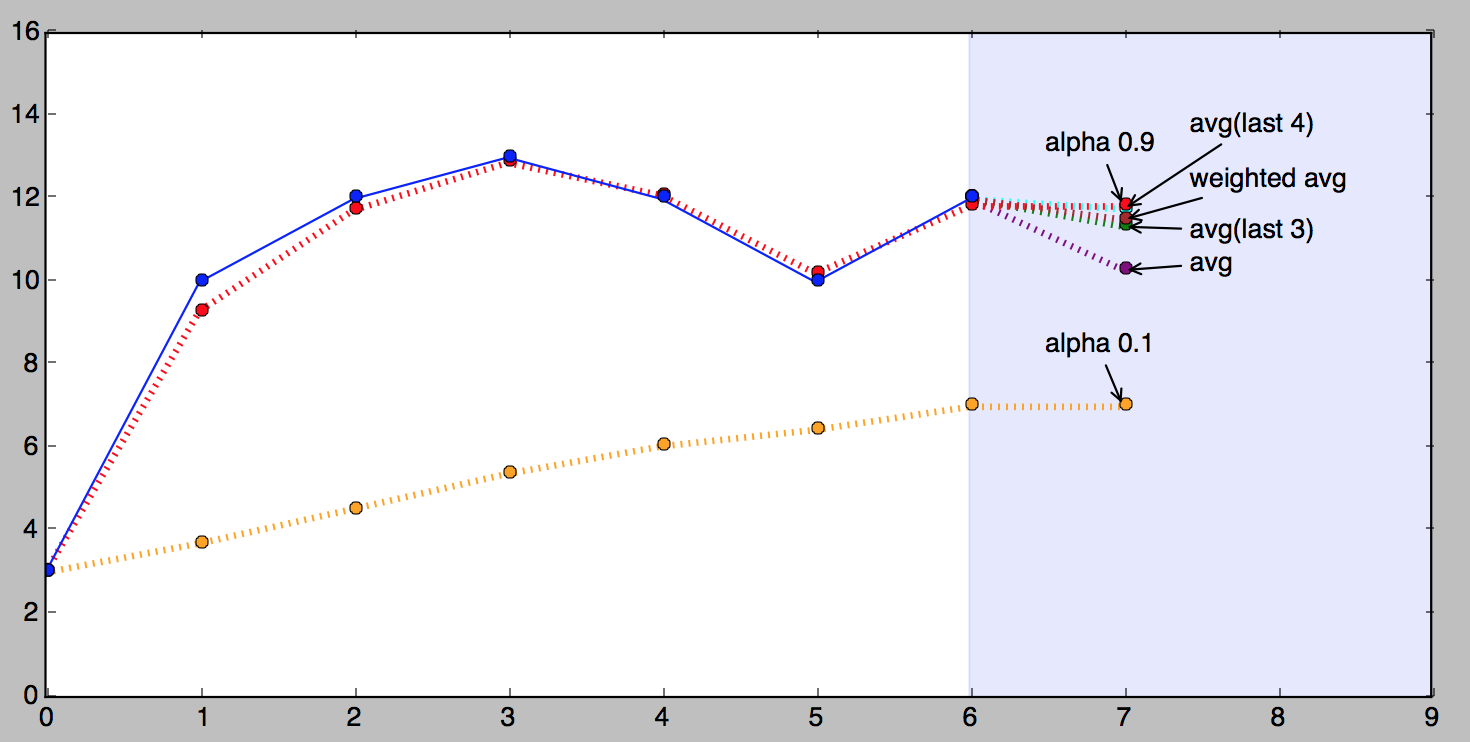
从上图可以看出,0.9的α值与观测值非常接近,远远小于0.1。这对任何序列都不成立,每个序列都有它最好的α(或几个)。找到最佳α的过程称为拟合,我们稍后将单独讨论。
快速回顾
我们已经学习了一些历史,基本术语(系列和它如何不知道时间,方法,错误SSE,MSE和拟合)。我们还学习了一些基本的预测方法:朴素、简单平均、移动平均、加权移动平均,最后是单指数平滑。
上述方法的一个非常重要的特点是,它们只能预测一个点。没错,就一个。
在第二部分中,我们将集中讨论可以预测多个点的方法。

