排序优化

如何选择合适的排序算法？

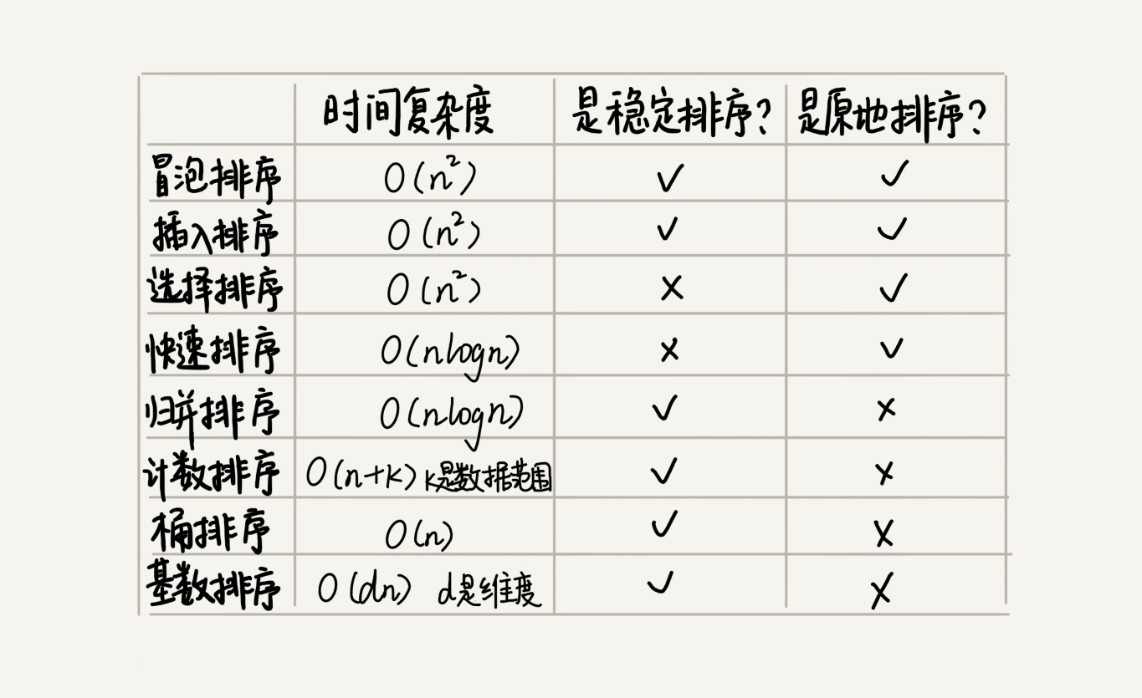
为了兼顾任意规模数据的排序，一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数. 比如 Java 语言采用堆排序实现排序函数，C 语言使用快速排序实现排序函数。

由于归并排序还要O(n)的空间复杂度, 因此实际应用并不多.

如何优化快速排序？

如果数据原来就是有序的或者接近有序的，每次分区点都选择最后一个数据，那快速排序算法就会变得非常糟糕，时间复杂度就会退化为 O(n2)。实际上，这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选得不够合理。

如何来选择分区点呢？
最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

两个常用的分区算法:

1. 三数取中法, 我们从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”。
2. 随机法, 随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。

快速排序是用递归来实现的。我们在递归那一节讲过，递归要警惕堆栈溢出。为了避免快速排序里，递归过深而堆栈过小，导致堆栈溢出，我们有两种解决办法：
第一种是限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归。
第二种是通过在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程，这样就没有了系统栈大小的限制。