递归

递归需要满足的三个条件:
1. 一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
3. 存在递归终止条件

如何编写递归代码？

写递归代码最关键的是写出递推公式，找到终止条件，剩下将递推公式转化为代码就很简单了。

示例:
在电影院, 找出当前是第几排?
用递归解决, 问前一个是第几排, 当前排数=前一排排数+1, 即f(n)=f(n-1)+1,
终止条件为当前一排为第一排时, f(n)=1; 转化为代码如下:

int findRow(int n){
    if(n==1){
        return 1;
    }
    return findRow(n-1);
}

假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？
用递归解决, n个台阶的走法可以分两种大情况:

• 先走1步, 剩下的n-1有f(n-1)种走法
• 先走2步, 剩下的n-2有f(n-2)种走法

翻译成代码为:

f(n)=f(n-1)+f(n-2)

再来看终止条件, 由于f(0)无法计算, 因此终止条件有f(1)=1, f(2)=2, 综上, 代码为:

int findWay(int n){
    if(n==1){
        return 1;
    }
    if(n==2){
        return 2;
    }
    return findWay(n-1)+findWay(n-2);
}

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

如何理解递归?

如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。而且，你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可，不需要一层一层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

因此，编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

递归代码要警惕堆栈溢出

函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

我们可以通过在代码中限制递归调用的最大深度的方式来解决这个问题。递归调用超过一定深度（比如 1000）之后，我们就不继续往下再递归了，直接返回报错。

优化上面第一段代码
// 全局变量，表示递归的深度。
int depth = 0;
int f(int n) {
  ++depth；
  if (depth > 1000) throw exception;
  if (n == 1) return 1;
  return f(n-1) + 1;
}

递归代码要警惕重复计算

例如上面第二个示例, 有大量的重复计算, 可以利用散列表缓存计算结果来优化

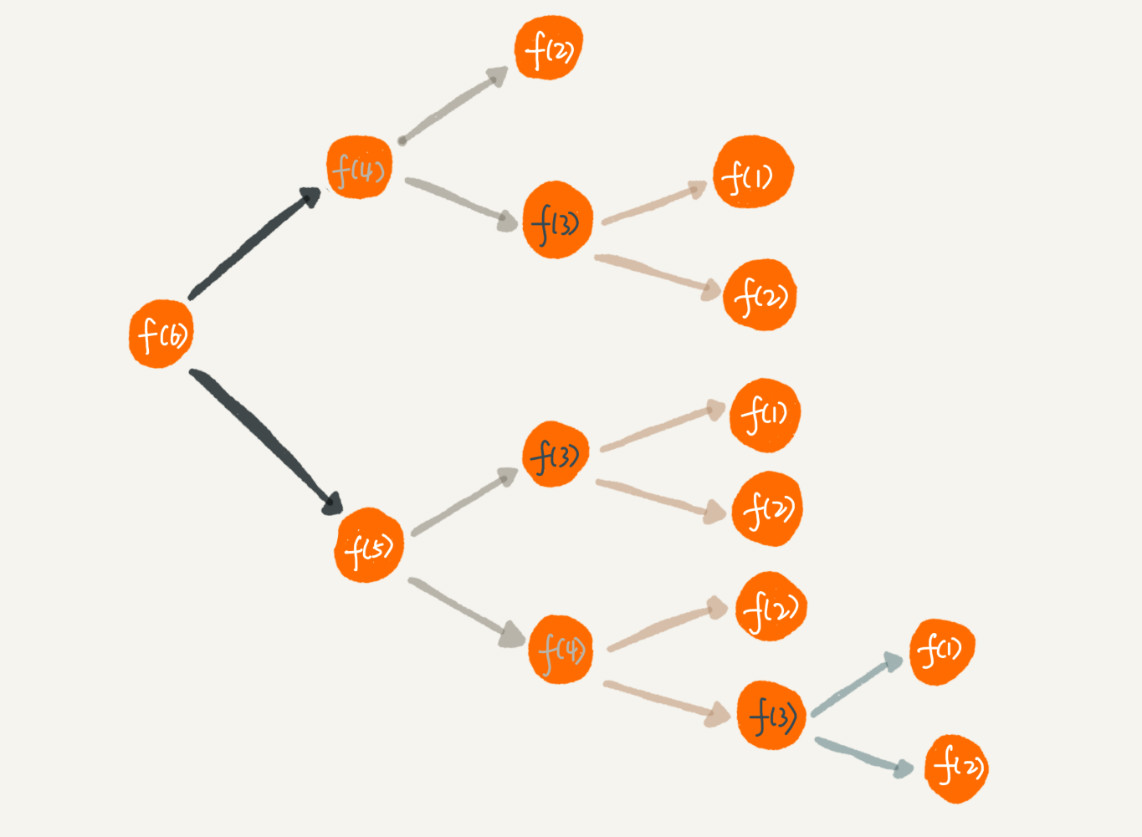
优化第二段示例代码
public int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  // hasSolvedList可以理解成一个Map，key是n，value是f(n)
  if (hasSolvedList.containsKey(n)) {
    return hasSolvedList.get(n);
  }
  int ret = f(n-1) + f(n-2);
  hasSolvedList.put(n, ret);
  return ret;
}

怎么将递归代码改写为非递归代码？

递归有利有弊，利是递归代码的表达力很强，写起来非常简洁；而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题。

笼统的讲，所有的递归代码都可以改写为迭代循环的非递归写法。如何做？抽象出递推公式、初始值和边界条件，然后用迭代循环实现。

优化上面第一段代码
int f(int n) {
  int ret = 1;
  for (int i = 2; i <= n; ++i) {
    ret = ret + 1;
  }
  return ret;
}

优化第二段示例代码
int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  int ret = 0;
  int pre = 2;
  int prepre = 1;
  for (int i = 3; i <= n; ++i) {
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }
  return ret;
}