
还行,就是前面急了,wrong了两次
5976. 检查是否每一行每一列都包含全部整数
对一个大小为 n x n 的矩阵而言,如果其每一行和每一列都包含从 1 到 n 的 全部 整数(含 1 和 n),则认为该矩阵是一个 有效 矩阵。
给你一个大小为 n x n 的整数矩阵 matrix ,请你判断矩阵是否为一个有效矩阵:如果是,返回 true ;否则,返回 false 。
示例 1: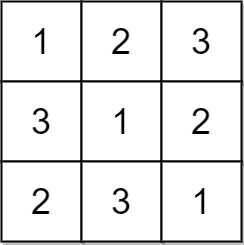
输入:matrix = [[1,2,3],[3,1,2],[2,3,1]] 输出:true 解释:在此例中,n = 3 ,每一行和每一列都包含数字 1、2、3 。 因此,返回 true 。
示例 2: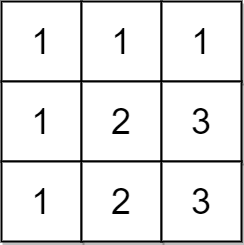
输入:matrix = [[1,1,1],[1,2,3],[1,2,3]] 输出:false 解释:在此例中,n = 3 ,但第一行和第一列不包含数字 2 和 3 。 因此,返回 false 。
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 100
- 1 <= matrix[i][j] <= n
思路:
简单模拟一下
class Solution {public boolean checkValid(int[][] matrix) {int n = matrix.length;boolean[] st = new boolean[n + 1];for (int i = 0; i < n; i++) {Arrays.fill(st, false);for (int j = 0; j < n; j++)st[matrix[i][j]] = true;for (int j = 1; j <= n; j++)if (!st[j]) return false;}for (int j = 0; j < n; j++) {Arrays.fill(st, false);for (int i = 0; i < n; i++)st[matrix[i][j]] = true;for (int i = 1; i <= n; i++)if (!st[i]) return false;}return true;}}
5977. 最少交换次数来组合所有的 1 II
交换 定义为选中一个数组中的两个 互不相同 的位置并交换二者的值。
环形 数组是一个数组,可以认为 第一个 元素和 最后一个 元素 相邻 。
给你一个 二进制环形 数组 nums ,返回在 任意位置 将数组中的所有 1 聚集在一起需要的最少交换次数。
示例 1:
输入:nums = [0,1,0,1,1,0,0] 输出:1 解释:这里列出一些能够将所有 1 聚集在一起的方案: [0,0,1,1,1,0,0] 交换 1 次。 [0,1,1,1,0,0,0] 交换 1 次。 [1,1,0,0,0,0,1] 交换 2 次(利用数组的环形特性)。 无法在交换 0 次的情况下将数组中的所有 1 聚集在一起。 因此,需要的最少交换次数为 1 。
示例 2:
输入:nums = [0,1,1,1,0,0,1,1,0] 输出:2 解释:这里列出一些能够将所有 1 聚集在一起的方案: [1,1,1,0,0,0,0,1,1] 交换 2 次(利用数组的环形特性)。 [1,1,1,1,1,0,0,0,0] 交换 2 次。 无法在交换 0 次或 1 次的情况下将数组中的所有 1 聚集在一起。 因此,需要的最少交换次数为 2 。
示例 3:
输入:nums = [1,1,0,0,1] 输出:0 解释:得益于数组的环形特性,所有的 1 已经聚集在一起。 因此,需要的最少交换次数为 0 。
提示:
- 1 <= nums.length <= 105
- nums[i] 为 0 或者 1
思路:破环成链 + 前缀和
统计1的总数作为滑窗大小,找到最大的滑窗
注意:如果1的个数为0,小心越界!
class Solution {public int minSwaps(int[] nums) {int cnt = 0, n = nums.length;for (int i = 0; i < n; i++)if (nums[i] == 1) cnt++;if (cnt == 0) return 0;int[] a = new int[2 * n];for (int i = 0; i < n; i++)a[i] = a[i + n] = nums[i];int max = 0;for (int i = 1; i < 2 * n; i++)a[i] += a[i - 1];max = a[cnt - 1];for (int i = cnt; i < 2 * n; i++)max = Math.max(max, a[i] - a[i - cnt]);return cnt - max;}}
5978. 统计追加字母可以获得的单词数
给你两个下标从 0 开始的字符串数组 startWords 和 targetWords 。每个字符串都仅由 小写英文字母 组成。
对于 targetWords 中的每个字符串,检查是否能够从 startWords 中选出一个字符串,执行一次 转换操作 ,得到的结果与当前 targetWords 字符串相等。
转换操作 如下面两步所述:
- 追加 任何 不存在 于当前字符串的任一小写字母到当前字符串的末尾。
- 例如,如果字符串为 “abc” ,那么字母 ‘d’、’e’ 或 ‘y’ 都可以加到该字符串末尾,但 ‘a’ 就不行。如果追加的是 ‘d’ ,那么结果字符串为 “abcd” 。
- 重排 新字符串中的字母,可以按 任意 顺序重新排布字母。
- 例如,”abcd” 可以重排为 “acbd”、”bacd”、”cbda”,以此类推。注意,它也可以重排为 “abcd” 自身。
找出 targetWords 中有多少字符串能够由 startWords 中的 任一 字符串执行上述转换操作获得。返回 _targetWords _中这类 字符串的数目 。
注意:你仅能验证 targetWords 中的字符串是否可以由 startWords 中的某个字符串经执行操作获得。startWords 中的字符串在这一过程中 不 发生实际变更。
示例 1:
输入:startWords = [“ant”,”act”,”tack”], targetWords = [“tack”,”act”,”acti”] 输出:2 解释: - 为了形成 targetWords[0] = “tack” ,可以选用 startWords[1] = “act” ,追加字母 ‘k’ ,并重排 “actk” 为 “tack” 。 - startWords 中不存在可以用于获得 targetWords[1] = “act” 的字符串。 注意 “act” 确实存在于 startWords ,但是 必须 在重排前给这个字符串追加一个字母。 - 为了形成 targetWords[2] = “acti” ,可以选用 startWords[1] = “act” ,追加字母 ‘i’ ,并重排 “acti” 为 “acti” 自身。
示例 2:
输入:startWords = [“ab”,”a”], targetWords = [“abc”,”abcd”] 输出:1 解释: - 为了形成 targetWords[0] = “abc” ,可以选用 startWords[0] = “ab” ,追加字母 ‘c’ ,并重排为 “abc” 。 - startWords 中不存在可以用于获得 targetWords[1] = “abcd” 的字符串。
提示:
- 1 <= startWords.length, targetWords.length <= 5 * 104
- 1 <= startWords[i].length, targetWords[j].length <= 26
- startWords 和 targetWords 中的每个字符串都仅由小写英文字母组成
- 在 startWords 或 targetWords 的任一字符串中,每个字母至多出现一次
思路:
注意题意是两个转换操作都得执行
用字典树存储startWords数组中的每一个字符串转换后的所有串,按从小到大的字母顺序
查询targetWords中的串排序后是否在字典树中出现即可
class Solution {public int wordCount(String[] s, String[] t) {int n = t.length;Trie trie = new Trie();for (String ss : s) {trie.insert(ss);}int cnt = 0;for (String ss : t) {if (trie.query(ss))cnt++;}return cnt;}}class Trie {class TrieNode {TrieNode[] son = new TrieNode[26];boolean end;}TrieNode root = new TrieNode();void insert(String s) {char[] ch = s.toCharArray();boolean[] st = new boolean[26];for (char c : ch)st[c - 'a'] = true;char[] cc = new char[ch.length + 1];int len = ch.length;for (int i = 0; i < 26; i++) {if (!st[i]) {System.arraycopy(ch, 0, cc, 0, ch.length);cc[len] = (char)(i + 'a');Arrays.sort(cc);insert(cc);}}}void insert(char[] ch) {TrieNode cur = root;for (int i = 0; i < ch.length; i++) {int idx = ch[i] - 'a';if (cur.son[idx] == null)cur.son[idx] = new TrieNode();cur = cur.son[idx];}cur.end = true;}boolean query(String s) {char[] ch = s.toCharArray();Arrays.sort(ch);TrieNode cur = root;for (int i = 0; i < ch.length; i++) {int idx = ch[i] - 'a';if (cur.son[idx] == null) {return false;}cur = cur.son[idx];}return cur.end;}}
5979. 全部开花的最早一天


你有 n 枚花的种子。每枚种子必须先种下,才能开始生长、开花。播种需要时间,种子的生长也是如此。给你两个下标从 0 开始的整数数组 plantTime 和 growTime ,每个数组的长度都是 n :
- plantTime[i] 是 播种 第 i 枚种子所需的 完整天数 。每天,你只能为播种某一枚种子而劳作。无须 连续几天都在种同一枚种子,但是种子播种必须在你工作的天数达到 plantTime[i] 之后才算完成。
- growTime[i] 是第 i 枚种子完全种下后生长所需的 完整天数 。在它生长的最后一天 之后 ,将会开花并且永远 绽放 。
从第 0 开始,你可以按 任意 顺序播种种子。
返回所有种子都开花的 最早 一天是第几天。
示例 1:
输入:plantTime = [1,4,3], growTime = [2,3,1] 输出:9 解释:灰色的花盆表示播种的日子,彩色的花盆表示生长的日子,花朵表示开花的日子。 一种最优方案是: 第 0 天,播种第 0 枚种子,种子生长 2 整天。并在第 3 天开花。 第 1、2、3、4 天,播种第 1 枚种子。种子生长 3 整天,并在第 8 天开花。 第 5、6、7 天,播种第 2 枚种子。种子生长 1 整天,并在第 9 天开花。 因此,在第 9 天,所有种子都开花。
示例 2:
输入:plantTime = [1,2,3,2], growTime = [2,1,2,1] 输出:9 解释:灰色的花盆表示播种的日子,彩色的花盆表示生长的日子,花朵表示开花的日子。 一种最优方案是: 第 1 天,播种第 0 枚种子,种子生长 2 整天。并在第 4 天开花。 第 0、3 天,播种第 1 枚种子。种子生长 1 整天,并在第 5 天开花。 第 2、4、5 天,播种第 2 枚种子。种子生长 2 整天,并在第 8 天开花。 第 6、7 天,播种第 3 枚种子。种子生长 1 整天,并在第 9 天开花。 因此,在第 9 天,所有种子都开花。
示例 3:
输入:plantTime = [1], growTime = [1] 输出:2 解释:第 0 天,播种第 0 枚种子。种子需要生长 1 整天,然后在第 2 天开花。 因此,在第 2 天,所有种子都开花。
提示:
- n == plantTime.length == growTime.length
- 1 <= n <= 105
- 1 <= plantTime[i], growTime[i] <= 104
思路:
贪心题
种树时间是必须全部累加,所以只需要按成长时间从大到小排就行了,然后扫描一遍,找到最大开花时间
class Solution {public int earliestFullBloom(int[] p, int[] g) {int n = p.length;int[][] a = new int[n][2];for (int i = 0; i < n; i++) {a[i][0] = p[i];a[i][1] = g[i];}Arrays.sort(a, (o1, o2) -> (o2[1] - o1[1]));int max = 0;int cnt = 0;for (int i = 0; i < n; i++) {max = Math.max(a[i][0] + a[i][1] + cnt, max);cnt += a[i][0];}return max;}}

