image.png
无Wrong，t4又是DP。

6104. 统计星号

给你一个字符串 s ，每 两个 连续竖线 ‘|’ 为 一对 。换言之，第一个和第二个 ‘|’ 为一对，第三个和第四个 ‘|’ 为一对，以此类推。
请你返回 不在 竖线对之间，s 中 ‘‘ 的数目。
注意，每个竖线 ‘|’ 都会 *恰好 属于一个对。

示例 1：
输入：s = “l|eet|co|*de|” 输出：2 解释：不在竖线对之间的字符加粗加斜体后，得到字符串：”l|eet|c**o|*de|” 。 第一和第二条竖线 ‘|’ 之间的字符不计入答案。 同时，第三条和第四条竖线 ‘|’ 之间的字符也不计入答案。 不在竖线对之间总共有 2 个星号，所以我们返回 2 。
示例 2：
输入：s = “iamprogrammer” 输出：0 解释：在这个例子中，s 中没有星号。所以返回 0 。
示例 3：
输入：s = “yo|uar|e|b|e*au|tifu|l” 输出：5 解释：需要考虑的字符加粗加斜体后：”yo|uar|e**|b|e*au|tifu|l**” 。不在竖线对之间总共有 5 个星号。所以我们返回 5 。

提示：

  • 1 <= s.length <= 1000
  • s 只包含小写英文字母，竖线 ‘|’ 和星号 ‘*’ 。
  • s 包含 偶数 个竖线 ‘|’ 。

思路：
遍历搜即可

  1. class Solution {
  2.     public int countAsterisks(String s) {
  3.         int cnt = 0;
  4.         boolean flag = false;
  5.         for (int i = 0; i < s.length(); i++) {
  6.             if (s.charAt(i) == '|') {
  7.                 flag = flag ? false : true;
  8.             } else if (s.charAt(i) == '*') {
  9.                 if (!flag) cnt++;
  10.             }
  11.         }
  12.         return cnt;
  13.     }
  14. }

6106. 统计无向图中无法互相到达点对数

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。

示例 1：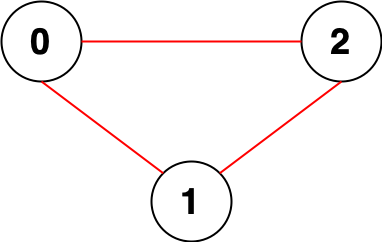
image.png
输入：n = 3, edges = [[0,1],[0,2],[1,2]] 输出：0 解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。
示例 2：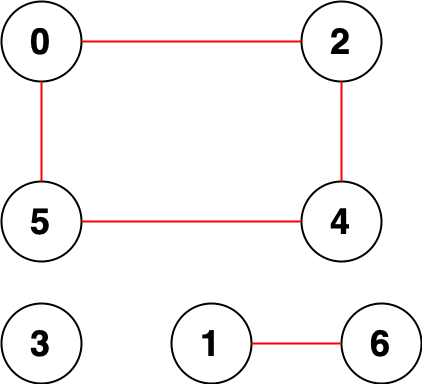
image.png
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]] 输出：14 解释：总共有 14 个点对互相无法到达： [[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]] 所以我们返回 14 。

提示：

  • 1 <= n <= 105
  • 0 <= edges.length <= 2 * 105
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • 不会有重复边。

思路：
并查集维护连通块内的元素数

  1. class Solution {
  2.     int N = 100010;
  3.     int[] fa = new int[N];
  4.     int[] cnt = new int[N];
  5.     int find(int x) {
  6.         return fa[x] == x ? x : (fa[x] = find(fa[x]));
  7.     }
  9.     void merge(int x, int y) {
  10.         int px = find(x), py = find(y);
  11.         if (px != py) {
  12.             fa[px] = py;
  13.             cnt[py] += cnt[px];
  14.         }
  15.     }
  17.     public long countPairs(int n, int[][] edges) {
  18.         long res = 0;
  20.         for (int i = 0; i < n; i++) {
  21.             fa[i] = i;
  22.             cnt[i] = 1;
  23.         }
  25.         for (int[] e : edges) {
  26.             int a = e[0], b = e[1];
  27.             merge(a, b);
  28.         }
  30.         for (int i = 0; i < n; i++) {
  31.             int other = n - cnt[find(i)];
  32.             res += other;
  33.         }
  34.         return res / 2;
  35.     }
  36. }

6105. 操作后的最大异或和

给你一个下标从 0 开始的整数数组 nums 。一次操作中，选择 任意 非负整数 x 和一个下标 i ，更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。
注意，AND 是逐位与运算，XOR 是逐位异或运算。
请你执行 任意次 更新操作，并返回 nums 中所有元素 最大 逐位异或和。

示例 1：
输入：nums = [3,2,4,6] 输出：7 解释：选择 x = 4 和 i = 3 进行操作，num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。 现在，nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。 可知 7 是能得到的最大逐位异或和。 注意，其他操作可能也能得到逐位异或和 7 。
示例 2：
输入：nums = [1,2,3,9,2] 输出：11 解释：执行 0 次操作。 所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。 可知 11 是能得到的最大逐位异或和。

提示：

  • 1 <= nums.length <= 105
  • 0 <= nums[i] <= 108

思路：
贪心，统计所有数字的或

  1. class Solution {
  2.     public int maximumXOR(int[] nums) {
  3.         int res = 0;
  4.         for (int x : nums) {
  5.             res |= x;
  6.         }
  7.         return res;
  8.     }
  9. }

6107. 不同骰子序列的数目

给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下，求出 不同 骰子序列的数目：

  1. 序列中任意 相邻 数字的 最大公约数 为 1 。
  2. 序列中 相等 的值之间，至少有 2 个其他值的数字。正式地，如果第 i 次掷骰子的值 等于 第 j 次的值，那么 abs(i - j) > 2 。

请你返回不同序列的 总数目 。由于答案可能很大，请你将答案对 109 + 7 取余 后返回。
如果两个序列中至少有一个元素不同，那么它们被视为不同的序列。

示例 1：
输入：n = 4 输出：184 解释：一些可行的序列为 (1, 2, 3, 4) ，(6, 1, 2, 3) ，(1, 2, 3, 1) 等等。 一些不可行的序列为 (1, 2, 1, 3) ，(1, 2, 3, 6) 。 (1, 2, 1, 3) 是不可行的，因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 （下标从 1 开始表示）。 (1, 2, 3, 6) i是不可行的，因为 3 和 6 的最大公约数是 3 。 总共有 184 个不同的可行序列，所以我们返回 184 。
示例 2：
输入：n = 2 输出：22 解释：一些可行的序列为 (1, 2) ，(2, 1) ，(3, 2) 。 一些不可行的序列为 (3, 6) ，(2, 4) ，因为最大公约数不为 1 。 总共有 22 个不同的可行序列，所以我们返回 22 。

提示：

  • 1 <= n <= 104

思路：
DP
状态表示：f[i][j][k]表示前i个元素，且最后一位是j倒数第二位为k的所有可行方案
属性：总数目

  1. class Solution {
  2.     public int distinctSequences(int n) {
  3.         if (n == 1) return 6;
  4.         if (n == 2) return 22;
  5.         int MOD = (int)(1e9 + 7);
  6.         boolean[][] used = new boolean[7][7];
  7.         for (int i = 1; i <= 6; i++) {
  8.             for (int j = 1; j <= 6; j++) {
  9.                 if (j == i) continue;
  10.                 if (gcd(i, j) == 1)
  11.                     used[i][j] = true;
  12.             }
  13.         }
  16.         int[][][] f = new int[n + 1][7][7];
  18.         for (int i = 1; i <= 6; i++)
  19.             for (int j = 1; j <= 6; j++) {
  20.                 if (used[i][j])
  21.                     f[2][i][j] = 1;
  22.             }
  24.         for (int i = 3; i <= n; i++) {
  25.             for (int j = 1; j <= 6; j++) {
  26.                 for (int k = 1; k <= 6; k++) {
  27.                     if (!used[j][k]) continue;
  28.                     for (int x = 1; x <= 6; x++) {
  29.                         if (!used[k][x] || j == x) continue;
  30.                         f[i][j][k] = (f[i][j][k] + f[i - 1][k][x]) % MOD;
  31.                     }
  32.                 }
  33.             }
  34.         }
  36.         int res = 0;
  37.         for (int i = 1; i <= 6; i++) {
  38.             for (int j = 1; j <= 6; j++) {
  39.                 if (used[i][j]) {
  40.                     res = (res + f[n][i][j]) % MOD;
  41.                 }
  42.             }
  43.         }
  44.         return res;
  45.     }
  47.     int gcd(int a, int b) {
  48.         return b == 0 ? a : gcd(b, a % b);
  49.     }
  50. }