周赛 - 🏆 第 299 场力扣周赛 - 《学习笔记》

6101. 判断矩阵是否是一个 X 矩阵
6100. 统计放置房子的方式数
5229. 拼接数组的最大分数
6103. 从树中删除边的最小分数

第一题没看懂题，差点放弃，还好坚持了一下，t2和t3都是DP，最近的DP真多啊。

6101. 判断矩阵是否是一个 X 矩阵

如果一个正方形矩阵满足下述全部条件，则称之为一个 X 矩阵 ：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 _grid _是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：
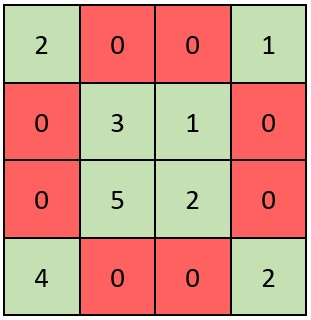
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]] 输出：true 解释：矩阵如上图所示。 X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。因此，grid 是一个 X 矩阵。
示例 2：
输入：grid = [[5,7,0],[0,3,1],[0,5,0]] 输出：false 解释：矩阵如上图所示。 X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。因此，grid 不是一个 X 矩阵。

提示：

n == grid.length == grid[i].length
3 <= n <= 100
0 <= grid[i][j] <= 105

思路：
判断每一个数即可

class Solution {
    public boolean checkXMatrix(int[][] g) {
        int n = g.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i == j || i + j == n - 1) {
                    if (g[i][j] == 0) return false;
                } else {
                    if (g[i][j] != 0) return false;
                }
            }
        }
        return true;
    }
}

6100. 统计放置房子的方式数

一条街道上共有 n 2 个 *地块 ，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。
现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 109 + 7 取余后再返回。
注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例 1：
输入：n = 1 输出：4 解释： 可能的放置方式： 1. 所有地块都不放置房子。 2. 一所房子放在街道的某一侧。 3. 一所房子放在街道的另一侧。 4. 放置两所房子，街道两侧各放置一所。
示例 2：
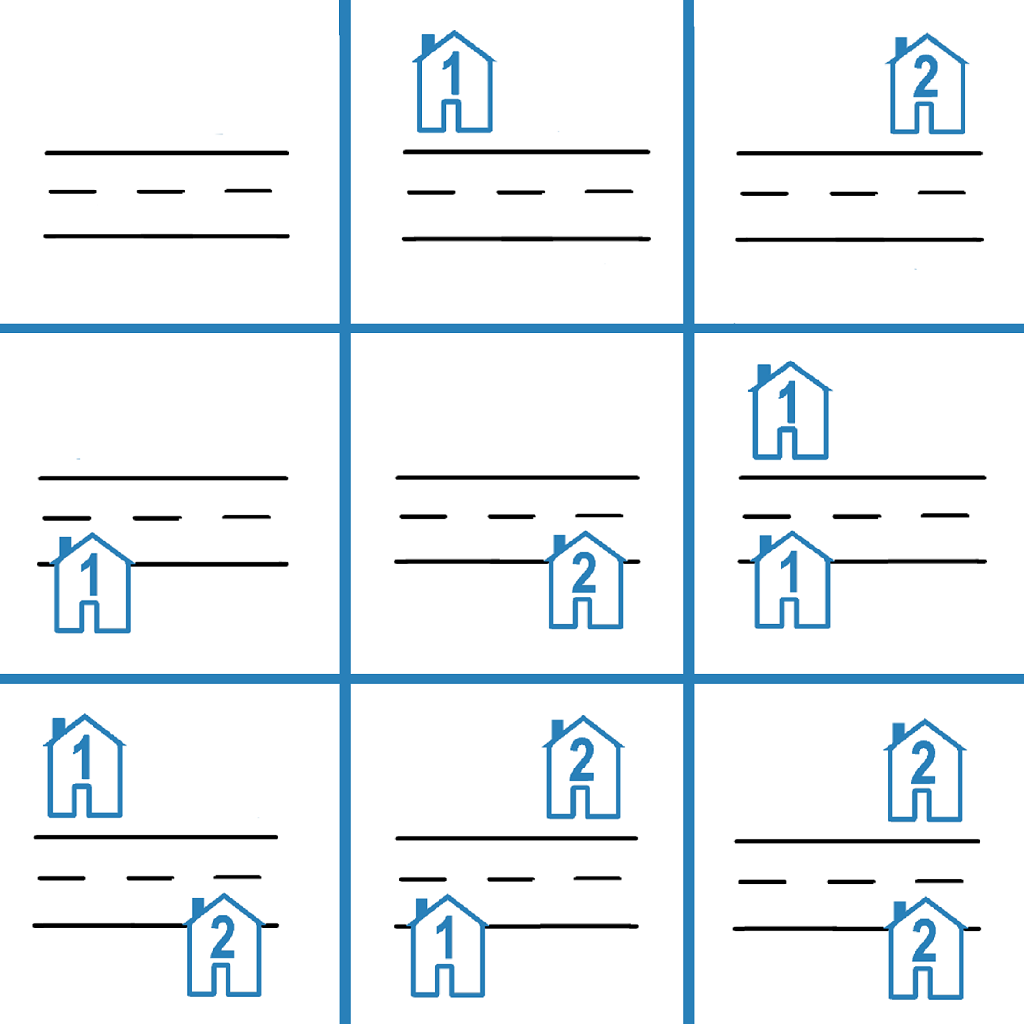
输入：n = 2 输出：9 解释：如上图所示，共有 9 种可能的放置方式。

提示：

1 <= n <= 104

思路：
状态机DP

class Solution {
    public int countHousePlacements(int n) {
        int MOD = (int)(1e9 + 7);
        int[][] f = new int[n + 1][4];
        for (int i = 0; i < 4; i++)
            f[1][i] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < 4; j++) {
                for (int k = 0; k < 4; k++) {
                    if ((j & k) == 0) {
                        f[i][j] = (f[i][j] + f[i - 1][k]) % MOD;
                    }
                }
            }
        }
        int sum = 0;
        for (int i = 0; i < 4; i++)
            sum = (sum + f[n][i]) % MOD;
        return sum;
    }
}

5229. 拼接数组的最大分数

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度都是 n 。
你可以选择两个整数 left 和 right ，其中 0 <= left <= right < n ，接着交换两个子数组 nums1[left…right] 和 nums2[left…right] 。

例如，设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ，整数选择 left = 1 和 right = 2，那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。

你可以选择执行上述操作一次或不执行任何操作。
数组的分数取 sum(nums1) 和 sum(nums2) 中的最大值，其中 sum(arr) 是数组 arr 中所有元素之和。
返回 可能的最大分数 。
子数组 是数组中连续的一个元素序列。arr[left…right] 表示子数组包含 nums 中下标 left 和 right 之间的元素（含下标 left 和 right 对应元素）。

示例 1：
输入：nums1 = [60,60,60], nums2 = [10,90,10] 输出：210 解释：选择 left = 1 和 right = 1 ，得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。
示例 2：
输入：nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20] 输出：220 解释：选择 left = 3 和 right = 4 ，得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。
示例 3：
输入：nums1 = [7,11,13], nums2 = [1,1,1] 输出：31 解释：选择不交换任何子数组。分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。

提示：

n == nums1.length == nums2.length
1 <= n <= 105
1 <= nums1[i], nums2[i] <= 104

思路：
转换成最大连续子序列问题

class Solution {
    public int maximumsSplicedArray(int[] nums1, int[] nums2) {
        return Math.max(deal(nums1, nums2), deal(nums2, nums1));
    }
    int deal(int[] a, int [] b) {
        int n = a.length;
        int[] d = new int[n];
        int sum = Arrays.stream(a).sum();
        for (int i = 0; i < n; i++) {
            d[i] = b[i] - a[i];
        }
        int max = 0, c = 0;
        for (int i = 0; i < n; i++) {
            c += d[i];
            if (c < 0) c = 0;
            max = Math.max(max, c);
        }
        return max + sum;
    }
}

6103. 从树中删除边的最小分数

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的最小分数。

示例 1：
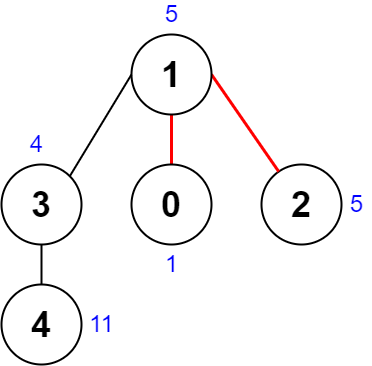
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]] 输出：9 解释：上图展示了一种删除边方案。 - 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。 - 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。 - 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。分数是最大异或值和最小异或值的差值，10 - 1 = 9 。可以证明不存在分数比 9 小的删除边方案。
示例 2：
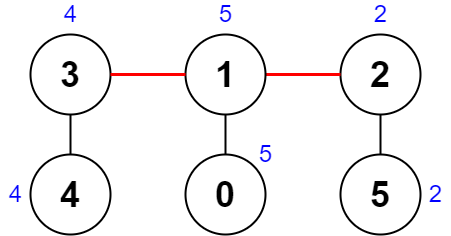
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]] 输出：0 解释：上图展示了一种删除边方案。 - 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。 - 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。 - 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。分数是最大异或值和最小异或值的差值，0 - 0 = 0 。无法获得比 0 更小的分数 0 。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 108
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树

思路：
范围只有1000考虑O(n2)的做法。
分类讨论即可

class Solution {
    int N = 1010;
    int[] h = new int[N], e = new int[2 * N], ne = new int[2 * N];
    int idx = 0;
    int[] w = new int[N];
    int n;
    int[] nums;
    Set<Integer>[] set = new HashSet[N];
    public int minimumScore(int[] nums, int[][] edges) {
        this.nums = nums;
        Arrays.fill(h, -1);
        n = nums.length;
        for (int[] p : edges) {
            int a = p[0], b = p[1];
            add(a, b);
            add(b, a);
        }
        dfs(0, -1);
        dfs2(0, -1);
        int res = 0x3f3f3f3f;
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < n; j++) {
                if (i == j) continue;
                int a = 0, b = 0, c = 0;
                if (set[i].contains(j)) {
                    a = w[i] ^ w[j];
                    b = w[j];
                    c = w[0] ^ w[i];
                } else if (set[j].contains(i)) {
                    a = w[j] ^ w[i];
                    b = w[i];
                    c = w[0] ^ w[j];
                } else {
                    a = w[i];
                    b = w[j];
                    c = w[0] ^ w[i] ^ w[j];
                }
                int max = Math.max(a, Math.max(b, c)), min = Math.min(a, Math.min(b, c));
                res = Math.min(max - min, res);
            }
        }
        return res;
    }
    Set<Integer> dfs2(int u, int pre) {
        Set<Integer> res = new HashSet<>();
        res.add(u);
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == pre) continue;
            res.addAll(dfs2(j, u));
        }
        set[u] = new HashSet<>(res);
        return res;
    }
    int dfs(int u, int pre) {
        int res = nums[u];
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == pre) continue;
            res ^= dfs(j, u);
        }
        w[u] = res;
        return res;
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}