周赛 - 😺 第 78 场力扣夜喵双周赛 - 《学习笔记》

">
5299. 找到一个数字的 K 美丽值
6067. 分割数组的方案数
6068. 毯子覆盖的最多白色砖块数
6069. 最大波动的子字符串

掉大分，不知道自己在想什么，晚上不适合打比赛，连续三次双周赛三题了。。。

5299. 找到一个数字的 K 美丽值

一个整数 num 的 k 美丽值定义为 num 中符合以下条件的 子字符串 数目：

子字符串长度为 k 。
子字符串能整除 num 。

给你整数 num 和 k ，请你返回_ _num 的 k 美丽值。
注意：

允许有前缀 0 。
0 不能整除任何值。

一个 子字符串 是一个字符串里的连续一段字符序列。

示例 1：
输入：num = 240, k = 2 输出：2 解释：以下是 num 里长度为 k 的子字符串： - “24_0” 中的 “24” ：24 能整除 240 。 - “240“ 中的 “40” ：40 能整除 240 。所以，k 美丽值为 2 。
示例 2：
输入：num = 430043, k = 2 输出：2 解释：以下是 num 里长度为 k 的子字符串： - “430043” 中的 “43” ：43 能整除 430043 。 - “430043” 中的 “30” ：30 不能整除 430043 。 - “430043” 中的 “00” ：0 不能整除 430043 。 - “430043” 中的 “04” ：4 不能整除 430043 。 - “430043_” 中的 “43” ：43 能整除 430043 。所以，k 美丽值为 2 。

提示：

1 <= num <= 109
1 <= k <= num.length （将 num 视为字符串）

思路：
模拟，注意读题
时间复杂度：O((n - k) * k), n <= 10

class Solution {
    public int divisorSubstrings(int num, int k) {
        int cnt = 0;
        char[] c = new String(num + "").toCharArray();
        int n = c.length;
        for (int i = 0; i + k <= n; i++) {
            Integer x = Integer.parseInt(new String(c, i, k));
            if (x == 0) continue;
            if (num % x == 0) cnt++;
        }
        return cnt;
    }
}

6067. 分割数组的方案数

给你一个下标从 0 开始长度为 n 的整数数组 nums 。
如果以下描述为真，那么 nums 在下标 i 处有一个 合法的分割 ：

前 i + 1 个元素的和 大于等于 剩下的 n - i - 1 个元素的和。
下标 i 的右边 至少有一个 元素，也就是说下标 i 满足 0 <= i < n - 1 。

请你返回 nums 中的 合法分割 方案数。

示例 1：
输入：nums = [10,4,-8,7] 输出：2 解释： 总共有 3 种不同的方案可以将 nums 分割成两个非空的部分： - 在下标 0 处分割 nums 。那么第一部分为 [10] ，和为 10 。第二部分为 [4,-8,7] ，和为 3 。因为 10 >= 3 ，所以 i = 0 是一个合法的分割。 - 在下标 1 处分割 nums 。那么第一部分为 [10,4] ，和为 14 。第二部分为 [-8,7] ，和为 -1 。因为 14 >= -1 ，所以 i = 1 是一个合法的分割。 - 在下标 2 处分割 nums 。那么第一部分为 [10,4,-8] ，和为 6 。第二部分为 [7] ，和为 7 。因为 6 < 7 ，所以 i = 2 不是一个合法的分割。所以 nums 中总共合法分割方案受为 2 。
示例 2：
输入：nums = [2,3,1,0] 输出：2 解释： 总共有 2 种 nums 的合法分割： - 在下标 1 处分割 nums 。那么第一部分为 [2,3] ，和为 5 。第二部分为 [1,0] ，和为 1 。因为 5 >= 1 ，所以 i = 1 是一个合法的分割。 - 在下标 2 处分割 nums 。那么第一部分为 [2,3,1] ，和为 6 。第二部分为 [0] ，和为 0 。因为 6 >= 0 ，所以 i = 2 是一个合法的分割。

提示：

2 <= nums.length <= 105
-105 <= nums[i] <= 105

思路：
前缀和
时间复杂度：O(n)
空间复杂度：O(n)

class Solution {
    public int waysToSplitArray(int[] nums) {
        int cnt = 0;
        int n = nums.length;
        long[] s = new long[n];
        s[0] = nums[0];
        for (int i = 1; i < n; i++)
            s[i] = s[i - 1] + nums[i];
        for (int i = 0; i < n - 1; i++)
            if (s[i] >= s[n - 1] - s[i])
                cnt++;
        return cnt;
    }
}

6068. 毯子覆盖的最多白色砖块数

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。
同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子。
请你返回使用这块毯子，最多可以盖住多少块瓷砖。

示例 1：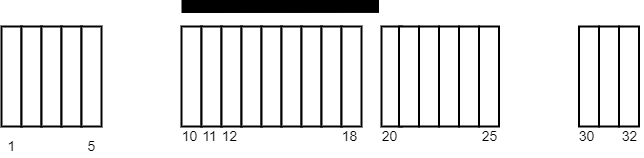

输入：tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10 输出：9 解释：将毯子从瓷砖 10 开始放置。总共覆盖 9 块瓷砖，所以返回 9 。注意可能有其他方案也可以覆盖 9 块瓷砖。可以看出，瓷砖无法覆盖超过 9 块瓷砖。
示例 2：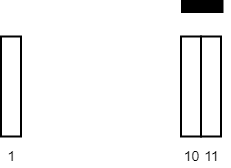

输入：tiles = [[10,11],[1,1]], carpetLen = 2 输出：2 解释：将毯子从瓷砖 10 开始放置。总共覆盖 2 块瓷砖，所以我们返回 2 。

提示：

1 <= tiles.length <= 5 * 104
tiles[i].length == 2
1 <= li <= ri <= 109
1 <= carpetLen <= 109
tiles 互相 不会重叠 。

思路：
首先注意题意，无重复，否则需要预处理一下，把它变成无重复数组后再处理
排序，然后用滑动窗口或者二分
注意细节处理
时间复杂度：O(nlogn)

// 二分
class Solution {
    public int maximumWhiteTiles(int[][] t, int c) {
        int n = t.length;
        Arrays.sort(t, (o1, o2) -> o1[0] - o2[0]);
        int max = 0;
        int[] s = new int[n];
        s[0] = t[0][1] - t[0][0] + 1;
        for (int i = 1; i < n; i++)
            s[i] = s[i - 1] + t[i][1] - t[i][0] + 1;
        for (int i = 0; i < n; i++) {
            int left = t[i][0], right = c + t[i][0] - 1;
            if (t[i][1] >= right) {
                max = c;
                break;
            }
            if (i + 1 == n || t[i + 1][0] > right) {
                max = Math.max(max, t[i][1] - t[i][0] + 1);
                continue;
            }
            int l = i + 1, r = n - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (t[mid][0] <= right)
                    l = mid;
                else
                    r = mid - 1;
            }
            int v = s[l] - (i > 0 ? s[i - 1] : 0);
            if (t[l][1] > right)
                v -= t[l][1] - right;
            max = Math.max(v, max);
        }
        return max;
    }
}

// 双指针
// 左边界开始考虑
class Solution {
    public int maximumWhiteTiles(int[][] t, int c) {
        int n = t.length;
        Arrays.sort(t, (o1, o2) -> o1[0] - o2[0]);
        int cnt = 0;
        int max = 0;
        for (int i = 0, j = 0; i < n; i++) {
            int r = t[i][0] + c - 1;
            while (j < n && t[j][0] <= r) {
                cnt += t[j][1] - t[j][0] + 1;
                j++;
            }
            int k = j - 1;
            int v = cnt - Math.max(t[k][1] - r, 0);
            max = Math.max(max, v);
            cnt -= t[i][1] - t[i][0] + 1;
        }
        return max;
    }
}
// 右边界
class Solution {
    public int maximumWhiteTiles(int[][] t, int c) {
        int n = t.length;
        Arrays.sort(t, (o1, o2) -> o1[0] - o2[0]);
        int cnt = 0;
        int max = 0;
        for (int i = 0, j = 0; i < n; i++) {
            cnt += t[i][1] - t[i][0] + 1;
            int l = t[i][1] - c + 1;
            while (t[j][1] < l) {
                cnt -= t[j][1] - t[j][0] + 1;
                j++;
            }
            int v = cnt - Math.max(0, l - t[j][0]);
            max = Math.max(max, v);
        }
        return max;
    }
}

6069. 最大波动的子字符串

字符串的波动定义为子字符串中出现次数最多的字符次数与出现次数最少的字符次数之差。
给你一个字符串 s ，它只包含小写英文字母。请你返回 s 里所有 子字符串的 最大波动 值。
子字符串 是一个字符串的一段连续字符序列。

示例 1：
输入：s = “aababbb” 输出：3 解释： 所有可能的波动值和它们对应的子字符串如以下所示： - 波动值为 0 的子字符串：”a” ，”aa” ，”ab” ，”abab” ，”aababb” ，”ba” ，”b” ，”bb” 和 “bbb” 。 - 波动值为 1 的子字符串：”aab” ，”aba” ，”abb” ，”aabab” ，”ababb” ，”aababbb” 和 “bab” 。 - 波动值为 2 的子字符串：”aaba” ，”ababbb” ，”abbb” 和 “babb” 。 - 波动值为 3 的子字符串 “babbb” 。所以，最大可能波动值为 3 。
示例 2：
输入：s = “abcde” 输出：0 解释： s 中没有字母出现超过 1 次，所以 s 中每个子字符串的波动值都是 0 。

提示：

1 <= s.length <= 104
s 只包含小写英文字母。

思路：
枚举最大和最小的字符分别是什么
将最大字符a考虑为1，最小字符b考虑为-1，其它字符考虑为0
接下来就是求最大连续子数组和的问题，但有点不同是该子数组得包含至少一个最小字符b
DP：
状态表示：
f[i][0]表示以i结尾的最大子数组的和
f[i][1]表示以i结尾的至少含一个最小字符的最大子数组和
初始化：f[0][0] = 0, f[0][1] = -1e9
状态转移：v表示i处值，取值为0, 1, -1
f[i][0] = max(f[i - 1][0] + v, v)
f[i][1] = f[i - 1][1] + v if v != -1
f[i][1] = max(f[i - 1][1] + v, f[i - 1][0] + v, v) if v == -1
取max(f[i][1]作为最终的结果

时间复杂度：_O_(_n_∣Σ∣2)

class Solution {
    public int largestVariance(String s) {
        char[] ch = s.toCharArray();
        int n = ch.length;
        int[][] f = new int[n + 1][2];
        int[] a = new int[n + 1];
        int max = 0;
        for (int i = 0; i < 26; i++) {
            char c1 = (char)(i + 'a');
            for (int j = 0; j < 26; j++) {
                if (i == j) continue;
                char c2 = (char)(j + 'a');
                Arrays.fill(a, 0);
                for (int k = 1; k <= n; k++)
                    if (ch[k - 1] == c1) a[k] = 1;
                    else if (ch[k - 1] == c2) a[k] = -1;
                for (int k = 0; k <= n; k++)
                    Arrays.fill(f[k], -0x3f3f3f3f);
                f[0][0] = 0;
                for (int k = 1; k <= n; k++) {
                    f[k][0] = Math.max(f[k - 1][0] + a[k], a[k]);
                    if (a[k] == -1) {
                        f[k][1] = Math.max(f[k - 1][1], f[k - 1][0]) + a[k];
                        f[k][1] = Math.max(f[k][1], a[k]);
                    } else {
                        f[k][1] = f[k - 1][1] + a[k];
                    }
                    max = Math.max(max, f[k][1]);
                }
            }
        }
        return max;
    }
}

// 空间优化，注意先更新f1, 再更新f0
class Solution {
    public int largestVariance(String s) {
        char[] c = s.toCharArray();
        int n = c.length;
        int max = 0;
        for (char a = 'a'; a <= 'z'; a++) {
            for (char b = 'a'; b <= 'z'; b++) {
                if (a == b) continue;
                int f0 = 0, f1 = (int)(-1e9);
                for (int i = 0; i < n; i++) {
                    int v = c[i] == a ? 1 : (c[i] == b ? -1 : 0);
                    if (v == -1) {
                        f1 = Math.max(v, Math.max(f1 + v, f0 + v));
                    } else {
                        f1 += v;
                    }
                    f0 = Math.max(f0 + v, v);
                    max = Math.max(max, f1);
                }
            }
        }
        return max;
    }
}