周赛 - 🏆 第 307 场力扣周赛 - 《学习笔记》

6152. 赢得比赛需要的最少训练时长
6166. 最大回文数字
6154. 感染二叉树需要的总时间
6155. 找出数组的第 K 大和

t4好难，不会做

6152. 赢得比赛需要的最少训练时长

你正在参加一场比赛，给你两个正整数 initialEnergy 和 initialExperience 分别表示你的初始精力和初始经验。
另给你两个下标从 0 开始的整数数组 energy 和 experience，长度均为 n 。
你将会依次对上 n 个对手。第 i 个对手的精力和经验分别用 energy[i] 和 experience[i] 表示。当你对上对手时，需要在经验和精力上都严格超过对手才能击败他们，然后在可能的情况下继续对上下一个对手。
击败第 i 个对手会使你的经验增加 experience[i]，但会将你的精力减少 energy[i] 。
在开始比赛前，你可以训练几个小时。每训练一个小时，你可以选择将增加经验增加 1 或者将精力增加 1 。
返回击败全部 n 个对手需要训练的最少小时数目。

示例 1：
输入：initialEnergy = 5, initialExperience = 3, energy = [1,4,3,2], experience = [2,6,3,1] 输出：8 解释：在 6 小时训练后，你可以将精力提高到 11 ，并且再训练 2 个小时将经验提高到 5 。按以下顺序与对手比赛： - 你的精力与经验都超过第 0 个对手，所以获胜。精力变为：11 - 1 = 10 ，经验变为：5 + 2 = 7 。 - 你的精力与经验都超过第 1 个对手，所以获胜。精力变为：10 - 4 = 6 ，经验变为：7 + 6 = 13 。 - 你的精力与经验都超过第 2 个对手，所以获胜。精力变为：6 - 3 = 3 ，经验变为：13 + 3 = 16 。 - 你的精力与经验都超过第 3 个对手，所以获胜。精力变为：3 - 2 = 1 ，经验变为：16 + 1 = 17 。在比赛前进行了 8 小时训练，所以返回 8 。可以证明不存在更小的答案。
示例 2：
输入：initialEnergy = 2, initialExperience = 4, energy = [1], experience = [3] 输出：0 解释：你不需要额外的精力和经验就可以赢得比赛，所以返回 0 。

提示：

n == energy.length == experience.length
1 <= n <= 100
1 <= initialEnergy, initialExperience, energy[i], experience[i] <= 100

思路：
贪心

class Solution {
    public int minNumberOfHours(int a, int b, int[] en, int[] ex) {
        int n = en.length;
        int sum = 0;
        for (int i = 0; i < n; i++) {
            if (a <= en[i]) {
                sum += en[i] + 1 - a;
                a = en[i] + 1;
            }
            a -= en[i];
        }
        for (int i = 0; i < n; i++) {
            if (b <= ex[i]) {
                sum += ex[i] + 1 - b;
                b = ex[i] + 1;
            }
            b += ex[i];
        }
        return sum;
    }
}

6166. 最大回文数字

给你一个仅由数字（0 - 9）组成的字符串 num 。
请你找出能够使用 num 中数字形成的 最大回文 整数，并以字符串形式返回。该整数不含 前导零 。
注意：

你无需使用 num 中的所有数字，但你必须使用至少一个数字。
数字可以重新排序。

示例 1：
输入：num = “444947137” 输出：“7449447” 解释： 从 “44494**7**_137_” 中选用数字 “4449477”，可以形成回文整数 “7449447” 。可以证明 “7449447” 是能够形成的最大回文整数。
示例 2：
输入：num = “00009” 输出：“9” 解释： 可以证明 “9” 能够形成的最大回文整数。注意返回的整数不应含前导零。

提示：

1 <= num.length <= 105
num 由数字（0 - 9）组成

思路：贪心

class Solution {
    public String largestPalindromic(String num) {
        int[] cnt = new int[10];
        for (int i = 0; i < num.length(); i++) {
            cnt[num.charAt(i) - '0']++;
        }
        StringBuilder sb = new StringBuilder();
        for (int i = 9; i > 0; i--) {
            if (cnt[i] >= 2) {
                cnt[i] -= 2;
                sb.append(i);
                break;
            }
        }
        if (sb.length() == 0) {
            for (int i = 9; i >= 0; i--) {
                if (cnt[i] > 0) {
                    sb.append(i);
                    break;
                }
            }
        } else {
            for (int i = 9; i >= 0; i--) {
                int x = cnt[i] / 2;
                cnt[i] -= x * 2;
                while (x-- > 0) sb.append(i);
            }
            boolean flag = false;
            for (int i = 9; i >= 0; i--) {
                if (cnt[i] > 0) {
                    sb.append(i);
                    flag = true;
                    break;
                }
            }
            for (int i = flag ? sb.length() - 2 : sb.length() - 1; i >= 0; i--) {
                sb.append(sb.charAt(i));
            }
        }
        return sb.toString();
    }
}

6154. 感染二叉树需要的总时间

给你一棵二叉树的根节点 root ，二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟，感染将会从值为 start 的节点开始爆发。
每分钟，如果节点满足以下全部条件，就会被感染：

节点此前还没有感染。
节点与一个已感染节点相邻。

返回感染整棵树需要的分钟数。

示例 1：
输入：root = [1,5,3,null,4,10,6,9,2], start = 3 输出：4 解释：节点按以下过程被感染： - 第 0 分钟：节点 3 - 第 1 分钟：节点 1、10、6 - 第 2 分钟：节点5 - 第 3 分钟：节点 4 - 第 4 分钟：节点 9 和 2 感染整棵树需要 4 分钟，所以返回 4 。

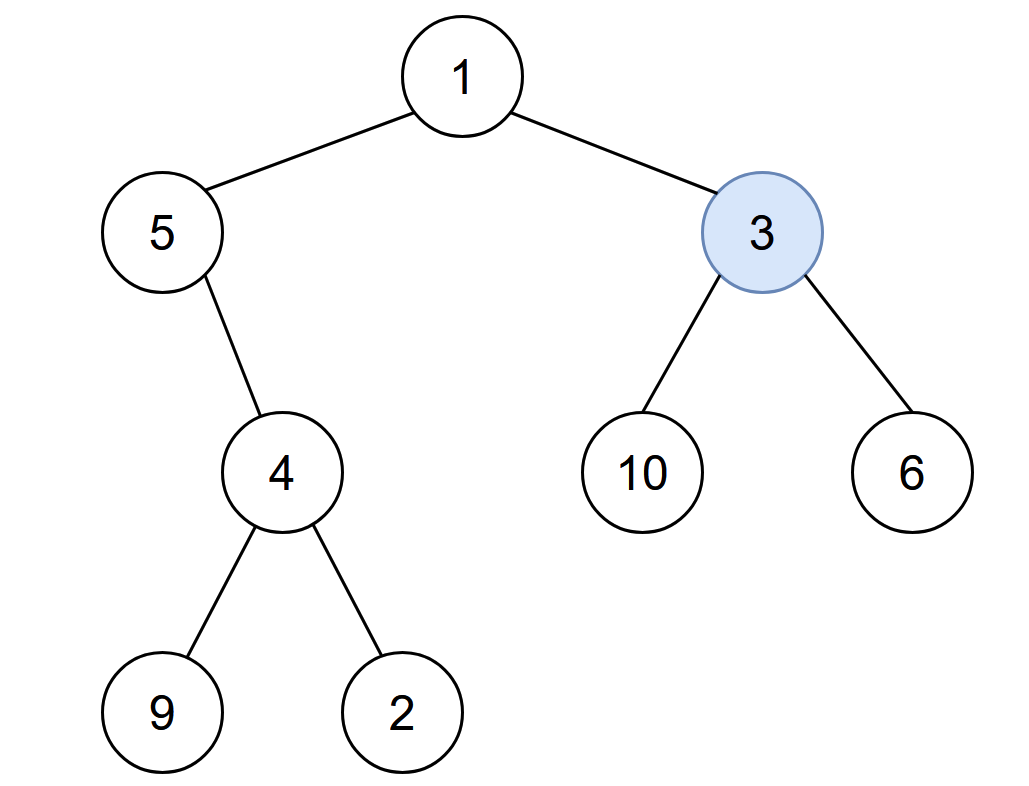
示例 2：
输入：root = [1], start = 1 输出：0 解释：第 0 分钟，树中唯一一个节点处于感染状态，返回 0 。

提示：

树中节点的数目在范围 [1, 105] 内
1 <= Node.val <= 105
每个节点的值 互不相同
树中必定存在值为 start 的节点

思路：
建图直接写

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int N = 100010;
    int[] h = new int[N], e = new int[2 * N], ne = new int[2 * N];
    int idx;
    public int amountOfTime(TreeNode root, int start) {
        Arrays.fill(h, -1);
        dfs(root);
        return dfs2(start, -1);
    }
    int dfs2(int u, int p) {
        int res = 0;
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == p) continue;
            res = Math.max(res, dfs2(j, u) + 1);
        }
        return res;
    }
    void dfs(TreeNode u) {
        if (u == null) return;
        if (u.left != null) {
            add(u.val, u.left.val);
            add(u.left.val, u.val);
            dfs(u.left);
        }
        if (u.right != null) {
            add(u.val, u.right.val);
            add(u.right.val, u.val);
            dfs(u.right);
        }
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

6155. 找出数组的第 K 大和

给你一个整数数组 nums 和一个正整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。
数组的 第 k 大和 定义为：可以获得的第 k 个最大子序列和（子序列和允许出现重复）
返回数组的 第 k 大和 。
子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。
注意：空子序列的和视作 0 。

示例 1：
输入：nums = [2,4,-2], k = 5 输出：2 解释：所有可能获得的子序列和列出如下，按递减顺序排列： - 6、4、4、2、2、0、0、-2 数组的第 5 大和是 2 。
示例 2：
输入：nums = [1,-2,3,4,-10,12], k = 16 输出：10 解释：数组的第 16 大和是 10 。

提示：

n == nums.length
1 <= n <= 105
-109 <= nums[i] <= 109
1 <= k <= min(2000, 2n)

思路：
暴力不现实
考虑如何从最大值一步步得到下一大值
正负数都有，按绝对值从小到大排序
考虑长度为1的序列，长度为2的序列，等等，用优先队列一步步得到下一个数

class Solution {
    public long kSum(int[] nums, int k) {
        long s = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] >= 0)
                s += nums[i];
            else nums[i] = -nums[i];
        }
        Arrays.sort(nums);
        PriorityQueue<Map.Entry<Long, Integer>> q = new PriorityQueue<>(
                (o1, o2) -> Long.compare(o2.getKey(), o1.getKey()));
        q.offer(Map.entry(s, -1));
        while (-- k > 0) {
            var t = q.poll();
            long x = t.getKey();
            int idx = t.getValue();
            if (idx + 1 < nums.length) {
                q.offer(Map.entry(x - nums[idx + 1], idx + 1));
                if (idx >= 0)
                    q.offer(Map.entry(x + nums[idx] - nums[idx + 1], idx + 1));
            }
        }
        return q.peek().getKey();
    }
}