字符串相关 - Trie - 《学习笔记》

字典树
例题
- 1938. 查询最大基因差">1938. 查询最大基因差

字典树

思想：相同的前缀只存储一次。
如pdf所示：
文稿 2021年7月6日.pdf

用途：

字符串统计
求数组中的元素最大异或和

例题

835. Trie字符串统计

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，输入的字符串总长度不超过 105，字符串仅包含小写英文字母。
输入格式
第一行包含整数 N，表示操作数。
接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 xx 在集合中出现的次数。
每个结果占一行。
数据范围
1≤N≤2∗104
输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

思路：用Trie树存储字符串，方便后续查询

import java.util.*;
import java.io.*;
public class Main {
    public static void main(String[] sss) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int m = Integer.parseInt(br.readLine());
        //创建根节点
        Trie root = new Trie();
        while (m-- > 0) {
            String[] str = br.readLine().split(" ");
            if (str[0].equals("I")) {
                root.add(str[1]);
            } else {
                bw.write(root.query(str[1]) + "\n");
            }
        }
        br.close();
        bw.close();
    }
}
class Trie {
    Trie[] son = new Trie[26];
    //count:以当前节点作为最终字符的字符串个数
    int count;
    void add(String str) {
        int n = str.length();
        Trie cur = this;
        for (int i = 0; i < n; i++) {
            int idx = str.charAt(i) - 'a';
            if (cur.son[idx] == null) cur.son[idx] = new Trie();
            cur = cur.son[idx];
        }
        cur.count++;
    }
    int query(String str) {
        int n = str.length();
        Trie cur = this;
        for (int i = 0; i < n; i++) {
            int idx = str.charAt(i) - 'a';
            if (cur.son[idx] == null) return 0;
            cur = cur.son[idx];
        }
        return cur.count;
    }
}

143. 最大异或对

在给定的 N 个整数 A1，A2……AN 中选出两个进行 xor（异或）运算，得到的结果最大是多少？
输入格式
第一行输入一个整数 N。
第二行输入 N个整数 A1～AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤105,
0≤Ai<231
输入样例：

3
1 2 3

输出样例：

思路：
用字典树存储每个数的二进制形式，注意从高位向低位进行，方便后续异或查找
对于数组中的每个数，查询字典树，找到最大异或值。

import java.util.*;
import java.io.*;
public class Main {
    public static void main(String[] sss) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int n = Integer.parseInt(br.readLine());
        int[] nums = new int[n];
        Trie root = new Trie();
        String[] str = br.readLine().split(" ");
        for (int i = 0; i < n; i++) nums[i] = Integer.parseInt(str[i]);
        //构造字典树
        for (int num : nums) {
            root.add(num);
        }
        //查询最大值
        int res = 0;
        for (int num : nums) {
            res = Math.max(res, root.union(num));
        }
        bw.write(Integer.toString(res));
        br.close();
        bw.close();
    }
}
class Trie {
    Trie[] son = new Trie[2];
    static final int HIGH_BIT = 30;
    void add(int num) {
        Trie cur = this;
        for (int i = HIGH_BIT; i >= 0; i--)  {
            int idx = (num >> i) & 1;
            if (cur.son[idx] == null) cur.son[idx] = new Trie();
            cur = cur.son[idx];
        }
    }
    int union(int num) {
        Trie cur = this;
        int res = 0;
        for (int i = HIGH_BIT; i >= 0; i--) {
            int idx = (num >> i) & 1;
            if (cur.son[1-idx] != null) {
                res += (1 << i);
                cur = cur.son[1-idx];
            }
            else {
                cur = cur.son[idx];
            }
        }
        return res;
    }
}

1938. 查询最大基因差

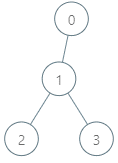
给你一棵 n 个节点的有根树，节点编号从 0 到 n - 1 。每个节点的编号表示这个节点的 独一无二的基因值 （也就是说节点 x 的基因值为 x）。两个基因值的 基因差 是两者的 异或和 。给你整数数组 parents ，其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的根，那么 parents[x] == -1 。
给你查询数组 queries ，其中 queries[i] = [nodei, vali] 。对于查询 i ，请你找到 vali 和 pi 的 最大基因差 ，其中 pi 是节点 nodei 到根之间的任意节点（包含 nodei 和根节点）。更正式的，你想要最大化 vali XOR pi 。
请你返回数组_ _ans ，其中 ans[i] 是第 i 个查询的答案。

示例 1：
输入：parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]] 输出：[2,3,7] 解释：查询数组处理如下： - [0,2]：最大基因差的对应节点为 0 ，基因差为 2 XOR 0 = 2 。 - [3,2]：最大基因差的对应节点为 1 ，基因差为 2 XOR 1 = 3 。 - [2,5]：最大基因差的对应节点为 2 ，基因差为 5 XOR 2 = 7 。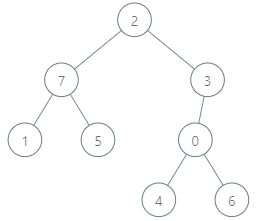

示例 2：
输入：parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]] 输出：[6,14,7] 解释：查询数组处理如下： - [4,6]：最大基因差的对应节点为 0 ，基因差为 6 XOR 0 = 6 。 - [1,15]：最大基因差的对应节点为 1 ，基因差为 15 XOR 1 = 14 。 - [0,5]：最大基因差的对应节点为 2 ，基因差为 5 XOR 2 = 7 。

提示：

2 <= parents.length <= 105
对于每个不是根节点的 i ，有 0 <= parents[i] <= parents.length - 1 。
parents[root] == -1
1 <= queries.length <= 3 * 104
0 <= nodei <= parents.length - 1
0 <= vali <= 2 * 105

思路：
离线操作 + Trie
对树进行后序遍历，每次先在字典树中添加该节点，处理完所有与该节点相同的查询后将该节点从字典树中删除。这样每次只会处理从根节点到当前节点这一个分支。
字典树也可以进行删除操作，学到了！

class Solution {
    Map<Integer, List<int[]>> map = new HashMap<>();
    int N = 100010;
    int[] h = new int[N], e = new int[N], ne = new int[N];
    int n, idx, m;
    int[] res;
    Trie trie = new Trie();
    public int[] maxGeneticDifference(int[] parents, int[][] queries) {
        n = parents.length; m = queries.length;
        res = new int[m];
        for (int i = 0; i < queries.length; i++) {
            int node = queries[i][0];
            map.computeIfAbsent(node, key->new ArrayList<>()).add(new int[]{queries[i][0], queries[i][1], i});
        }
        // System.out.println(map);
        Arrays.fill(h, -1);
        int root = 0;
        for (int i = 0; i < n; i++) {
            int a = parents[i], b = i;
            if (a != -1)
                add(a, b);
            else
                root = b;
        }
        dfs(root);
        return res;
    }
    void dfs(int u) {
        trie.insert(u);
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            dfs(j);
        }
        for (int[] p : map.getOrDefault(u, new ArrayList<>())) {
            int idx = p[2], v = p[1];
            res[idx] = trie.query(v);
        }
        trie.delete(u);
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}
class Trie {
    int OFFSET = 18;
    class TrieNode {
        TrieNode[] son = new TrieNode[2];
        int cnt;
    }
    TrieNode root = new TrieNode();
    void insert(int x) {
        TrieNode cur = root;
        for (int i = OFFSET; i >= 0; i--) {
            int v = x >> i & 1;
            if (cur.son[v] == null) {
                cur.son[v] = new TrieNode();
            }
            cur = cur.son[v];
            cur.cnt++;
        }
    }
    int query(int x) {
        TrieNode cur = root;
        int res = 0;
        for (int i = OFFSET; i >= 0; i--) {
            int v = x >> i & 1;
            if (cur.son[v^1] == null) {
                cur = cur.son[v];
            } else {
                res |= 1 << i;
                cur = cur.son[v^1];
            }
        }
        return res;
    }
    void delete(int x) {
        delete(OFFSET, x, root);
    }
    void delete(int u, int x, TrieNode cur) {
        if (u < 0) return;
        TrieNode ne = cur.son[x >> u & 1];
        delete(u - 1, x, ne);
        if (ne.cnt > 1) ne.cnt--;
        else cur.son[x >> u & 1] = null;
    }
    // 找Bug用的
    List<String> res = new ArrayList<>();
    public String toString() {
        TrieNode cur = root;
        StringBuilder sb = new StringBuilder();
        res.clear();
        get(0, cur, sb);
        return res.toString();
    }
    void get(int cnt, TrieNode cur, StringBuilder sb) {
        if (cnt > OFFSET) {
            res.add(sb.toString());
            return;
        }
        for (int i = 0; i < 2; i++) {
            if (cur.son[i] != null) {
                sb.append(i);
                get(cnt + 1, cur.son[i], sb);
                sb.deleteCharAt(sb.length() - 1);
            }
        }
    }
}