周赛 - 🏆 第 249 场力扣周赛 - 《学习笔记》

第一次参加周赛，碰到3和4都是困难，虽然我2也不会做，当时真的太菜了。

1929. 数组串联

给你一个长度为 n 的整数数组 nums 。请你构建一个长度为 2n 的答案数组 ans ，数组下标 从 0 开始计数 ，对于所有 0 <= i < n 的 i ，满足下述所有要求：

ans[i] == nums[i]
ans[i + n] == nums[i]

具体而言，ans 由两个 nums 数组串联形成。
返回数组_ _ans 。

示例 1：
输入：nums = [1,2,1] 输出：[1,2,1,1,2,1] 解释：数组 ans 按下述方式形成： - ans = [nums[0],nums[1],nums[2],nums[0],nums[1],nums[2]] - ans = [1,2,1,1,2,1]
示例 2：
输入：nums = [1,3,2,1] 输出：[1,3,2,1,1,3,2,1] 解释：数组 ans 按下述方式形成： - ans = [nums[0],nums[1],nums[2],nums[3],nums[0],nums[1],nums[2],nums[3]] - ans = [1,3,2,1,1,3,2,1]

提示：

n == nums.length
1 <= n <= 1000
1 <= nums[i] <= 1000

思路：过于简单了

1930. 长度为 3 的不同回文子序列

给你一个字符串 s ，返回 s 中 长度为 3 的不同回文子序列 的个数。
即便存在多种方法来构建相同的子序列，但相同的子序列只计数一次。
回文是正着读和反着读一样的字符串。
子序列 是由原字符串删除其中部分字符（也可以不删除）且不改变剩余字符之间相对顺序形成的一个新字符串。

例如，”ace” 是 “abcde“ 的一个子序列。

示例 1：
输入：s = “aabca” 输出：3 解释：长度为 3 的 3 个回文子序列分别是： - “aba” (“aabca“ 的子序列) - “aaa” (“aabca“ 的子序列) - “aca” (“aabca“ 的子序列)
示例 2：
输入：s = “adc” 输出：0 解释：“adc” 不存在长度为 3 的回文子序列。
示例 3：
输入：s = “bbcbaba” 输出：4 解释：长度为 3 的 4 个回文子序列分别是： - “bbb” (“bbcbaba” 的子序列) - “bcb” (“bbcbaba” 的子序列) - “bab” (“bbcbaba” 的子序列) - “aba” (“bbcbaba“ 的子序列)

提示：

3 <= s.length <= 105
s 仅由小写英文字母组成

思路：
暴力枚举复杂度为O(N3)肯定会超时
方法1：使用压缩存储 + 前缀后缀 + 位统计

class Solution {
    public int countPalindromicSubsequence(String s) {
        int n = s.length();
        int[] pre = new int[n], suf = new int[n];
        for (int i = 0; i < n; i++) {
            int idx = s.charAt(i) - 'a';
            pre[i] = i > 0 ? (pre[i - 1] | (1 << idx)) : (1 << idx);
        }
        for (int i = n - 1; i >= 0; i--) {
            int idx = s.charAt(i) - 'a';
            suf[i] = i < n - 1 ? (suf[i + 1] | (1 << idx)) : (1 << idx);
        }
        int[] cnt = new int[26];
        for (int i = 1; i + 1 < n; i++) {
            int idx = s.charAt(i) - 'a';
            cnt[idx] |= pre[i - 1] & suf[i + 1];
        }
        int res = 0;
        for (int x : cnt) {
            res += Integer.bitCount(x);
        }
        return res;
    }
}

方法2：使用双指针枚举两端的字母，时间复杂度O(|26|N)

class Solution {
    public int countPalindromicSubsequence(String s) {
        int n = s.length(), res = 0;
        for (char ch = 'a'; ch <= 'z'; ch++) {
            int i = 0, j = n - 1;
            while (i < n && s.charAt(i) != ch)
                i++;
            while (j > i && s.charAt(j) != ch)
                j--;
            if (j < i || j == i) continue;
            int cnt = 0, st = 0;
            for (int k = i + 1; k < j; k++) {
                int idx=  s.charAt(k) - 'a';
                if ((st >> idx & 1) == 0) {
                    st |= 1 << idx;
                    cnt++;
                }
            }
            res += cnt;
        }
        return res;
    }
}

1931. 用三种不同颜色为网格涂色

给你两个整数 m 和 n 。构造一个 m x n 的网格，其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足：不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大，返回对 109 + 7 取余的结果。

示例 1：
输入：m = 1, n = 1 输出：3 解释：如上图所示，存在三种可能的涂色方案。

示例 2：
输入：m = 1, n = 2 输出：6 解释：如上图所示，存在六种可能的涂色方案。
示例 3：
输入：m = 5, n = 5 输出：580986

提示：

1 <= m <= 5
1 <= n <= 1000

已经在别的地方写过题解了，见题目链接

1932. 合并多棵二叉搜索树

给你 n 个 二叉搜索树的根节点 ，存储在数组 trees 中（下标从 0 开始），对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ，且不存在值相同的两个根节点。在一步操作中，将会完成下述步骤：

选择两个 不同的 下标 i 和 j ，要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
用 trees[j] 替换 trees[i] 中的那个叶节点。
从 trees 中移除 trees[j] 。

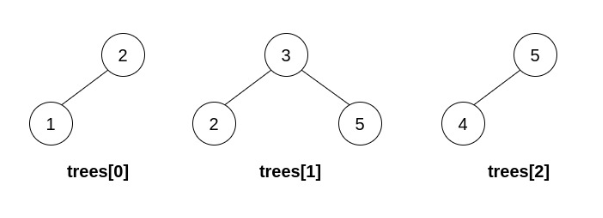
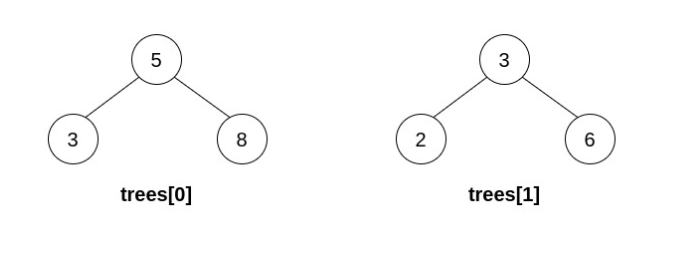
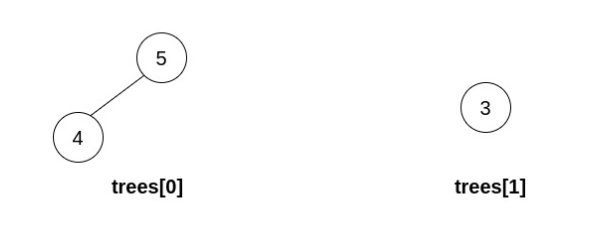
如果在执行 n - 1 次操作后，能形成一棵有效的二叉搜索树，则返回结果二叉树的 根节点 ；如果无法构造一棵有效的二叉搜索树，返回_ _null 。
二叉搜索树是一种二叉树，且树中每个节点均满足下述属性：

任意节点的左子树中的值都 严格小于 此节点的值。
任意节点的右子树中的值都 严格大于 此节点的值。

叶节点是不含子节点的节点。

示例 1：
输入：trees = [[2,1],[3,2,5],[5,4]] 输出：[3,2,5,1,null,4] 解释： 第一步操作中，选出 i=1 和 j=0 ，并将 trees[0] 合并到 trees[1] 中。删除 trees[0] ，trees = [[3,2,5,1],[5,4]] 。在第二步操作中，选出 i=0 和 j=1 ，将 trees[1] 合并到 trees[0] 中。删除 trees[1] ，trees = [[3,2,5,1,null,4]] 。结果树如上图所示，为一棵有效的二叉搜索树，所以返回该树的根节点。
示例 2：
输入：trees = [[5,3,8],[3,2,6]] 输出：[] 解释： 选出 i=0 和 j=1 ，然后将 trees[1] 合并到 trees[0] 中。删除 trees[1] ，trees = [[5,3,8,2,6]] 。结果树如上图所示。仅能执行一次有效的操作，但结果树不是一棵有效的二叉搜索树，所以返回 null 。
示例 3：
输入：trees = [[5,4],[3]] 输出：[] 解释：无法执行任何操作。
示例 4：
输入：trees = [[2,1,3]] 输出：[2,1,3] 解释：trees 中只有一棵树，且这棵树已经是一棵有效的二叉搜索树，所以返回该树的根节点。

提示：

n == trees.length
1 <= n <= 5 * 104
每棵树中节点数目在范围 [1, 3] 内。
输入数据的每个节点可能有子节点但不存在子节点的子节点
trees 中不存在两棵树根节点值相同的情况。
输入中的所有树都是 有效的二叉树搜索树 。
1 <= TreeNode.val <= 5 * 104.

思路：
从结果考虑，如果最终能构成一棵二叉搜索树，其中必然没有值相同的节点，且所有子树能凑到一棵树上。
考虑到每个子树的根节点互不相同，一定有一棵是整个树的根节点，其余子树根节点必然能插入到内部节点上，有且仅有一个位置能插入。
因此各子树的所有叶子节点的值一定互不相同(因为叶子节点最终在整个树中应该唯一出现)，且每个子树的根节点都能对应到某个叶子节点上。
有且仅有一个子树的根节点无法在所有叶子节点中找到对应的！

故代码如下

将所有子树叶节点加入集合中判断有无重复，若有直接返回null
将所有子树根节点加入到哈希表中，键为根节点的值，值为根节点
判断能否将除了根节点外的其它子树根节点的值在集合中找到一一对应的值，并记录根节点
使用队列按拓扑序造整棵树
判断树是否符合二叉搜索树的要求以及是否有子树未被加入。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode canMerge(List<TreeNode> trees) {
        int n = trees.size();
        Map<Integer, TreeNode> map = new HashMap<>();
        Set<Integer> set = new HashSet<>();
        for (TreeNode cur : trees) {
            map.put(cur.val, cur);
            if (cur.left != null) {
                if (set.contains(cur.left.val)) return null;
                set.add(cur.left.val);
            }
            if (cur.right != null) {
                if (set.contains(cur.right.val)) return null;
                set.add(cur.right.val);
            }
        }
        int cnt = 0;
        TreeNode root = null;
        for (TreeNode cur : trees) {
            if (set.contains(cur.val)) {
                cnt++;
            } else {
                root = cur;
            }
        }
        if (cnt != n - 1 || root == null) return null;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            TreeNode cur = q.poll();
            TreeNode left = cur.left, right = cur.right;
            if (left != null && map.containsKey(left.val)) {
                cur.left = map.get(left.val);
                q.offer(cur.left);
            }
            if (right != null && map.containsKey(right.val)) {
                cur.right = map.get(right.val);
                q.offer(cur.right);
            }
        }
        dfs(root);
        if (flag && count - 1 == set.size()) return root;
        return null;
    }
    boolean flag = true;
    int pre = -1, count = 0;
    void dfs(TreeNode root) {
        if (root == null)
            return;
        count++;
        dfs(root.left);
        if (root.val < pre) {
            flag = false;
            return;
        }
        pre = root.val;
        dfs(root.right);
    }
}